浙教版备考2023年中考数学一轮复习64.四边形的综合
试卷更新日期:2023-01-09 类型:一轮复习
一、单选题(每题3分,共30分)
-
1. 若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形 的两条对角线 一定是( )A、互相平分 B、互相垂直 C、互相平分且相等 D、互相垂直且相等2. 将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
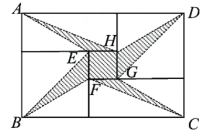 A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积3. 如图,在四边形 中,点 , , , 分别是 , , , 边上的中点,则下列结论一定正确的是( )
A、正方形纸片的面积 B、四边形EFGH的面积 C、△BEF的面积 D、△AEH的面积3. 如图,在四边形 中,点 , , , 分别是 , , , 边上的中点,则下列结论一定正确的是( )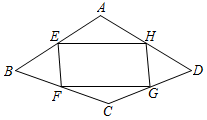 A、四边形 是矩形 B、四边形 的内角和小于四边形 的内角和 C、四边形 的周长等于四边形 的对角线长度之和 D、四边形 的面积等于四边形 面积的4. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )
A、四边形 是矩形 B、四边形 的内角和小于四边形 的内角和 C、四边形 的周长等于四边形 的对角线长度之和 D、四边形 的面积等于四边形 面积的4. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )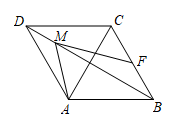 A、1 B、 C、 D、25. 如图,四边形中,E、F、G、H分别是、、、的中点,若中点四边形是菱形,那么原四边形满足什么条件( )
A、1 B、 C、 D、25. 如图,四边形中,E、F、G、H分别是、、、的中点,若中点四边形是菱形,那么原四边形满足什么条件( ) A、 B、 C、 D、6. 如图,在平面直角坐标系中,▱的顶点在反比例函数上,顶点在反比例函数上,点在轴的正半轴上,则▱的面积是( )
A、 B、 C、 D、6. 如图,在平面直角坐标系中,▱的顶点在反比例函数上,顶点在反比例函数上,点在轴的正半轴上,则▱的面积是( ) A、5 B、4 C、2 D、不确定7. 如图,在边长为a的正方形中,E是对角线上一点,且 , 点P是上一动点,则点P到边 , 的距离之和的值( )
A、5 B、4 C、2 D、不确定7. 如图,在边长为a的正方形中,E是对角线上一点,且 , 点P是上一动点,则点P到边 , 的距离之和的值( ) A、有最大值a B、有最小值 C、是定值a D、是定值8. 如图,菱形ABCD中, , , 点E,F分别是边AB,CD的中点,动点P从点E出发,按逆时针方向,沿EB,BC,CF匀速运动到点F停止,设的面积为S,动点P运动的路径总长为x,能表示S与x函数关系的图象大致是( ).
A、有最大值a B、有最小值 C、是定值a D、是定值8. 如图,菱形ABCD中, , , 点E,F分别是边AB,CD的中点,动点P从点E出发,按逆时针方向,沿EB,BC,CF匀速运动到点F停止,设的面积为S,动点P运动的路径总长为x,能表示S与x函数关系的图象大致是( ). A、
A、 B、
B、 C、
C、 D、
D、 9. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )
9. 七巧板是一种古老的中国传统智力玩具,如图,在正方形纸板ABCD中,BD为对角线,E,F分别为BC,CD的中点,分别交BD,EF于O,P两点,M,N分别为BO,DC的中点,连接AP,NF,沿图中实线剪开即可得到一副七巧板,则在剪开之前,关于该图形,下列说法:①图中的三角形都是等腰直角三角形;②四边形MPEB是菱形;③四边形PFDM的面积占正方形ABCD面积的.正确的有( )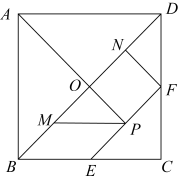 A、只有① B、①② C、①③ D、②③10. 如图,在矩形中,点E是的中点,的平分线交于点F将沿折叠,点D恰好落在上M点处,延长交于点N,有下列四个结论:①垂直平分;②是等边三角形;③;④ . 其中,正确结论的序号是( )
A、只有① B、①② C、①③ D、②③10. 如图,在矩形中,点E是的中点,的平分线交于点F将沿折叠,点D恰好落在上M点处,延长交于点N,有下列四个结论:①垂直平分;②是等边三角形;③;④ . 其中,正确结论的序号是( ) A、①②③ B、①③④ C、②③④ D、①②④
A、①②③ B、①③④ C、②③④ D、①②④二、填空题(每题4分,共24分)
-
11. 如图,正方形的边长为a,以正方形的边长a为半径向外分别作两个四分之一圆,则阴影部分的面积可表示为 . (结果保留π)
 12. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是 .
12. 利用图形的分、和、移、补探索图形关系,是我国传统数学的一种重要方法.如图1,BD是矩形ABCD的对角线,将△BCD分割成两对全等的直角三角形和一个正方形,然后按图2重新摆放,观察两图,若a=4,b=2,则矩形ABCD的面积是 . 13. 如图,两条宽度分别为2和4的长方形纸条交叉放置,重叠部分为四边形 , 若 , 则四边形的面积是
13. 如图,两条宽度分别为2和4的长方形纸条交叉放置,重叠部分为四边形 , 若 , 则四边形的面积是 14. 如图,在矩形中, . 若点E是边AD上的一个动点,过点E作且分别交对角线AC,直线BC于点O、F,则在点E移动的过程中,的最小值为 .
14. 如图,在矩形中, . 若点E是边AD上的一个动点,过点E作且分别交对角线AC,直线BC于点O、F,则在点E移动的过程中,的最小值为 .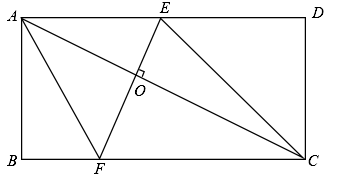 15. 如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,过D作AE的垂线,垂足为点.H,连接BH并延长,交CD于点F,连接DE交BF于点O,则下列结论:①△ABE≌△AHD;②∠AED=∠CED;③BH=FH;④CD=FH;⑤BC-CF=HE,其中正确的是 . (填序号)
15. 如图,在矩形ABCD中,AD=AB,∠BAD的平分线交BC于点E,过D作AE的垂线,垂足为点.H,连接BH并延长,交CD于点F,连接DE交BF于点O,则下列结论:①△ABE≌△AHD;②∠AED=∠CED;③BH=FH;④CD=FH;⑤BC-CF=HE,其中正确的是 . (填序号)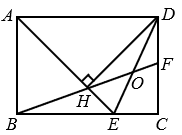 16. 如图,在矩形ABCD中, , , 点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止(同时点Q也停止),这段时间内,当运动时间为时,P、Q、C、D四点组成矩形.
16. 如图,在矩形ABCD中, , , 点P从点A向点D以每秒1cm的速度运动,Q以每秒4cm的速度从点C出发,在B、C两点之间做往返运动,两点同时出发,点P到达点D为止(同时点Q也停止),这段时间内,当运动时间为时,P、Q、C、D四点组成矩形.
三、作图题(共9分)
-
17. 如图,图①、图②、图③均是的正方形网格,小正方形的边长为1,每个小正方形的顶点称为格点,线段的端点均在格点上.只用无刻度的直尺,在给定的网格中按要求画图,所画图形的顶点均在格点上,所画图形不全等,不要求写出画法
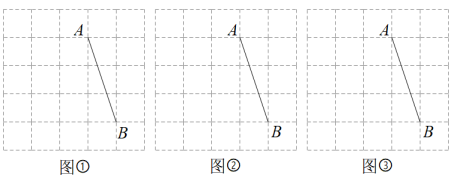 (1)、在图①中以线段为边画一个正方形 .(2)、在图②中以线段为边画一个菱形 .(3)、在图③中以A,B为顶点画一个平行四边形.
(1)、在图①中以线段为边画一个正方形 .(2)、在图②中以线段为边画一个菱形 .(3)、在图③中以A,B为顶点画一个平行四边形.四、解答题(共7题,共57分)
-
18. 如图,在平行四边形 中, ,点E为线段 的三等分点(靠近点A),点F为线段 的三等分点(靠近点C,且 .将 沿 对折, 边与 边交于点G,且 .
 (1)、证明:四边形 为矩形;(2)、求四边形 的面积.19. 定义:我们把一组对边平行另一组对边相等且不平行的四边形叫做等腰梯形 .
(1)、证明:四边形 为矩形;(2)、求四边形 的面积.19. 定义:我们把一组对边平行另一组对边相等且不平行的四边形叫做等腰梯形 . (1)、【性质初探】如图1,已知 ABCD,∠B=80°,点E是边AD上一点,连结CE,四边形ABCE恰为等腰梯形.求∠BCE的度数;(2)、【性质再探】如图2,已知四边形ABCD是矩形,以BC为一边作等腰梯形BCEF,BF=CE,连结BE、CF.求证:BE=CF;(3)、【拓展应用】如图3, ABCD的对角线AC、BD交于点O,AB=2,∠ABC=45°,过点O作AC的垂线交BC的延长线于点G,连结DG.若∠CDG=90°,求BC的长.20. 阅读理解:我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形.如图1,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)、【性质初探】如图1,已知 ABCD,∠B=80°,点E是边AD上一点,连结CE,四边形ABCE恰为等腰梯形.求∠BCE的度数;(2)、【性质再探】如图2,已知四边形ABCD是矩形,以BC为一边作等腰梯形BCEF,BF=CE,连结BE、CF.求证:BE=CF;(3)、【拓展应用】如图3, ABCD的对角线AC、BD交于点O,AB=2,∠ABC=45°,过点O作AC的垂线交BC的延长线于点G,连结DG.若∠CDG=90°,求BC的长.20. 阅读理解:我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形.如图1,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH. (1)、判断图1中的中点四边形EFGH的形状,并说明理由;(2)、当图1中的四边形ABCD的对角线添加条件时,这个中点四边形EFGH是矩形;四边形ABCD的对角线添加条件时,这个中点四边形EFGH是菱形.(3)、如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状,并证明你的结论.21. 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图, , 四边形是损矩形,则该损矩形的直径是线段 . 同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图中:和有公共边 , 在同侧有和 , 此时;再比如和有公共边 , 在同侧有和 , 此时 .
(1)、判断图1中的中点四边形EFGH的形状,并说明理由;(2)、当图1中的四边形ABCD的对角线添加条件时,这个中点四边形EFGH是矩形;四边形ABCD的对角线添加条件时,这个中点四边形EFGH是菱形.(3)、如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状,并证明你的结论.21. 定义:只有一组对角是直角的四边形叫做损矩形,连接它的两个非直角顶点的线段叫做这个损矩形的直径.如图, , 四边形是损矩形,则该损矩形的直径是线段 . 同时我们还发现损矩形中有公共边的两个三角形角的特点:在公共边的同侧的两个角是相等的.如图中:和有公共边 , 在同侧有和 , 此时;再比如和有公共边 , 在同侧有和 , 此时 . (1)、请在图中找出一对这样的角来:;(2)、如图,中, , 以为一边向外作菱形 , D为菱形对角线的交点,连接 .
(1)、请在图中找出一对这样的角来:;(2)、如图,中, , 以为一边向外作菱形 , D为菱形对角线的交点,连接 .①四边形 ▲ 损矩形(填“是”或“不是”);
②当平分时,判断四边形为何种特殊的四边形?请说明理由;
③若 , 求的长.
22. 已知,点、、、分别在正方形的边、、、上.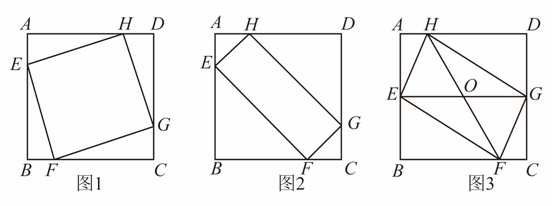 (1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.23. 问题情境
(1)、如图1,当四边形是正方形时,求证:;(2)、如图2,已知 , , 当、的大小有关系时,四边形是矩形;(3)、如图3, , 、相交于点 , , 已知正方形的边长为16,长为20,当的面积取最大值时,判断四边形是怎样的四边形?证明你的结论.23. 问题情境在综合实践课上,老师组织兴趣小组开展数学活动,探究正方形的旋转问题.在正方形和正方形中,点G,A,B在一条直线上,连接(如图1).
 (1)、操作发现
(1)、操作发现
图1中线段和的数量关系是 , 位置关系是 .(2)、在图1的基础上,将正方形绕着点A沿顺时针方向旋转,如图2所示,(1)中的结论是否成立?请仅就图2的情况说明理由.(3)、类比探究
如图3,若将图2中的正方形和正方形都变为矩形,且 , 请仅就图3的情况探究与之间的数量关系.24. 如图,平行四边形ABCD中,DB= , AB=4,AD=2,动点E,F同时从A点出发,点E沿着A→D→B的路线匀速运动,点F沿着A→B→D的路线匀速运动,当点E,F相遇时停止运动. (1)、如图1,设点E的速度为1个单位每秒,点F的速度为4个单位每秒,当运动时间为秒时,设CE与DF交于点P,求线段EP与CP长度的比值;(2)、如图2,设点E的速度为1个单位每秒,点F的速度为个单位每秒,运动时间为x秒,ΔAEF的面积为y,求y关于x的函数解析式,并指出当x为何值时,y的值最大,最大值为多少?(3)、如图3,H在线段AB上且AH=HB,M为DF的中点,当点E、F分别在线段AD、AB上运动时,探究点E、F在什么位置能使EM=HM.并说明理由.
(1)、如图1,设点E的速度为1个单位每秒,点F的速度为4个单位每秒,当运动时间为秒时,设CE与DF交于点P,求线段EP与CP长度的比值;(2)、如图2,设点E的速度为1个单位每秒,点F的速度为个单位每秒,运动时间为x秒,ΔAEF的面积为y,求y关于x的函数解析式,并指出当x为何值时,y的值最大,最大值为多少?(3)、如图3,H在线段AB上且AH=HB,M为DF的中点,当点E、F分别在线段AD、AB上运动时,探究点E、F在什么位置能使EM=HM.并说明理由.
-