(人教版)2022-2023学年七年级数学下册5.1 相交线 同步测试
试卷更新日期:2023-01-09 类型:同步测试
一、单选题
-
1. 如图所示,∠1和∠2是对顶角的是( )A、
 B、
B、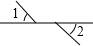 C、
C、 D、
D、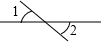 2. 如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为( )
2. 如图,直线AB、CD相交于O,且∠AOC=2∠BOC,则∠AOD的度数为( ) A、30° B、45° C、60° D、75°3. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,若∠BOD=80°,则∠BOM等于( )
A、30° B、45° C、60° D、75°3. 如图,直线AB,CD相交于点O,射线OM平分∠AOC,若∠BOD=80°,则∠BOM等于( ) A、40° B、80° C、100° D、140°4. 如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )
A、40° B、80° C、100° D、140°4. 如图,河道的同侧有、两地,现要铺设一条引水管道,从地把河水引向、两地.下列四种方案中,最节省材料的是( )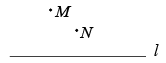 A、
A、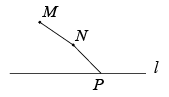 B、
B、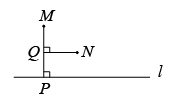 C、
C、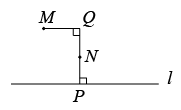 D、
D、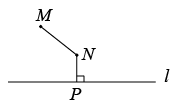 5. 点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )A、4cm B、5cm C、小于3cm D、不大于3cm6. 如图,在测量跳远成绩的示意图中,直线是起跳线,则需要测量的线段是( )
5. 点P为直线l外一点,点A、B、C为直线l上三点,PA=4cm,PB=5cm,PC=3cm,则点P到直线l的距离为( )A、4cm B、5cm C、小于3cm D、不大于3cm6. 如图,在测量跳远成绩的示意图中,直线是起跳线,则需要测量的线段是( )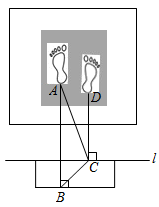 A、 B、 C、 D、7. 如图所示,在所标识的角中,内错角是( )
A、 B、 C、 D、7. 如图所示,在所标识的角中,内错角是( )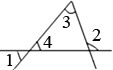 A、和 B、和 C、和 D、和8. 如图,已知两条直线被第三条直线所截,则下列说法正确的是( )
A、和 B、和 C、和 D、和8. 如图,已知两条直线被第三条直线所截,则下列说法正确的是( ) A、∠1与∠2是对顶角 B、∠2与∠5是内错角 C、∠3与∠7是同位角 D、∠3与∠8是同旁内角9. 如图,直线a,b被c所截,则与是( )
A、∠1与∠2是对顶角 B、∠2与∠5是内错角 C、∠3与∠7是同位角 D、∠3与∠8是同旁内角9. 如图,直线a,b被c所截,则与是( ) A、同位角 B、内错角 C、同旁内角 D、邻补角10. 如图,下列说法错误的是( )
A、同位角 B、内错角 C、同旁内角 D、邻补角10. 如图,下列说法错误的是( ) A、与是同位角 B、与是内错角 C、与是对顶角 D、与是同旁内角
A、与是同位角 B、与是内错角 C、与是对顶角 D、与是同旁内角二、填空题
-
11. 若与互为邻补角,且 , 则的度数为 .12. 如图,点P是直线l外一点,过点P作于点O,点A是直线l上任意一点,连接 , 若 , 则的长可能是(写出一个即可).
 13. 已知直线AB与直线CD相交于点O,∠AOC:∠BOC=2:1,射线OE⊥CD,则∠AOE的度数为 .14. 如图,直线a、b被直线c所截,则与是内错角.
13. 已知直线AB与直线CD相交于点O,∠AOC:∠BOC=2:1,射线OE⊥CD,则∠AOE的度数为 .14. 如图,直线a、b被直线c所截,则与是内错角. 15. 用吸管吸易拉罐内的饮料时,如图所示,∠1=108°,则∠2= .
15. 用吸管吸易拉罐内的饮料时,如图所示,∠1=108°,则∠2= .
三、解答题
-
16. 如图,直线AB和CD相交于点O,OA平分∠COE,∠COE:∠EOD=4:5,求∠BOD的度数.
 17. 如图,直线AB,CD相交于点O,于点O,且OF平分 , . 求和的度数.
17. 如图,直线AB,CD相交于点O,于点O,且OF平分 , . 求和的度数.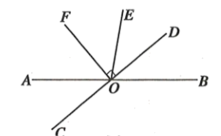 18. 如图,直线AD与AE相交于点A,直线BC分别交AD、AE于点B、C,直线DE分别交AD、AE于点D、E,分别写出图中的两对同位角、两对内错角、两对同旁内角.
18. 如图,直线AD与AE相交于点A,直线BC分别交AD、AE于点B、C,直线DE分别交AD、AE于点D、E,分别写出图中的两对同位角、两对内错角、两对同旁内角.
四、综合题
-
19. 如图,在所标注的角中.
 (1)、对顶角有对,邻补角有对;(2)、若 , , 求与的度数.20. 如图,点在直线外,点在直线上,连接 . 选择适当的工具作图.
(1)、对顶角有对,邻补角有对;(2)、若 , , 求与的度数.20. 如图,点在直线外,点在直线上,连接 . 选择适当的工具作图. (1)、在直线上作点 , 使 , 连接;(2)、在的延长线上任取一点 , 连接;(3)、在 , , 中,最短的线段是 , 依据是 .21. 已知AB∥CD,线段EF分别与AB、CD相交于点E、F.
(1)、在直线上作点 , 使 , 连接;(2)、在的延长线上任取一点 , 连接;(3)、在 , , 中,最短的线段是 , 依据是 .21. 已知AB∥CD,线段EF分别与AB、CD相交于点E、F. (1)、如图①,当∠A=20°,∠APC=70°时,求∠C的度数;(2)、如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量?试证明你的结论.
(1)、如图①,当∠A=20°,∠APC=70°时,求∠C的度数;(2)、如图②,当点P在线段EF上运动时(不包括E、F两点),∠A、∠APC与∠C之间有怎样的数量?试证明你的结论.
