重庆市南岸区2021-2022学年九年级下学期第一次定时作业数学试题
试卷更新日期:2023-01-09 类型:开学考试
一、单选题
-
1. 2021年党中央首次颁发“光荣在党50年”纪念章,约7100000名党员获此纪念章数7100000用科学记数法表示为( )A、 B、 C、 D、2. 以下是我国部分博物馆标志的图案,其中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 估算 的运算结果应在( )A、6与7之间 B、7与8之间 C、8与9之间 D、9与10之间5. 如图,已知和是以点为位似中心的位似图形,且和的位似比为1∶2,面积为2,则的面积是( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 估算 的运算结果应在( )A、6与7之间 B、7与8之间 C、8与9之间 D、9与10之间5. 如图,已知和是以点为位似中心的位似图形,且和的位似比为1∶2,面积为2,则的面积是( )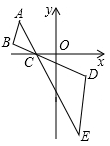 A、2 B、8 C、16 D、326. 如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.若∠C=46°,则∠AOD的度数为( )
A、2 B、8 C、16 D、326. 如图,AB是⊙O的直径,AC是⊙O的切线,A为切点,BC与⊙O交于点D,连接OD.若∠C=46°,则∠AOD的度数为( )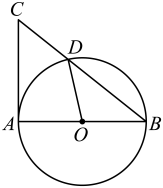 A、44° B、88° C、46° D、92°7. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 某公司上半年生产甲,乙两种型号的无人机若干架.已知甲种型号无人机架数比总架数的一半多11架,乙种型号无人机架数比总架数的三分之一少2架.设甲种型号无人机 架,乙种型号无人机 架.根据题意可列出的方程组是( )A、 B、 C、 D、9. 如图,在平行四边形ABCD中,点O是对角线AC,BD的交点, , 且 , , 则OB的长是( )
A、44° B、88° C、46° D、92°7. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、8. 某公司上半年生产甲,乙两种型号的无人机若干架.已知甲种型号无人机架数比总架数的一半多11架,乙种型号无人机架数比总架数的三分之一少2架.设甲种型号无人机 架,乙种型号无人机 架.根据题意可列出的方程组是( )A、 B、 C、 D、9. 如图,在平行四边形ABCD中,点O是对角线AC,BD的交点, , 且 , , 则OB的长是( )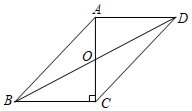 A、 B、2 C、 D、410. 甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速沿原路返回,直至与甲车相遇。在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示。下列说法错误的是( )
A、 B、2 C、 D、410. 甲、乙两车从A地出发,匀速驶向B地,甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶,乙车先到达B地并停留1h后,再以原速沿原路返回,直至与甲车相遇。在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示。下列说法错误的是( )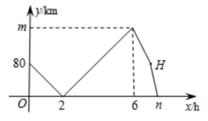 A、乙车的速度是120km/h B、m=160 C、点H的坐标是(7,80) D、n=7.511. 若数a使关于x的不等式组至少有五个整数解,关于y的分式方程的解是非负整数,则满足条件的所有整数a之和是( )A、15 B、14 C、8 D、712. 如图,在平面直角坐标中,平行四边形ABCD与y轴分别交于E、F两点,对角线BD在x轴上,反比例函数y(k≠0)的图象过点A并交AD于点G,连接DF.若BE:AE=1:2,AG:GD=3:2,且△FCD的面积为 , 则k的值是( )
A、乙车的速度是120km/h B、m=160 C、点H的坐标是(7,80) D、n=7.511. 若数a使关于x的不等式组至少有五个整数解,关于y的分式方程的解是非负整数,则满足条件的所有整数a之和是( )A、15 B、14 C、8 D、712. 如图,在平面直角坐标中,平行四边形ABCD与y轴分别交于E、F两点,对角线BD在x轴上,反比例函数y(k≠0)的图象过点A并交AD于点G,连接DF.若BE:AE=1:2,AG:GD=3:2,且△FCD的面积为 , 则k的值是( )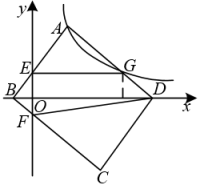 A、 B、3 C、 D、5
A、 B、3 C、 D、5二、填空题
-
13. .14. 有大小、形状、颜色完全相同的5个乒乓球,每个球上分别标有数字1、2、3、4、5中的一个,将这5个球放入不透明的袋中搅匀,如果不放回的从中随机连续抽取两个,则这两个球上的数字之和为偶数的概率是.15. 如图,矩形ABCD的边长 , , 以为直径,的中点为圆心画弧,交矩形于点D,以点A为圆心,的长为半径画弧,交于点E,则图中阴影部分的面积为 . (结果保留)
 16. 某销售商十月份销售X、Y、C三种糖果的数量之比2∶1∶1,X、Y、C三种糖果的单价之比为1∶3∶4.十一月份该销售商为了迎接双“十一”加大了宣传力度.预计三种糖果的营业额都会增加.其中X种糖果增加的营业额占总增加的营业额的 , 此时,X种糖果的营业额与十一月份三种糖果总营业颁之比为3∶8,为使十一月份Y、C两种糖果的营业额之比为2∶3,则十一月份C种糖果增加的营业额与十一月份总营业额之比为.
16. 某销售商十月份销售X、Y、C三种糖果的数量之比2∶1∶1,X、Y、C三种糖果的单价之比为1∶3∶4.十一月份该销售商为了迎接双“十一”加大了宣传力度.预计三种糖果的营业额都会增加.其中X种糖果增加的营业额占总增加的营业额的 , 此时,X种糖果的营业额与十一月份三种糖果总营业颁之比为3∶8,为使十一月份Y、C两种糖果的营业额之比为2∶3,则十一月份C种糖果增加的营业额与十一月份总营业额之比为.三、解答题
-
17. 计算:(1)、(x-y)2+x(x+3y);(2)、.18. 如图,AD是△ABC的角平分线,DE⊥AB于点E.
 (1)、用尺规完成以下基本作图:过点D作DF⊥AC于点F,连接EF交AD于点G.(不写作法,保留作图痕迹)(2)、在(1)中所作的图形中,求证:AD⊥EF.19. 近日,市委、市政府公布了第七批重庆市爱国主义教育基地名单,重庆市育才中学创办的陶行知纪念馆位列其中.如图,为了测量陶行知纪念馆的高度,小李在点处放置了高度为1.5米的测角仪 , 测得纪念馆顶端点的仰角 , 然后他沿着坡度的斜坡走了6.5米到达点 , 再沿水平方向走4米就到达了纪念馆底端点.(结果精确到0.1,参考数据: , , )
(1)、用尺规完成以下基本作图:过点D作DF⊥AC于点F,连接EF交AD于点G.(不写作法,保留作图痕迹)(2)、在(1)中所作的图形中,求证:AD⊥EF.19. 近日,市委、市政府公布了第七批重庆市爱国主义教育基地名单,重庆市育才中学创办的陶行知纪念馆位列其中.如图,为了测量陶行知纪念馆的高度,小李在点处放置了高度为1.5米的测角仪 , 测得纪念馆顶端点的仰角 , 然后他沿着坡度的斜坡走了6.5米到达点 , 再沿水平方向走4米就到达了纪念馆底端点.(结果精确到0.1,参考数据: , , )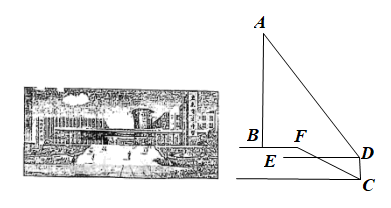 (1)、求点到纪念馆的水平距离;(2)、求纪念馆的高度约为多少米?20. “聚焦双减,落实五项管理”,为了解双减政策实施以来同学们的学习状态,某校志愿者调研了七,八年级部分同学完成作业的时间情况,从七,八年级中各抽取20名同学作业完成时间数据(单位:分钟)进行整理和分析,共分为四个时段(x表示作业完成时间,x取整数):A.;B.;C.;D. , 完成作业不超过80分钟为时间管理优秀,下面给出部分信息:
(1)、求点到纪念馆的水平距离;(2)、求纪念馆的高度约为多少米?20. “聚焦双减,落实五项管理”,为了解双减政策实施以来同学们的学习状态,某校志愿者调研了七,八年级部分同学完成作业的时间情况,从七,八年级中各抽取20名同学作业完成时间数据(单位:分钟)进行整理和分析,共分为四个时段(x表示作业完成时间,x取整数):A.;B.;C.;D. , 完成作业不超过80分钟为时间管理优秀,下面给出部分信息:七年级取20名完成作业时间:55,58,60,65,64,66,60,60,78,78,70,75,75,78,78,80,82,85,85,88.
八年级抽取20名同学中完成作业时间在C时段的所有数据为:72,75,74,76,75,75,78,75.
七,八年级抽取的同学完成作业时间统计表:
年级
平均数
中位数
众数
七年级
72
75
b
八年级
75
a
75
根据以上信息,回答下列问题:
(1)、填空: ▲ , ▲ , 并补全统计图;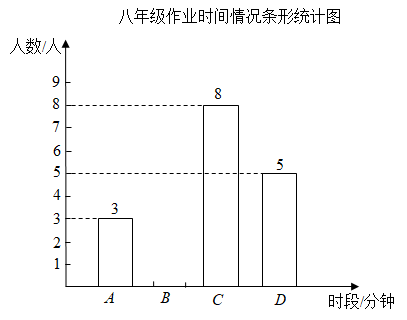 (2)、根据以上数据分析,双减政策背景的作业时间管理中,哪个年级落实得更好?请说明理由(写出一条即可);(3)、该校七年级有900人,八年级有700人,估计七、八年级为时间管理优秀的共有多少人?21. 重庆1949大剧院自建成开演以来,吸引不少外地游客前来观看,所有演出门票中,普通席和嘉宾席销售最快,已知一张普通席的票价比一张嘉宾席的票价少40元,一张普通席的票价与一张嘉宾席票价之和为600元.(1)、求普通席和嘉宾席两种门票单张票价分别为多少元?(2)、因为疫情原因,11月份以来,外地游客人数减少,普通席票平均每天售出100张,嘉宾席票平均每天售出200张.12月份后,疫情得到有效控制,观看人数明显增加,为了吸引游客,剧院决定降低普通席的票价,这样与11月份相比,普通席票平均每天售价降低金额数是售出普通席普通票增加张数的2倍,嘉宾席的票价与11月份保持不变,但平均每天售出嘉宾席票增加张数是12月份售出普通席增加张数的 , 这样12月份两种票平均一共销售总额为99200元,求12月份普通席的票价是多少元?22. 如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于点A(3,1),B(-1,n)两点.
(2)、根据以上数据分析,双减政策背景的作业时间管理中,哪个年级落实得更好?请说明理由(写出一条即可);(3)、该校七年级有900人,八年级有700人,估计七、八年级为时间管理优秀的共有多少人?21. 重庆1949大剧院自建成开演以来,吸引不少外地游客前来观看,所有演出门票中,普通席和嘉宾席销售最快,已知一张普通席的票价比一张嘉宾席的票价少40元,一张普通席的票价与一张嘉宾席票价之和为600元.(1)、求普通席和嘉宾席两种门票单张票价分别为多少元?(2)、因为疫情原因,11月份以来,外地游客人数减少,普通席票平均每天售出100张,嘉宾席票平均每天售出200张.12月份后,疫情得到有效控制,观看人数明显增加,为了吸引游客,剧院决定降低普通席的票价,这样与11月份相比,普通席票平均每天售价降低金额数是售出普通席普通票增加张数的2倍,嘉宾席的票价与11月份保持不变,但平均每天售出嘉宾席票增加张数是12月份售出普通席增加张数的 , 这样12月份两种票平均一共销售总额为99200元,求12月份普通席的票价是多少元?22. 如图,一次函数y=k1x+b的图象与反比例函数y=的图象相交于点A(3,1),B(-1,n)两点.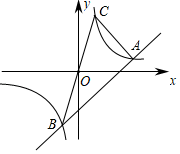 (1)、分别求出一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足k1x+b≥的x的取值范围;(3)、连接BO并延长交双曲线于点C,连接AC,求△ABC的面积.23. 一个自然数能分解成 , 其中A,B均为两位数,A的十位数字比B的十位数字少1,且A,B的个位数字之和为10,则称这个自然数为“双十数”.
(1)、分别求出一次函数和反比例函数的解析式;(2)、根据图象,直接写出满足k1x+b≥的x的取值范围;(3)、连接BO并延长交双曲线于点C,连接AC,求△ABC的面积.23. 一个自然数能分解成 , 其中A,B均为两位数,A的十位数字比B的十位数字少1,且A,B的个位数字之和为10,则称这个自然数为“双十数”.例如:∵ , 6比7小1, , ∴4819是“双十数”;
又如:∵ , 3比4小1, , ∴1496不是“双十数”.
(1)、判断297,875是否是“双十数”,并说明理由;(2)、自然数为“双十数”,N的百位及其以上的数位组成一个数记为p,N的十位数字和个位数字组成的两位数记为q,例如:∵ , ∴ , ;又如:∵ , ∴ , .若A与B的十位数字之和能被5整除,且能被比B的个位数字大10的数整除,求所有满足条件的自然数N.24. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(-1,0),B(3,0)交y轴于点C,且OC=3.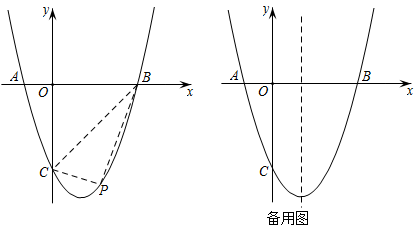 (1)、求该抛物线的解析式;(2)、点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB的面积的最大值,以及此时点P的坐标;(3)、把抛物线y=ax2+bx+c平移,使得新抛物线的顶点为(2)中求得的点P,R为新抛物线上一点,S是新抛物线对称轴上一点,直接写出所有使得以点A,C,R,S为顶点的四边形是平行四边形的点R的坐标,并把其中一个点R的坐标过程写出来.25. 在△ABC中,∠BAC=90°,AB=AC.
(1)、求该抛物线的解析式;(2)、点P为直线BC下方抛物线上的一点,连接AC、BC、CP、BP,求四边形PCAB的面积的最大值,以及此时点P的坐标;(3)、把抛物线y=ax2+bx+c平移,使得新抛物线的顶点为(2)中求得的点P,R为新抛物线上一点,S是新抛物线对称轴上一点,直接写出所有使得以点A,C,R,S为顶点的四边形是平行四边形的点R的坐标,并把其中一个点R的坐标过程写出来.25. 在△ABC中,∠BAC=90°,AB=AC.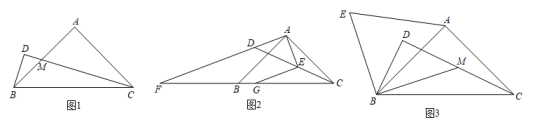 (1)、如图1,过点C作CD⊥BD交AB于M,若BM=2,tan∠DCB=.求DM的长;(2)、如图2,若AD⊥AE,且AD=AE,延长AD、CB交于点F,作EG⊥EA交CB于点G.猜想FD、CE、EG之间有何数量关系?并证明你的结论.(3)、如图3,若AB=4 , D为一动点且始终有BD⊥CD,取CD的中点M,连接BM,将MB绕点B逆时针旋转90°得到点E,直接写出△ABE面积的最大值.
(1)、如图1,过点C作CD⊥BD交AB于M,若BM=2,tan∠DCB=.求DM的长;(2)、如图2,若AD⊥AE,且AD=AE,延长AD、CB交于点F,作EG⊥EA交CB于点G.猜想FD、CE、EG之间有何数量关系?并证明你的结论.(3)、如图3,若AB=4 , D为一动点且始终有BD⊥CD,取CD的中点M,连接BM,将MB绕点B逆时针旋转90°得到点E,直接写出△ABE面积的最大值.