陕西省咸阳市泾阳县2021-2022学年八年级下学期教学衔接质量检测数学试题

试卷更新日期：2023-01-09 类型：开学考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点（0，4）的位置在（）

A、x轴正半轴上 B、第一象限 C、y轴正半轴上 D、第二象限

查看试题解析
2. 疫情期间，某中学门卫对开学提前返校的5名老师进行体温检测，记如下：36.1℃，36.3℃，36.2℃，36.3℃，36.0℃，这5名老师体温的众数是（）

A、36.0℃ B、36.1℃ C、36.2℃ D、36.3℃

查看试题解析
3. 将一次函数 $y = 2 x - 3$ 的图象沿 $y$ 轴向上平移3个单位长度后，所得图象的函数表达式为（）

A、 $y = 2 x$ B、 $y = 2 x - 6$ C、 $y = 5 x - 3$ D、 $y = - x - 3$

查看试题解析
4. 以下正方形的边长是无理数的是（）

A、面积为9的正方形 B、面积为49的正方形 C、面积为8的正方形 D、面积为64的正方形

查看试题解析
5. 如图，直线AB∥CD，CD∥EF，且∠B=30°，∠CGE=125°，则∠CGB的度数为（）

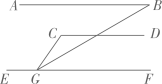A、45° B、40° C、30° D、25°

查看试题解析
6. 在正比例函数 $y = k x$ 中， $y$ 的值随着 $x$ 值的增大而增大，则一次函数 $y = k x + k$ 在平面直角象标系中的图象大致是（）

A、 B、 C、 D、

查看试题解析
7. 如图，在△ABC中，点D是AB上一点，连接CD，AC=2 $\sqrt{3}$ ，BC=2，DB=1，CD= $\sqrt{3}$ ，则AB的长为（）

A、5 B、4 C、3 D、2

查看试题解析
8. 一个长方形的周长为28厘米，长的2倍比宽的3倍多3厘米，则这个长方形的面积是（）

A、45平方厘米 B、35平方厘米 C、25平方厘米 D、20平方厘米

查看试题解析

二、填空题

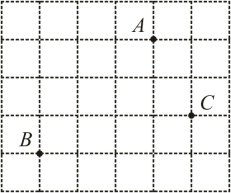
9. -27的立方根是.

查看试题解析
10. 判断命题“如果 $n < 1$ ，那么 $n^{2} - 2 < 0$ ”是假命题，只需举一个反例，则 $n$ 可以是.（只填一个值即可）

查看试题解析
11. 如图是某学校的部分平面示意图，在同一平面直角坐标系中，若体育馆 $A$ 的坐标为 $(3 ， 1)$ ，科技馆 $B$ 的坐标为 $(0 ， - 2)$ ，则教学楼 $C$ 的坐标为

查看试题解析
12. 已知关于 $x$ 、 $y$ 的二元一次方程组 ${\begin{array}{l} y = a x + b ， \\ y = - x - 2 ， \end{array}$ 的解是 ${\begin{array}{l} x = - 4 ， \\ y = m \end{array}$ ，则一次函数 $y = a x + b$ 和 $y = - x - 2$ 的图象的交点坐标为．

查看试题解析
13. 如图所示，圆柱形玻璃容器，高19cm，底面周长为30cm，在外侧下底面点 $S$ 处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口内侧距开口处1cm的点 $F$ 处有一飞蛾，急于捕获飞蛾充饥的蜘蛛，所走的最短路线的长度是cm．（玻璃容器壁厚度忽略不计）

查看试题解析

三、解答题

14. 计算： $(\sqrt{12} - \sqrt{24}) \div \sqrt{6} + | - \sqrt{50} |$

查看试题解析
15. 解方程组： ${\begin{matrix} 4 x + 3 y = 5 \\ x - 2 y = 4 \end{matrix}$ ．

查看试题解析
16. 小敏参加学校举办的“我的冬奥梦"主题演讲比赛，她的演讲稿、语言表达、形象风度得分分别为86分，80分，85分，若依次按照50%，30%，20%的百分比确定最终成绩，则她的最终成绩是多少分？

查看试题解析
17. 一艘帆船由于风向的原因先向正东方向航行了16km，然后向正北方向航行了12km，这时它离出发点有多远？

查看试题解析
18. 已知，关于 $x$ 的正比例函数 $y = (k - 1) x + k + 1$ ， $k$ 为常数.求这个正比例函数的表达式，并求出当 $x = - 4$ 时， $y$ 的值.

查看试题解析
19. 如图，在 $Δ A B C$ 中， $∠ A = 48 °$ ， $C E$ 是 $∠ A C B$ 的平分线， $B$ 、 $C$ 、 $D$ 在同一直线上， $D F / / C E$ ， $∠ D = 40 °$ ，求 $∠ B$ 的度数.

查看试题解析
20. 如图， $∠ A B C = ∠ F A C = 90 °$ ， $B C$ 长为3m， $A B$ 长为4cm， $A F$ 长为12cm.求正方形 $C D E F$ 的面积.

查看试题解析
21. 已如 $y$ 的立方根是2， $2 x - y$ 是16的算术平方根，求：

(1)、 $x$ 、 $y$ 的值；

(2)、 $x^{2} + y^{2}$ 的平方根.

查看试题解析
22. 如图，点 $E$ ， $F$ ， $G$ 分别在直线 $C D$ ， $A B$ ， $A D$ 上，已知 $∠ A = ∠ D$ ， $∠ C E B = ∠ B F G$ .

(1)、求证： $F G$ $∥$ $B E$ ；

(2)、若 $∠ D = 30$ ， $∠ B F G = 135 °$ ，求 $∠ F G D$ 的度数.

查看试题解析
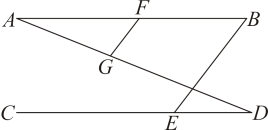23. 2021车12月13日是第八个南京大屠杀死难者国家公祭日，南京大屠杀死难者国家公祭日是为了在南京大屠杀中被日军杀害的30万无辜军民，它的设立表明中国人民反对侵略战争、捍卫人类尊严、维护世界和平的坚定立场.已知表示“勿”、“忘”、“历”、“史”的点的坐标分别为 $(3 ， 4)$ ， $(2 ， 0)$ 、 $(- 3 ， 2)$ ， $(- 2 ， 2)$ .

(1)、请在平面直角坐标系中标出这些点；

(2)、表示“吾”、“辈”的这两个点关于轴对称；

(3)、已知表示“自”、“强”的点分别与“史”，“勿”关于 $x$ 轴对称，请在图中标出这两个点.

查看试题解析
24. 中国古典诗词是中国古代文学艺术的精健，是中国文化长河里的瑰宝，它以最精炼、最抒情的文字直达人心底.近日，学校为弘扬国学文化，提升学生文学素养，特举办了一次以“漫步古诗苑”为主题的诗词竞赛，满分100分，学生得分均为整数，在初赛中，八年级甲乙两学生成绩如下（单位：分）；
甲组：70，70，70，80，90
乙组：60，70，80，80，100.
组别
平均数
中位数
方差
甲组
$m$
$a$
$n$
乙组
78
b
176

(1)、以上成绩统计分析表中 $a =$ ， $b =$ ；

(2)、如果你是八年级辅导员，选择成绩稳定的小组进入复赛，你会选择哪一组学生代表八年级进入复赛？并说明理由.

查看试题解析
25. 某快递公司每天下午15：00～16：00为集中揽件和派件时段，甲仓库用来揽收快件，乙仓库用来派发快件，快件 $y$ （件）与时间 $x$ （分）之民的函数图象如图所示.

(1)、求出甲仓库揽收与时间分之间的函数表达式：

(2)、若已知乙仓库用来蒙发快件 $y$ （件）与时间 $x$ （分）之网的函数表达式是 $y = - 4 x + 240$ $(0 < x < 60)$ ，问经过多少分钟时，甲仓库比乙仓库的快件数量密200件？此时甲仓库的位件数量是多少？

查看试题解析
26. 邻近2022午春节，四安疫情形势较为分别为300mL和500mL的甲、乙两种消毒液若干瓶，已知购买2瓶甲种和1瓶乙种消毒液需要61元.购买3瓶甲种和4瓶乙种消毒液需要154元.

(1)、求甲、乙两种毒液的单价；

(2)、为节约成本，该校购买散装消消毒液进行分装，现需将11.22L的消毒全都装入最大容量分别为300mL和500mL两种空版中（每瓶均装满），若分装时平均每瓶需损耗20mL，请问如何加分能使总损耗最小？求出此需要的两种空瓶的数列.

查看试题解析

组别	平均数	中位数	方差
甲组	$m$	$a$	$n$
乙组	78	b	176