湖北省孝感市孝南区2022-2023学年九年级上学期期末数学试卷
试卷更新日期:2023-01-09 类型:期末考试
一、单选题
-
1. 现有五张分别画有等边三角形、平行四边形、矩形、正五边形和圆的五个图形的卡片,它们的背面相同,小梅将它们的背面朝上,从中任意抽出一张,下列说法中正确的是( )A、“抽出的图形是中心对称图形”属于必然事件 B、“抽出的图形是六边形”属于随机事件 C、抽出的图形为四边形的概率是 D、抽出的图形为轴对称图形的概率是2. 如图,是的弦,半径为 , , 则弦的长为( )
 A、 B、 C、 D、3. 用配方法解方程 ,下列配方结果正确的是( ).A、 B、 C、 D、4. 如图,圆锥的侧面展开图使半径为3,圆心角为的扇形,则该圆锥的底面周长为( )
A、 B、 C、 D、3. 用配方法解方程 ,下列配方结果正确的是( ).A、 B、 C、 D、4. 如图,圆锥的侧面展开图使半径为3,圆心角为的扇形,则该圆锥的底面周长为( ) A、 B、 C、 D、5. 对于实数 定义运算“☆”如下: ,例如 ,则方程 的根的情况为( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根6. 如图,在中,是弦, , 半径为4,.则的长( )
A、 B、 C、 D、5. 对于实数 定义运算“☆”如下: ,例如 ,则方程 的根的情况为( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根6. 如图,在中,是弦, , 半径为4,.则的长( ) A、 B、 C、 D、7. 在同一平面直角坐标系中,一次函数 和二次函数 的图象大致为( )A、
A、 B、 C、 D、7. 在同一平面直角坐标系中,一次函数 和二次函数 的图象大致为( )A、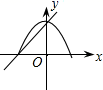 B、
B、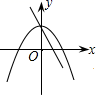 C、
C、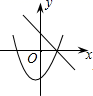 D、
D、 8. 如图,正方形 的顶点A、D在⊙O上,边 与⊙O相切,若正方形 的周长记为 ,⊙O的周长记为 ,则 、 的大小关系为( )
8. 如图,正方形 的顶点A、D在⊙O上,边 与⊙O相切,若正方形 的周长记为 ,⊙O的周长记为 ,则 、 的大小关系为( ) A、 B、 C、 D、无法判断
A、 B、 C、 D、无法判断二、填空题
-
9. 在直角坐标系中,点关于原点对称的点的坐标是 .10. 如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为 .
 11. 若二次函数 , 当时,随的增大而减小,则的取值范围是.12. 将二次函数的图像向右平移2个单位,再向上平移1个单位,所得图像的表达式是.13. 若函数y=(a+1)x2﹣2x+1的图象与x轴只有一个交点,则a为 .14. 如图是抛物线的一部分,其对称轴为直线 , 若其与x轴一交点为 , 则由图象可知,不等式的解集是 .
11. 若二次函数 , 当时,随的增大而减小,则的取值范围是.12. 将二次函数的图像向右平移2个单位,再向上平移1个单位,所得图像的表达式是.13. 若函数y=(a+1)x2﹣2x+1的图象与x轴只有一个交点,则a为 .14. 如图是抛物线的一部分,其对称轴为直线 , 若其与x轴一交点为 , 则由图象可知,不等式的解集是 .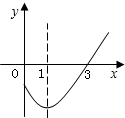 15. 当时,二次函数有最大值4,则实数m的值为 .16. 如图,正方形内接于圆O,已知正方形的边长为 , 则图中的阴影部分的面积是(用表示).
15. 当时,二次函数有最大值4,则实数m的值为 .16. 如图,正方形内接于圆O,已知正方形的边长为 , 则图中的阴影部分的面积是(用表示).
三、解答题
-
17. 解下列方程(1)、(2)、.18. 如图,点A、B的坐标分别为(0,0)、(4,0),将绕点A按逆时针方向旋转 得到.
 (1)、画出;(2)、写出点C′的坐标.19. 如图,以等边三角形ABC一边AB为直径的⊙O与边AC,BC分别交于点D,E,过点D作DF⊥BC,垂足为点F.
(1)、画出;(2)、写出点C′的坐标.19. 如图,以等边三角形ABC一边AB为直径的⊙O与边AC,BC分别交于点D,E,过点D作DF⊥BC,垂足为点F. (1)、求证:DF为⊙O的切线;(2)、若等边三角形ABC的边长为4,求DF的长;(3)、求图中阴影部分的面积.20. 已知正方形和正方形有一个公共点A,点G、E分别在线段、上.
(1)、求证:DF为⊙O的切线;(2)、若等边三角形ABC的边长为4,求DF的长;(3)、求图中阴影部分的面积.20. 已知正方形和正方形有一个公共点A,点G、E分别在线段、上. (1)、如图1, 连接、 , 若将正方形绕点A按顺时针方向旋转,判断∶“在旋转的过程中线段与的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;(2)、若将正方形绕点A按顺时针方向旋转, 连结 , 在旋转的过程中,你能否找到一条线段的长与线段的长始终相等.并以图2为例说明理由.21. 在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长米)的空地上修建一个矩形花园 , 花园的一边靠墙,另三边用总长为的栅栏围成,若设花园平行于墙的一边长为 , 花园的面积为.(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、满足条件的花园面积能达到吗?若能,求出此时x的值,若不能,说明理由;(3)、根据中求得的函数关系式,判断当x取何值时,花园的面积最大,最大面积是多少?22. 为了实现“畅通市区”的目标,市地铁一号线准备动工,市政府现对地铁一号线第标段工程进行招标,施工距离全长为米.经招标协定,该工程由甲、乙两公司承建,甲、乙两公司施工方案及报价分别为:
(1)、如图1, 连接、 , 若将正方形绕点A按顺时针方向旋转,判断∶“在旋转的过程中线段与的长始终相等.”是否正确,若正确请说明理由,若不正确请举反例说明;(2)、若将正方形绕点A按顺时针方向旋转, 连结 , 在旋转的过程中,你能否找到一条线段的长与线段的长始终相等.并以图2为例说明理由.21. 在某市开展的环境创优活动中,某居民小区要在一块靠墙(墙长米)的空地上修建一个矩形花园 , 花园的一边靠墙,另三边用总长为的栅栏围成,若设花园平行于墙的一边长为 , 花园的面积为.(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、满足条件的花园面积能达到吗?若能,求出此时x的值,若不能,说明理由;(3)、根据中求得的函数关系式,判断当x取何值时,花园的面积最大,最大面积是多少?22. 为了实现“畅通市区”的目标,市地铁一号线准备动工,市政府现对地铁一号线第标段工程进行招标,施工距离全长为米.经招标协定,该工程由甲、乙两公司承建,甲、乙两公司施工方案及报价分别为:(1)甲公司施工单价(万元/米)与施工长度x(米)之间的函数关系为 ,
(2)乙公司施工单价(万元/米)与施工长度x(米)之间的函数关系为.
(注:工程款施工单价施工长度)
(1)、如果不考虑其他因素,单独由甲公司施工,那么完成此项工程需工程款多少万元?(2)、考虑到设备和技术等因素,甲公司必须邀请乙公司联合施工,共同完成该工程.因设备共享,两公司联合施工时市政府可节省工程款万元(从工程款中扣除).
①如果设甲公司施工米 , 那么乙公司施工________米,其施工单价________万元/米,试求市政府共支付工程款P(万元)与a(米)之间的函数关系式;
②如果市政府支付的工程款为万元,那么应将多长的施工距离安排给乙公司施工?23. “五一”节期间,小明和同学一起到游乐场游玩.如图为某游乐场大型摩天轮的示意图,其半径是20m,它匀速旋转一周需要24分钟,最底部点B离地面1m.小明乘坐的车厢经过点B时开始计时. (1)、计时4分钟后小明离地面的高度是多少?(2)、在旋转一周的过程中,小明将有多长时间连续保持在离地面31m以上的空中?24. 如图,y关于x的二次函数图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以为直径作圆,圆心为C.定点E的坐标为 , 连接.
(1)、计时4分钟后小明离地面的高度是多少?(2)、在旋转一周的过程中,小明将有多长时间连续保持在离地面31m以上的空中?24. 如图,y关于x的二次函数图象的顶点为M,图象交x轴于A、B两点,交y轴正半轴于D点.以为直径作圆,圆心为C.定点E的坐标为 , 连接. (1)、写出A、B、D三点的坐标;(2)、当m为何值时M点在直线上?判定此时直线与圆的位置关系;(3)、当m变化时,用m表示的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.
(1)、写出A、B、D三点的坐标;(2)、当m为何值时M点在直线上?判定此时直线与圆的位置关系;(3)、当m变化时,用m表示的面积S,并在给出的直角坐标系中画出S关于m的函数图象的示意图.