湖北省黄石市大冶市2022-2023学年素质教育目标检测九年级上学期期末级数学试卷
试卷更新日期:2023-01-09 类型:期末考试
一、单选题
-
1. 一元二次方程 化简成一般式后,二次项系数为9,其一次项系数为( )A、1 B、-1 C、-11 D、112. 下列环保标志,既是轴对称图形,也是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、摸出的是3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球4. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
3. 不透明的袋子中装有形状、大小、质地完全相同的6个球,其中4个黑球、2个白球,从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、摸出的是3个白球 B、摸出的是3个黑球 C、摸出的是2个白球、1个黑球 D、摸出的是2个黑球、1个白球4. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )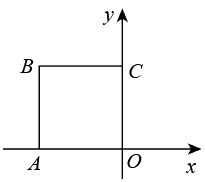 A、 B、 C、 D、5. 若关于x的方程(k-1)x 2+4x+1=0有两不相等实数根,则k的取值范围是( )A、k≤5 B、k 5 C、k≤5且k≠1 D、k<5且k≠16. 将抛物线y=x2向右平移a个单位,再向上平移b个单位得到解析式y=x2-4x+2,则a、b的值是( )A、-2,-2 B、-2,2 C、2,-2 D、2,27. 二次函数y=x2+bx+3满足当x<-2时,y随x的增大而减小,当x>-2时,y随x的增大而增大,则x=1时,y的值等于( )A、-8 B、0 C、3 D、88. 如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( )
A、 B、 C、 D、5. 若关于x的方程(k-1)x 2+4x+1=0有两不相等实数根,则k的取值范围是( )A、k≤5 B、k 5 C、k≤5且k≠1 D、k<5且k≠16. 将抛物线y=x2向右平移a个单位,再向上平移b个单位得到解析式y=x2-4x+2,则a、b的值是( )A、-2,-2 B、-2,2 C、2,-2 D、2,27. 二次函数y=x2+bx+3满足当x<-2时,y随x的增大而减小,当x>-2时,y随x的增大而增大,则x=1时,y的值等于( )A、-8 B、0 C、3 D、88. 如图,AB是⊙O的弦,且AB=6,点C是弧AB中点,点D是优弧AB上的一点,∠ADC=30°,则圆心O到弦AB的距离等于( ) A、 B、 C、 D、9. 已知点 , 在反比例函数的图象上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、10. 二次函数(a,c为常数且)经过 , 且 , 下列结论:①;②;③若关于x的方程有整数解,则符合条件的p的值有3个;④当时,二次函数的最大值为c,则.其中一定正确的有( )A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、9. 已知点 , 在反比例函数的图象上,且 , 则下列结论一定正确的是( )A、 B、 C、 D、10. 二次函数(a,c为常数且)经过 , 且 , 下列结论:①;②;③若关于x的方程有整数解,则符合条件的p的值有3个;④当时,二次函数的最大值为c,则.其中一定正确的有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若与关于原点对称,则的值为 .12. 关于 的一元二次方程 的一个根是2,则另一个根是 .13. 小亮从家到学校要经过两个设置有红绿灯的路口,第1个路口红绿灯的转换时间是:红灯60秒、绿灯30秒;第二个路口红绿灯的转换时间是:红灯50秒、绿灯50秒.路口之间红绿灯的转换互不相关,小亮上学时两次都遇到绿灯的概率是.14. 在如图所示的网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,点都是格点,若图中扇形是一个圆锥的侧面展开图,则该圆锥底面圆的半径为.
 15. 关于x的一元二次方程有两个不相等的实数根.设方程的两个实数根分别为 , , 且 , 则k的值是.16. 开口向上的抛物线过点 , , , 若 , , 三个数中有且只有一个数大于零,则a的取值范围是.17. 如图,反比例函数y= 的图象经过▱ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,▱ABCD的面积为6,则k= .
15. 关于x的一元二次方程有两个不相等的实数根.设方程的两个实数根分别为 , , 且 , 则k的值是.16. 开口向上的抛物线过点 , , , 若 , , 三个数中有且只有一个数大于零,则a的取值范围是.17. 如图,反比例函数y= 的图象经过▱ABCD对角线的交点P,已知点A,C,D在坐标轴上,BD⊥DC,▱ABCD的面积为6,则k= .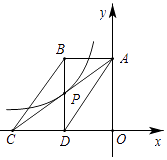 18. 如图,D是等边三角形外一点,连接 , 已知 , , 则当线段的长度最小时,① , ②的最小值是.
18. 如图,D是等边三角形外一点,连接 , 已知 , , 则当线段的长度最小时,① , ②的最小值是.
三、解答题
-
19. 解方程:(1)、3x2-10x+6=0(2)、5x(x-1)=2-2x.20. 如图,在中, , 将绕点B按逆时针方向旋转 , 得到 , 连接交于点F.
 (1)、求证:;(2)、求的度数.21. 阅读材料,解答问题:已知实数m,n满足 , , 且 , 则m,n是方程的两个不相等的实数根,由韦达定理可知 , .根据上述材料,解决以下问题:(1)、直接应用:已知实数a,b满足: , 且 , 则 , ;(2)、间接应用:在(1)条件下,求的值;(3)、拓展应用:已知实数x,y满足: , 且 , 求的值.22. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种自己最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
(1)、求证:;(2)、求的度数.21. 阅读材料,解答问题:已知实数m,n满足 , , 且 , 则m,n是方程的两个不相等的实数根,由韦达定理可知 , .根据上述材料,解决以下问题:(1)、直接应用:已知实数a,b满足: , 且 , 则 , ;(2)、间接应用:在(1)条件下,求的值;(3)、拓展应用:已知实数x,y满足: , 且 , 求的值.22. 随着信息技术的迅猛发展,人们去商场购物的支付方式更加多样、便捷.某校数学兴趣小组设计了一份调查问卷,要求每人选且只选一种自己最喜欢的支付方式.现将调查结果进行统计并绘制成如下两幅不完整的统计图,请结合图中所给的信息解答下列问题: (1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为度;(2)、将条形统计图补充完整;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.23. 某城市发生疫情,第x天新增病例y(人)如下表所示:
(1)、这次活动共调查了人;在扇形统计图中,表示“支付宝”支付的扇形圆心角的度数为度;(2)、将条形统计图补充完整;(3)、在一次购物中,小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付,请用画树状图或列表格的方法,求出两人恰好选择同一种支付方式的概率.23. 某城市发生疫情,第x天新增病例y(人)如下表所示:x
1
2
3
4
…
14
15
y
2
24
46
68
…
288
310
(1)、根据图表(y与x满足一次函数,二次函数,反比例函数中的一种),请求出y与x的函数解析式;(2)、由于疫情传染性强,第15天开始新增病例人数模型发生变化,第x天新增病例y(人)满足(m为已知数).请预计第几天新增病例清零;(3)、为应对本轮疫情,按照每一个新增病例需当天提供一张病床的要求,政府应该在哪一天为新增病例提供的病床最多?最多应该提供多少张病床?

