2023年中考数学精选真题实战测试18 平面直角坐标系B

试卷更新日期：2023-01-08 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，在△ABC中，点A（3，1），B（1，2），将△ABC向左平移2个单位，再向上平移1个单位，则点B的对应点B′的坐标为（）

A、（3，-3） B、（3，3） C、（－1，1） D、（－1，3）

查看试题解析
2. 如图是一个教室平面示意图，我们把小刚的座位“第1列第3排”记为 $(1 ， 3)$ .若小丽的座位为 $(3 ， 2)$ ，以下四个座位中，与小丽相邻且能比较方便地讨论交流的同学的座位是（）

A、 $(1 ， 3)$ B、 $(3 ， 4)$ C、 $(4 ， 2)$ D、 $(2 ， 4)$

查看试题解析
3. 点 $P (- 1 ， 2)$ 所在象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 如图所示， $A (2 \sqrt{2} ， 0)$ ， $A B = 3 \sqrt{2}$ ，以点A为圆心，AB长为半径画弧交x轴负半轴于点C，则点C的坐标为（）

A、 $(3 \sqrt{2} ， 0)$ B、 $(\sqrt{2} ， 0)$ C、 $(- \sqrt{2} ， 0)$ D、 $(- 3 \sqrt{2} ， 0)$

查看试题解析
5. 如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O重合， $A B ∥ x$ 轴，交y轴于点P.将△OAP绕点O顺时针旋转，每次旋转90°，则第2022次旋转结束时，点A的坐标为（）

A、 $(\sqrt{3} ， - 1)$ B、 $(- 1 ， - \sqrt{3})$ C、 $(- \sqrt{3} ， - 1)$ D、 $(1 ， \sqrt{3})$

查看试题解析
6. 已知坐标平面上有一直线 $L$ 与一点 $A .$ 若 $L$ 的方程式为 $x = - 2$ ， $A$ 点坐标为 $(6 ， 5)$ ，则 $A$ 点到直线 $L$ 的距离为何？（）

A、3 B、4 C、7 D、8

查看试题解析
7. 如图，点A的坐标为 $(0 ， 2)$ ，点B是x轴正半轴上的一点，将线段AB绕点A按逆时针方向旋转60°得到线段AC.若点C的坐标为 $(m ， 3)$ ，则m的值为（）

A、 $\frac{4 \sqrt{3}}{3}$ B、 $\frac{2 \sqrt{21}}{3}$ C、 $\frac{5 \sqrt{3}}{3}$ D、 $\frac{4 \sqrt{21}}{3}$

查看试题解析
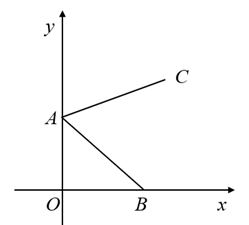8. 如图，△OAB的顶点O(0，0)，顶点A，B分别在第一、四象限，且AB⊥x轴，若AB=6，OA=OB=5，则点A的坐标是（）

A、 $(5 ， 4)$ B、 $(3 ， 4)$ C、 $(5 ， 3)$ D、 $(4 ， 3)$

查看试题解析
9. 如图， $△ A B C$ 的三个顶点都在方格纸的格点上，其中 $A$ 点的坐标是 $(- 1 ， 0)$ ，现将 $△ A B C$ 绕 $A$ 点按逆时针方向旋转 $90 °$ ，则旋转后点 $C$ 的坐标是（）

A、 $(2 ， - 3)$ B、 $(- 2 ， 3)$ C、 $(- 2 ， 2)$ D、 $(- 3 ， 2)$

查看试题解析
10. 数经历了从自然数到有理数，到实数，再到复数的发展过程，数学中把形如a+bi（a，b为实数）的数叫做复数，用z＝a+bi表示，任何一个复数z＝a+bi在平面直角坐标系中都可以用有序数对Z（a，b）表示，如：z＝1+2i表示为Z（1，2），则z＝2﹣i可表示为（）

A、Z（2，0） B、Z（2，﹣1） C、Z（2，1） D、Z（﹣1，2）

查看试题解析

二、填空题（每题4分，共24分）

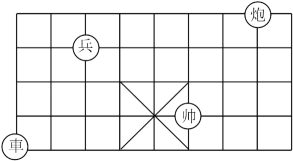
11. 观察如图所示的象棋棋盘，若“兵”所在的位置用（1，3）表示，“炮”所在的位置用（6，4）表示，那么“帅”所在的位置可表示为．

查看试题解析
12. 如图，在平面直角坐标系中，把一个点从原点开始向上平移1个单位，再向右平移1个单位，得到点 $A_{1} (1 ， 1)$ ；把点 $A_{1}$ 向上平移2个单位，再向左平移2个单位，得到点 $A_{2} (- 1 ， 3)$ ；把点 $A_{2}$ 向下平移3个单位，再向左平移3个单位，得到点 $A_{3} (- 4 ， 0)$ ；把点 $A_{3}$ 向下平移4个单位，再向右平移4个单位，得到点 $A_{4} (0 ， - 4)$ ；…；按此做法进行下去，则点 $A_{10}$ 的坐标为.

查看试题解析
13. 如图，在平面直角坐标系中，菱形 $A B C D$ 对角线的交点坐标是 $O (0 ， 0)$ ，点 $B$ 的坐标是 $(0 ， 1)$ ，且 $B C = \sqrt{5}$ ，则点 $A$ 的坐标是.

查看试题解析
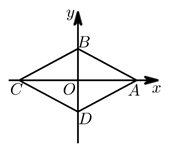14. 如图，在平面直角坐标系中， $△ A O B$ 的边 $A O ， A B$ 的中点C，D的横坐标分别是1，4，则点B的横坐标是.

查看试题解析
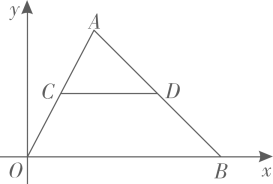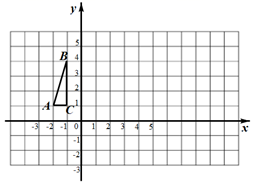15. 如图，在平面直角坐标系中，已知 $A (- 2 ， 1)$ ， $B (- 1 ， 4)$ ， $C (- 1 ， 1)$ ，将 $△ A B C$ 先向右平移3个单位长度得到 $△ A_{1} B_{1} C_{1}$ ，再绕 $C_{1}$ 顺时针方向旋转 $90 °$ 得到 $△ A_{2} B_{2} C_{1}$ ，则 $A_{2}$ 的坐标是.

查看试题解析
16. 如图，在平面直角坐标系中，点C的坐标为 $(- 1 ， 0)$ ，点A的坐标为 $(- 3 ， 3)$ ，将点A绕点C顺时针旋转 $90 °$ 得到点B，则点B的坐标为.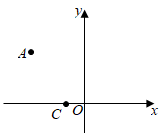

查看试题解析

三、解答题（共8题，共72分）

17. 如图，图中的小方格都是边长为1的正方形， $△ A B C$ 在方格纸中的位置如图所示，已知点 $A (- 2 ， 2)$ ， $B (- 3 ， - 1)$ ．

(1)、请在方格纸中建立平面直角坐标系，画出 $x$ 轴， $y$ 轴的位置，并写出点 $C$ 的坐标；

(2)、请在图中作出 $△ A B C$ 关于y轴对称的图形 $△ A^{'} B^{'} C^{'}$ ；

(3)、写出 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标．

查看试题解析
18. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣1，1），B（﹣4，0），C（﹣2，2），将△ABC绕原点O顺时针旋转90°后得到△A₁B₁C₁ ．

(1)、请写出A₁、B₁、C₁三点的坐标：
A₁ ， B₁ ， C₁；

(2)、求点B旋转到点B₁的弧长．

查看试题解析
19. 三角形 $A B C$ 与三角形 $A^{'} B^{'} C^{'}$ 在平面直角坐标系中的位置如图所示：

(1)、分别写出下列各点的坐标： $A$ ， $A^{'}$ ；

(2)、若点 $P (x ， y)$ 是三角形 $A B C$ 内部一点，则三角形 $A^{'} B^{'} C^{'}$ 内部的对应点 $P^{'}$ 的坐标．

(3)、三角形 $A^{'} B^{'} C^{'}$ 是由三角形 $A B C$ 经过怎样的平移得到的？

查看试题解析
20. 如图，已知线段 $a$ ，点 $A$ 在平面直角坐标系 $x O y$ 内，

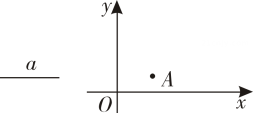(1)、用直尺和圆规在第一象限内作出点 $P$ ，使点 $P$ 到两坐标轴的距离相等，且与点 $A$ 的距离等于 $a$ .（保留作图痕迹，不写作法）

(2)、在（1）的条件下，若 $a \approx 2 \sqrt{5}$ ， $A$ 点的坐标为 $(3 ， 1)$ ，求 $P$ 点的坐标.

查看试题解析
21. 如图，在直角坐标系中， $△ A B C$ 的位置如图所示，请回答下列问题：

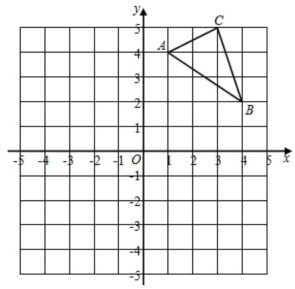(1)、请直接写出A、B、C三点的坐标、、.

(2)、画出 $△ A B C$ 关于x轴的对称图形 $△ A_{1} B_{1} C_{1}$ .

(3)、 $△ A B C$ 的面积为.

(4)、在x轴上找到一点P，使 $△ A B P$ 的周长最小，直接写出这个周长的最小值：.

查看试题解析
22. 如图，在平面直角坐标系中， $△ A O B$ 的顶点O是坐标原点，点A的坐标为 $（ 4 ， 4 ）$ ，点B的坐标为 $（ 6 ， 0 ）$ ，动点P从O开始以每秒1个单位长度的速度沿y轴正方向运动，设运动的时间为t秒（ $0 < t < 4$ ），过点P作 $P N / x$ 轴，分别交 $A O ， A B$ 于点M，N.

(1)、填空： $A O$ 的长为， $A B$ 的长为

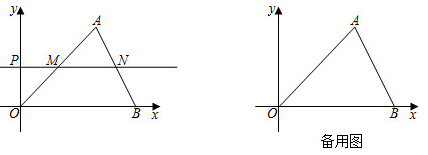(2)、当 $t = 1$ 时，求点N的坐标：

(3)、请直接写出 $M N$ 的长为（用含t的代数式表示）；

(4)、点 $E$ 是线段 $M N$ 上一动点（点E不与点 $M ， N$ 重合）， $△ A O E$ 和 $△ A B E$ 的面积分别表示为 $S_{1}$ 和 $S_{2}$ ，当 $t = \frac{4}{3}$ 时，请直接写出 $S_{1} \cdot S_{2}$ （即 $S_{1}$ 与 $S_{2}$ 的积）的最大值为.

查看试题解析
23. 如图，在平面直角坐标系中，矩形 $A B C D$ 的边 $A B$ 长是方程 $x^{2} - 3 x - 18 = 0$ 的根，连接 $B D$ ， $∠ D B C = 30 °$ ，并过点 $C$ 作 $C N ⊥ B D$ ，垂足为 $N$ ，动点P从点B以每秒2个单位长度的速度沿 $B D$ 方向匀速运动到点D为止；点M沿线段 $D A$ 以每秒 $\sqrt{3}$ 个单位长度的速度由点D向点A匀速运动，到点A为止，点P与点M同时出发，设运动时间为t秒 $(t > 0)$

(1)、线段 $C N =$ ；

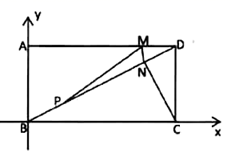(2)、连接 $P M$ 和 $M N$ ，求 $Δ P M N$ 的面积s与运动时间 $t$ 的函数关系式；

(3)、在整个运动过程中，当 $Δ P M N$ 是以 $P N$ 为腰的等腰三角形时，直接写出点P的坐标．

查看试题解析
24. 如图①，在四边形 $A B C D$ 中， $∠ B = ∠ C = 90 °$ ，点E是边 $B C$ 上一点， $A B = E C$ ， $B E = C D$ ，连接 $A E$ ， $D E$ ，可知，此时 $△ A E D$ 是等腰直角三角形；

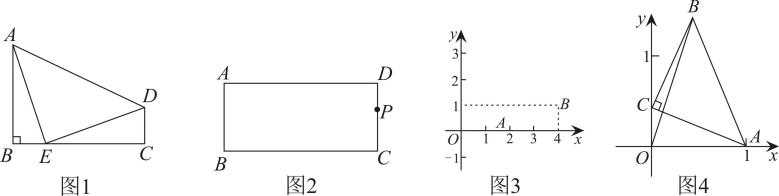(1)、【问题提出】
如图②，在长方形 $A B C D$ 中，点P是边 $C D$ 上一点，在边 $B C 、 A D$ 上分别作出点E、F，使得点F、E、P是一个等腰直角三角形的三个顶点，且 $P E = P F$ ， $∠ E P F = 90 °$
要求：用尺规作图，保留作图痕迹，不写作法；

(2)、【问题探究】
如图③，在平面直角坐标系 $x O y$ 中，已知点 $A (2 ， 0)$ ，点 $B (4 ， 1)$ ，点C在第一象限内，若 $△ A B C$ 是等腰直角三角形，求点C的坐标；

(3)、【问题解决】
如图④，在平面直角坐标系 $x O y$ 中，已知点 $A (1 ， 0)$ ，点C是y轴上的动点， $△ A B C$ 是以点C为直角顶点的等腰直角三角形，连接 $B O$ ，求 $B O + B A$ 的最小值．[注：在平面直角坐标系内， $A (a ， c)$ ， $B (b ， d)$ ，则 $A B = \sqrt{{(a - b)}^{2} + {(c - d)}^{2}}$ ]

查看试题解析