2023年中考数学精选真题实战测试17 平面直角坐标系A
试卷更新日期:2023-01-08 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 在平面直角坐标系中,点P(﹣3,a2+1)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 若点在第一象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 如图是城市某区域的示意图,建立平面直角坐标系后,学校和体育场的坐标分别是(3,1),(4,-2),下列各地点中,离原点最近的是( )
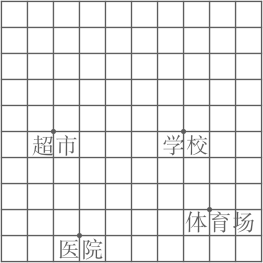 A、超市 B、医院 C、体育场 D、学校4. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
A、超市 B、医院 C、体育场 D、学校4. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )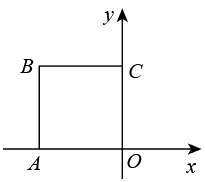 A、 B、 C、 D、5. 两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( )
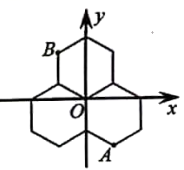
A、 B、 C、 D、5. 两个小伙伴拿着如图的密码表玩听声音猜动物的游戏,若听到“咚咚-咚咚,咚-咚,咚咚咚-咚”表示的动物是“狗”,则听到“咚咚-咚,咚咚咚-咚咚,咚-咚咚咚”时,表示的动物是( ) A、狐狸 B、猫 C、蜜蜂 D、牛6. 如图,在平面直角坐标系中,将边长为2的正六边形绕点顺时针旋转个 , 得到正六边形 , 当时,正六边形的顶点的坐标是( )
A、狐狸 B、猫 C、蜜蜂 D、牛6. 如图,在平面直角坐标系中,将边长为2的正六边形绕点顺时针旋转个 , 得到正六边形 , 当时,正六边形的顶点的坐标是( ) A、 B、 C、 D、7. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、8. 如图,在矩形中, , 则D的坐标为( )
A、 B、 C、 D、7. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、8. 如图,在矩形中, , 则D的坐标为( ) A、 B、 C、 D、9. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
A、 B、 C、 D、9. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )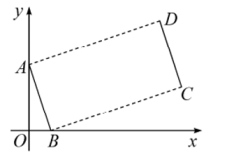 A、 B、 C、 D、10. 已知点 在第一象限,且 ,点 在 轴上,当 为直角三角形时,点 的坐标为( )A、 , 或 B、 , 或 C、 , 或 D、 , 或
A、 B、 C、 D、10. 已知点 在第一象限,且 ,点 在 轴上,当 为直角三角形时,点 的坐标为( )A、 , 或 B、 , 或 C、 , 或 D、 , 或二、解答题(共8题,共72分)
-
11. 如图,的顶点都在平面直角坐标系中的坐标轴上,的面积 , , , 求三个顶点的坐标.
 12. 若点 的坐标为( , ),其中 满足不等式组 ,
12. 若点 的坐标为( , ),其中 满足不等式组 ,求点 所在的象限.
13. 在平面直角坐标系中,点 , 点 .(1)、若点A在第一象限的角平分线上,求a的值;(2)、若点A与点B关于x轴对称,求的值.14. 在一个不透明的口袋里装有分别标有数字﹣2,﹣1,0,3的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.(1)、从中任取一球,将球上的数字记为a,求关于x的一元二次方程ax2﹣2ax+a+2=0有实数根的概率.(2)、从中任取一球,将球上的数字作为点的横坐标记为x(不放回),再任取一球,将球上的数字作为点的纵坐标,记为y,用树状图或列表法表示出点(x,y)所有可能出现的结果,并求点(x,y)落在第二象限内的概率.15. 如图,平面直角坐标系中,已知点 , , , 是 的边 上任意一点, 经过平移后得到 , 点 的对应点为 . (1)、直接写出点 , , 的坐标.(2)、在图中画出 .(3)、写出 的面积.16. 已知一次函数y=kx+b的图象经过点(-2,-4),且与正比例函数y=x的图象相交于点(4,a).(1)、求a的值;(2)、求k,b的值;(3)、求这两个函数的图象及y轴围成的三角形的面积.17. 通过对下面数学模型的研究学习,解决下列问题:
(1)、直接写出点 , , 的坐标.(2)、在图中画出 .(3)、写出 的面积.16. 已知一次函数y=kx+b的图象经过点(-2,-4),且与正比例函数y=x的图象相交于点(4,a).(1)、求a的值;(2)、求k,b的值;(3)、求这两个函数的图象及y轴围成的三角形的面积.17. 通过对下面数学模型的研究学习,解决下列问题: (1)、【模型呈现】
(1)、【模型呈现】如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC= , BC= . 我们把这个数学模型称为“K字”模型或“一线三等角”模型;
(2)、【模型应用】如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.求证:点G是DE的中点;
(3)、如图3,在平面直角坐标系xOy中,点A的坐标为(2,6),点B为平面内任一点.若△AOB是以OA为斜边的等腰直角三角形,请直接写出点B的坐标.18. 如图, 的顶点坐标分别为 ,动点P、Q同时从点O出发,分别沿x轴正方向和y轴正方向运动,速度分别为每秒3个单位和每秒2个单位,点P到达点B时点P、Q同时停止运动.过点Q作 分别交 、 于点M、N,连接 、 .设运动时间为t(秒).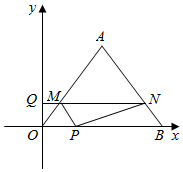 (1)、求点M的坐标(用含t的式子表示);(2)、求四边形 面积的最大值或最小值;(3)、是否存在这样的直线l,总能平分四边形 的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;(4)、连接 ,当 时,求点N到 的距离.
(1)、求点M的坐标(用含t的式子表示);(2)、求四边形 面积的最大值或最小值;(3)、是否存在这样的直线l,总能平分四边形 的面积?如果存在,请求出直线l的解析式;如果不存在,请说明理由;(4)、连接 ,当 时,求点N到 的距离.三、填空题(每空3分,共18分)
-
19. 如图,小刚在兰州市平面地图的部分区域建立了平面直角坐标系,如果白塔山公园的坐标是(2,2),中山桥的坐标是(3,0),那么黄河母亲像的坐标是 .
 20. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .
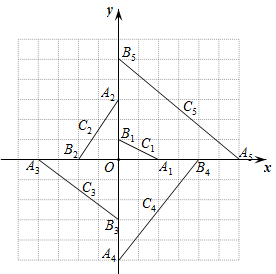
20. 如图,点的坐标是(0,3),将沿轴向右平移至 , 点的对应点E恰好落在直线上,则点移动的距离是 .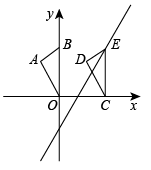 21. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .
21. 如图,在平面直角坐标系中, , , 的中点为; , , 的中点为; , , 的中点为; , , 的中点为;…;按此做法进行下去,则点的坐标为 .