2023年中考数学精选真题实战测试15一元二次方程 A

试卷更新日期：2023-01-08 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 对于实数 $a$ ， $b$ 定义新运算： $a ※ b = a b^{2} - b$ ，若关于 $x$ 的方程 $1 ※ x = k$ 有两个不相等的实数根，则 $k$ 的取值范围（）

A、 $k > - \frac{1}{4}$ B、 $k < - \frac{1}{4}$ C、 $k > - \frac{1}{4}$ 且 $k \neq 0$ D、 $k \geq - \frac{1}{4}$ 且 $k \neq 0$

查看试题解析
2. 定义新运算 $a * b$ ：对于任意实数 $a$ ， $b$ 满足 $a * b = (a + b) (a - b) - 1$ ，其中等式右边是通常的加法、减法、乘法运算，例如 $3 * 2 = (3 + 2) (3 - 2) - 1 = 5 - 1 = 4$ ．若 $x * k = 2 x$ （ $k$ 为实数）是关于 $x$ 的方程，则它的根的情况是（）

A、有一个实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根

查看试题解析
3. 受国际油价影响，今年我国汽油价格总体呈上升趋势．某地92号汽油价格三月底是6.2元/升，五月底是8.9元/升．设该地92号汽油价格这两个月平均每月的增长率为 $x$ ，根据题意列出方程，正确的是（）

A、 $6.2 (1 + x)^{2} = 8.9$ B、 $8.9 (1 + x)^{2} = 6.2$ C、 $6.2 (1 + x^{2}) = 8.9$ D、 $6.2 (1 + x) + 6.2 (1 + x)^{2} = 8.9$

查看试题解析
4. 用配方法解一元二次方程 $3 x^{2} + 6 x - 1 = 0$ 时，将它化为 ${(x + a)}^{2} = b$ 的形式，则a+b的值为（）

A、 $\frac{10}{3}$ B、 $\frac{7}{3}$ C、2 D、 $\frac{4}{3}$

查看试题解析
5. 若关于x的一元二次方程 $x^{2} - 2 m x + m^{2} - 4 m - 1 = 0$ 有两个实数根 $x_{1}$ ， $x_{2}$ ，且 $(x_{1} + 2) (x_{2} + 2) - 2 x_{1} x_{2} = 17$ ，则 $m =$ （）

A、2或6 B、2或8 C、2 D、6

查看试题解析
6. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} - x - 2022 = 0$ 的两个实数根，则代数式 $x_{1}^{3} - 2022 x_{1} + x_{2}^{2}$ 的值是（）

A、4045 B、4044 C、2022 D、1

查看试题解析
7. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - a = 0$ 的两根分别记为 $x_{1}$ ， $x_{2}$ ，若 $x_{1} = - 1$ ，则 $a - x_{1}^{2} - x_{2}^{2}$ 的值为（）

A、7 B、-7 C、6 D、-6

查看试题解析
8. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛，单循环比赛共进行了45场，共有多少支队伍参加比赛？（）

A、8 B、10 C、7 D、9

查看试题解析
9. 已知 $m$ 、 $n$ 是一元二次方程 $x^{2} + 2 x - 5 = 0$ 的两个根，则 $m^{2} + m n + 2 m$ 的值为（）

A、0 B、-10 C、3 D、10

查看试题解析
10. 某校八年级组织一次篮球赛，各班均组队参赛，赛制为单循环形式（每两班之间都赛一场），共需安排15场比赛，则八年级班级的个数为（）

A、5 B、6 C、7 D、8

查看试题解析

二、填空题每空3分，共18分）

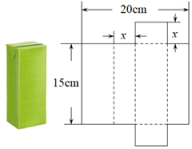
11. 将一个容积为360cm³的包装盒剪开铺平，纸样如图所示．利用容积列出图中x（cm）满足的一元二次方程：（不必化简）．

查看试题解析
12. $α$ 、 $β$ 是关于 $x$ 的方程 $x^{2} - x + k - 1 = 0$ 的两个实数根，且 $α^{2} - 2 α - β = 4$ ，则 $k$ 的值为．

查看试题解析
13. 若实数a、b分别满足a²﹣4a+3＝0，b²﹣4b+3＝0，且a≠b，则 $\frac{1}{a} + \frac{1}{b}$ 的值为 .

查看试题解析
14. 关于x的一元二次方程2x²+4mx+m=0有两个不同的实数根x₁ ， x₂ ，且 $x_{1}^{2} + x_{2}^{2} = \frac{3}{16}$ ，则m= ．

查看试题解析
15. 已知x₁、x₂是关于x的方程x²﹣2x+k﹣1＝0的两实数根，且 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$ ＝x₁²+2x₂﹣1，则k的值为 .

查看试题解析
16. 如图，小明同学用一张长11cm，宽7cm的矩形纸板制作一个底面积为 $21 c m^{2}$ 的无盖长方体纸盒，他将纸板的四个角各剪去一个同样大小的正方形，将四周向上折叠即可（损耗不计）．设剪去的正方形边长为xcm，则可列出关于x的方程为．

查看试题解析

三、解答题（共8题，共72分）

17. 解方程： $(2 x + 3)^{2} = (3 x + 2)^{2}$

查看试题解析
18. 解方程：2x²﹣x﹣3=0．

查看试题解析
19.

(1)、a，b两个实数在数轴上的对应点如图所示.
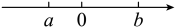
用“<”或“>”填空：ab，ab0；

(2)、在初中阶段我们已经学习了一元二次方程的三种解法，他们分别是配方法、公式法和因式分解法，请从下列一元二次方程中任选两个，并解这两个方程.
①x²+2x−1=0；②x²−3x=0；③x²−4x=4；④x²−4=0.

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} - 2 x - 3 m^{2} = 0$ .

(1)、求证：方程总有两个不相等的实数根；

(2)、若方程的两个实数根分别为 $α$ ， $β$ ，且 $α + 2 β = 5$ ，求 $m$ 的值.

查看试题解析
21. 某商店购进了一种消毒用品，进价为每件8元，在销售过程中发现，每天的销售量y（件）与每件售价x（元）之间存在一次函数关系（其中8≤x≤15，且x为整数）．当每件消毒用品售价为9元时，每天的销售量为105件；当每件消毒用品售价为11元时，每天的销售量为95件．

(1)、求y与x之间的函数关系式．

(2)、若该商店销售这种消毒用品每天获得425元的利润，则每件消毒用品的售价为多少元？

(3)、设该商店销售这种消毒用品每天获利w（元），当每件消毒用品的售价为多少元时，每天的销售利润最大？最大利润是多少元？

查看试题解析
22. 2022北京冬奥会期间，某网店直接从工厂购进A、B两款冰嫩墩钥匙扣，进货价和销售价如下表：（注：利润=销售价-进货价）
类别
价格
A款钥匙扣
B款钥匙扣
进货价（元/件）
30
25
销售价（元/件）
45
37

(1)、网店第一次用850元购进A、B两款钥匙扣共30件，求两款钥匙扣分别购进的件数；

(2)、第一次购进的冰墩嫩钥匙扣售完后，该网店计划再次购进A、B两款冰墩墩钥匙扣共80件（进货价和销售价都不变），且进货总价不高于2200元.应如何设计进货方案，才能获得最大销售利润，最大销售利润是多少？

(3)、冬奥会临近结束时，网店打算把B款钥匙扣调价销售.如果按照原价销售，平均每天可售4件.经调查发现，每降价1元，平均每天可多售2件，将销售价定为每件多少元时，才能使B款钥匙扣平均每天销售利润为90元？

查看试题解析
23. 阅读材料，解答问题：
材料1

为了解方程 ${(x^{2})}^{2} - 13 x^{2} + 36 = 0$ ，如果我们把 $x^{2}$ 看作一个整体，然后设 $y = x^{2}$ ，则原方程可化为 $y^{2} - 13 y + 36 = 0$ ，经过运算，原方程的解为 $x_{1 ， 2} = \pm 2$ ， $x_{3 ， 4} = \pm 3$ ．我们把以上这种解决问题的方法通常叫做换元法．

材料2

已知实数m，n满足 $m^{2} - m - 1 = 0$ ， $n^{2} - n - 1 = 0$ ，且 $m \neq n$ ，显然m，n是方程 $x^{2} - x - 1 = 0$ 的两个不相等的实数根，由书达定理可知 $m + n = 1$ ， $m n = - 1$ ．

根据上述材料，解决以下问题：

(1)、直接应用：
方程 $x^{4} - 5 x^{2} + 6 = 0$ 的解为；

(2)、间接应用：
已知实数a，b满足： $2 a^{4} - 7 a^{2} + 1 = 0$ ， $2 b^{4} - 7 b^{2} + 1 = 0$ 且 $a \neq b$ ，求 $a^{4} + b^{4}$ 的值；

(3)、拓展应用：
已知实数m，n满足： $\frac{1}{m^{4}} + \frac{1}{m^{2}} = 7$ ， $n^{2} - n = 7$ 且 $n > 0$ ，求 $\frac{1}{m^{4}} + n^{2}$ 的值．

查看试题解析
24. 阅读材料：
材料1：若关于x的一元二次方程ax²＋bx＋c＝0（a≠0）的两个根为x₁ ， x₂ ，则x₁＋x₂＝ $- \frac{b}{a}$ ，x₁x₂＝ $\frac{c}{a}$

材料2：已知一元二次方程x²－x－1＝0的两个实数根分别为m，n，求m²n＋mn²的值．

解：∵一元二次方程x²－x－1＝0的两个实数根分别为m，n，

∴m＋n＝1，mn＝－1，

则m²n＋mn²＝mn（m＋n）＝－1×1＝－1

根据上述材料，结合你所学的知识，完成下列问题：

(1)、材料理解：一元二次方程2x²－3x－1＝0的两个根为x₁ ， x₂ ，则x₁＋x₂＝；x₁x₂＝．

(2)、类比应用：已知一元二次方程2x²－3x－1＝0的两根分别为m、n，求 $\frac{n}{m} + \frac{m}{n}$ 的值．

(3)、思维拓展：已知实数s、t满足2s²－3s－1＝0，2t²－3t－1＝0，且s≠t，求 $\frac{1}{s} - \frac{1}{t}$ 的值．

查看试题解析