2023年中考数学精选真题实战测试16一元二次方程 B

试卷更新日期：2023-01-08 类型：二轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 关于x的方程 $x^{2} - 3 k x - 2 = 0$ 实数根的情况，下列判断正确的是（）

A、有两个相等实数根 B、有两个不相等实数根 C、没有实数根 D、有一个实数根

查看试题解析
2. 若关于 $x$ 的一元二次方程 $a x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则 $a$ 的取值范围是（）

A、 $a \neq 0$ B、 $a > - 1$ 且 $a \neq 0$ C、 $a \geq - 1$ 且 $a \neq 0$ D、 $a > - 1$

查看试题解析
3. 临近春节的三个月，某干果店迎来了销售旺季，第一个月的销售额为8万元，第三个月的销售额为11.52万元，设这两个月销售额的月平均增长率为x，则根据题意，可列方程为（）

A、 $8 (1 + 2 x) = 11.52$ B、 $2 \times 8 (1 + x) = 11.52$ C、 $8 (1 + x)^{2} = 11.52$ D、 $8 (1 + x^{2}) = 11.52$

查看试题解析
4. 已知m为方程x²+3x﹣2022＝0的根，那么m³+2m²﹣2025m+2022的值为（）

A、﹣2022 B、0 C、2022 D、4044

查看试题解析
5. 已知关于x的一元二次方程 $a x^{2} - 4 x - 1 = 0$ 有两个不相等的实数根，则a的取值范围是（）

A、 $a \geq - 4$ B、 $a > - 4$ C、 $a \geq - 4$ 且 $a \neq 0$ D、 $a > - 4$ 且 $a \neq 0$

查看试题解析
6. 定义新运算“※”：对于实数m，n，p，q，有 $[m ， p] ※ [q ， n] = m n + p q$ ，其中等式右边是通常的加法和乘法运算，如： $[2 ， 3] ※ [4 ， 5] = 2 \times 5 + 3 \times 4 = 22$ .若关于x的方程 $[x^{2} + 1 ， x] ※ [5 - 2 k ， k] = 0$ 有两个实数根，则k的取值范围是（）

A、 $k < \frac{5}{4}$ 且 $k \neq 0$ B、 $k \leq \frac{5}{4}$ C、 $k \leq \frac{5}{4}$ 且 $k \neq 0$ D、 $k \geq \frac{5}{4}$

查看试题解析
7. 已知 $a$ ， $b$ 是方程 $x^{2} - 3 x - 5 = 0$ 的两根，则代数式 $2 a^{3} - 6 a^{2} + b^{2} + 7 b + 1$ 的值是（）

A、-25 B、-24 C、35 D、36

查看试题解析
8. 一元二次方程 $x^{2} - 8 x - 2 = 0$ ，配方后可形为（）

A、 ${(x - 4)}^{2} = 18$ B、 ${(x - 4)}^{2} = 14$ C、 ${(x - 8)}^{2} = 64$ D、 ${(x - 4)}^{2} = 1$

查看试题解析
9. 已知关于x的一元二次方程： $x^{2} - 2 x + m = 0$ 有两个不相等的实数根 $x_{1}$ ， $x_{2}$ ，则（）

A、 $x_{1} + x_{2} < 0$ B、 $x_{1} x_{2} < 0$ C、 $x_{1} x_{2} > - 1$ D、 $x_{1} x_{2} < 1$

查看试题解析
10. 宾馆有50间房供游客居住，当毎间房毎天定价为180元时，宾馆会住满；当毎间房毎天的定价每增加10元时，就会空闲一间房．如果有游客居住，宾馆需对居住的毎间房毎天支出20元的费用．当房价定为多少元时，宾馆当天的利润为10890元？设房价定为x元．则有（）

A、（180+x﹣20）（50﹣ $\frac{x}{10}$ ）=10890 B、（x﹣20）（50﹣ $\frac{x - 180}{10}$ ）=10890 C、x（50﹣ $\frac{x - 180}{10}$ ）﹣50×20=10890 D、（x+180）（50﹣ $\frac{x}{10}$ ）﹣50×20=10890

查看试题解析

二、填空题每空3分，共18分）

11. 若关于 $x$ 的一元二次方程 $m x^{2} + n x - 1 = 0 (m \neq 0)$ 的一个解是 $x = 1$ ，则 $m + n$ 的值是.

查看试题解析
12. 对于任意实数a、b，定义一种运算： $a \otimes b = a^{2} + b^{2} - a b$ ，若 $x \otimes (x - 1) = 3$ ，则x的值为.

查看试题解析
13. 设 $x_{1}$ 与 $x_{2}$ 为一元二次方程 $\frac{1}{2} x^{2} + 3 x + 2 = 0$ 的两根，则 ${(x_{1} - x_{2})}^{2}$ 的值为．

查看试题解析
14. 已知实数a、b满足a－b²＝4，则代数式a²－3b²＋a－14的最小值是．

查看试题解析
15. 已知关于 $x$ 的方程 $x^{2} - (k + 4) x + 4 k = 0$ （ $k \neq 0$ ）的两实数根为 $x_{1}$ ， $x_{2}$ ，若 $\frac{2}{x_{1}} + \frac{2}{x_{2}} = 3$ ，则 $k =$ .

查看试题解析
16. 劳动教育己纳入人才培养全过程，某学校加大投入，建设校园农场，该农场一种作物的产量两年内从300千克增加到363千克.设平均每年增产的百分率为 $x$ ，则可列方程为.

查看试题解析

三、解答题（共9题，共72分）

17. 解方程：2x²﹣x﹣3=0．

查看试题解析
18. 解方程：3x（x﹣2）=x﹣2．

查看试题解析
19. 先化简，再求值：（x﹣1）÷（ $\frac{2}{x + 1}$ ﹣1），其中x为方程x²+3x+2=0的根．

查看试题解析
20. 阅读下列问题与提示后，将解方程的过程补充完整，求出x的值.
问题：解方程 $x^{2} + 2 x + 4 \sqrt{x^{2} + 2 x} - 5 = 0$ （提示：可以用换元法解方程），

解：设 $\sqrt{x^{2} + 2 x} = t (t \geq 0)$ ，则有 $x^{2} + 2 x = t^{2}$ ，

原方程可化为： $t^{2} + 4 t - 5 = 0$ ，

续解：

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} - (2 k + 1) x + k^{2} + k = 0$ .

(1)、求证：无论k取何值，方程都有两个不相等的实数根.

(2)、如果方程的两个实数根为 $x_{1}$ ， $x_{2}$ ，且k与 $\frac{x_{1}}{x_{2}}$ 都为整数，求k所有可能的值.

查看试题解析
22. 已知关于x的方程 $x^{2} - 4 x + k + 1 = 0$ 有两实数根.

(1)、求k的取值范围；

(2)、设方程两实数根分别为 $x_{1}$ 、 $x_{2}$ ，且 $\frac{3}{x_{1}} + \frac{3}{x_{2}} = x_{1} x_{2} - 4$ ，求实数k的值.

查看试题解析
23. 某工厂生产并销售A ， B两种型号车床共14台，生产并销售1台A型车床可以获利10万元；如果生产并销售不超过4台B型车床，则每台B型车床可以获利17万元，如果超出4台B型车床，则每超出1台，每台B型车床获利将均减少1万元．设生产并销售B型车床 $x$ 台．

(1)、当 $x > 4$ 时，完成以下两个问题：
①请补全下面的表格：

A型

B型

车床数量/台

▲

$x$

每台车床获利/万元

10

▲

②若生产并销售B型车床比生产并销售A型车床获得的利润多70万元，问：生产并销售B型车床多少台？

(2)、当0＜ $x$ ≤14时，设生产并销售A ， B两种型号车床获得的总利润为W万元，如何分配生产并销售A ， B两种车床的数量，使获得的总利润W最大？并求出最大利润．

查看试题解析
24. 某服装批发市场销售一种衬衫，衬衫每件进货价为50元，规定每件售价不低于进货价，经市场调查，每月的销售量 $y$ （件）与每件的售价 $x$ （元）满足一次函数关系，部分数据如下表：

售价 $x$ （元/件）

60

65

70

销售量 $y$ （件）

1400

1300

1200

(1)、求出 $y$ 与 $x$ 之间的函数表达式；（不需要求自变量 $x$ 的取值范围）

(2)、该批发市场每月想从这种衬衫销售中获利24000元，又想尽量给客户实惠，该如何给这种衬衫定价？

(3)、物价部门规定，该衬衫的每件利润不允许高于进货价的30%，设这种衬衫每月的总利润为 $w$ （元），那么售价定为多少元可获得最大利润？最大利润是多少？

查看试题解析
25. 探究：是否存在一个新矩形，使其周长和面积为原矩形的2倍、 $\frac{1}{2}$ 倍、k倍．

(1)、若该矩形为正方形，是否存在一个正方形，使其周长和面积都为边长为2的正方形的2倍？（填“存在”或“不存在”）．

(2)、继续探究，是否存在一个矩形，使其周长和面积都为长为3，宽为2的矩形的2倍？
同学们有以下思路：

①设新矩形长和宽为x、y ，则依题意 $x + y = 10$ ， $x y = 12$ ，

联立 ${\begin{array}{l} x + y = 10 \\ x y = 12 \end{array}$ 得 $x^{2} - 10 x + 12 = 0$ ，再探究根的情况：

根据此方法，请你探究是否存在一个矩形，使其周长和面积都为原矩形的 $\frac{1}{2}$ 倍；

②如图也可用反比例函数与一次函数证明 $l_{1}$ ： $y = - x + 10$ ， $l_{2}$ ： $y = \frac{12}{x}$ ，那么，

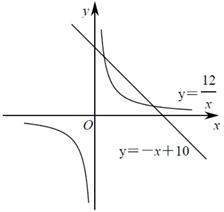
a ．是否存在一个新矩形为原矩形周长和面积的2倍？

b ．请探究是否有一新矩形周长和面积为原矩形的 $\frac{1}{2}$ ，若存在，用图像表达；

c ．请直接写出当结论成立时k的取值范围：．

查看试题解析

	A型	B型
车床数量/台	▲	$x$
每台车床获利/万元	10	▲

售价 $x$ （元/件）	60	65	70
销售量 $y$ （件）	1400	1300	1200