辽宁省大连市2022-2023学年高一上学期数学期末试卷

试卷更新日期：2023-01-07 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {1 ， 2 ， 3 ， 4}$ ，集合 $B = {x | (x + 1) (x - 3) < 0}$ ，则 $A ∩ B =$ （）

A、 ${- 1 ， 0 ， 1 ， 2 ， 3}$ B、 ${1 ， 2 ， 3}$ C、 ${1 ， 2}$ D、 ${2}$

查看试题解析
2. 已知向量 $\vec{a} = (1 ， 2)$ ， $\vec{b} = (x ， - 4)$ ，且 $\vec{a} / / \vec{b}$ ，则实数 $x =$ （）

A、2 B、1 C、 $- 1$ D、 $- 2$

查看试题解析
3. 若 $x_{1}$ ， $x_{2}$ ， …， $x_{10}$ 的方差为2，则 $3 x_{1} + 1$ ， $3 x_{2} + 1$ ， …， $3 x_{10} + 1$ 的方差是（）

A、18 B、7 C、6 D、2

查看试题解析
4. 中国共产党第二十次全国代表大会于2022年10月16日在北京开幕．党的二十大报告鼓舞人心，内涵丰富．某学校党支部评选了5份优秀学习报告心得体会（其中教师2份，学生3份），现从中随机抽选2份参展，则参展的优秀学习报告心得体会中，学生、教师各一份的概率是（）

A、 $\frac{1}{20}$ B、 $\frac{3}{5}$ C、 $\frac{3}{10}$ D、 $\frac{9}{10}$

查看试题解析
5. 下列函数中，其图像如图所示的函数为（）

A、 $y = x^{- \frac{1}{3}}$ B、 $y = x^{\frac{2}{3}}$ C、 $y = x^{\frac{1}{3}}$ D、 $y = x^{- \frac{2}{3}}$

查看试题解析
6. “北溪”管道泄漏事件的爆发，使得欧洲能源供应危机成为举世瞩目的国际公共事件．随着管道泄漏，大量天然气泄漏使得超过8万吨类似甲烷的气体扩散到海洋和大气中，将对全球气候产生灾难性影响．假设海水中某种环境污染物含量P（单位： $m g / L$ ）与时间t（单位：天）间的关系为： $P = P_{0} \cdot e^{- k t}$ ，其中 $P_{0}$ 表示初始含量，k为正常数．令 $μ = | \frac{P_{2} - P_{1}}{t_{2} - t_{1}} |$ 为 $[t_{1} ， t_{2}]$ 之间海水稀释效率，其中 $P_{1}$ ， $P_{2}$ 分别表示当时间为 $t_{1}$ 和 $t_{2}$ 时的污染物含量．某研究团队连续20天不间断监测海水中该种环境污染物含量，按照5天一期进行记录，共分为四期，即 $(0 ， 5]$ ， $(5 ， 10]$ ， $(10 ， 15]$ ， $(15 ， 20]$ 分别记为Ⅰ期，Ⅱ期，Ⅲ期，Ⅳ期，则下列哪个时期的稀释效率最高（）．

A、Ⅰ期 B、Ⅲ期 C、Ⅲ期 D、Ⅳ期

查看试题解析
7. 已知 $x > 0$ ， $y > 0$ ，且满足 $x + 2 y - x y = 0$ ，则 $\frac{9}{2 x + y}$ 的最大值为（）

A、9 B、6 C、4 D、1

查看试题解析
8. 已知定义域为D的函数 $f (x)$ ，若 $\forall x_{1} \in D$ ，都 $\exists x_{2} \in D$ ，满足 $\frac{x_{1} + f (x_{2})}{2} = a$ ，则称函数 $f (x)$ 具有性质 $P (a)$ ．若函数 $f (x)$ 具有性质 $P (1)$ ，则“ $f (x)$ 存在零点”是“ $2 \in D$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析

二、多选题

9. 十六世纪中叶，英国数学家雷科德在《砺智石》一书中首先把“＝”作为等号使用，后来英国数学家哈利奥特首次使用“＜”和“＞”符号，不等号的引入对不等式的发展影响深远．若a，b， $c \in R$ ，则下列命题正确的是（）

A、若 $a b \neq 0$ 且 $a < b$ ，则 $\frac{1}{a} > \frac{1}{b}$ B、若 $a > b$ ， $0 < c < 1$ ，则 $c^{a} < c^{b}$ C、若 $a > b > 1$ ， $c > 1$ ，则 $l o g_{a} c < l o g_{b} c$ D、若 $a < b < - 1$ ， $c > 0$ ，则 ${(\frac{a}{b})}^{c} > {(\frac{b}{a})}^{c}$

查看试题解析
10. 同时掷红、蓝两枚质地均匀的骰子，事件A表示“两枚骰子的点数之和为5”，事件B表示“红色骰子的点数是偶数”，事件C表示“两枚骰子的点数相同”，事件D表示“至少一枚骰子的点数是奇数”，则（）

A、A与C互斥 B、B与D对立 C、A与 $\bar{D}$ 相互独立 D、B与C相互独立

查看试题解析
11. 已知点P为 $△ A B C$ 所在平面内一点，且 $\vec{P A} + 2 \vec{P B} + 3 \vec{P C} = \vec{0}$ ，若E为AC的中点，F为BC的中点，则下列结论正确的是（）

A、向量 $\vec{P A}$ 与 $\vec{P C}$ 可能平行 B、点P在线段EF上 C、 $| \vec{P E} | ： | \vec{P F} | = 2 ： 1$ D、 $S_{△ P A B} ： S_{△ P A C} ： S_{△ P B C} = 1 ： 2 ： 3$

查看试题解析
12. 已知函数 $f_{1} (x) = x^{2} + 3 x - 5 (x > 0)$ ， $f_{2} (x) = e^{2 x} + x - 2$ ， $f_{3} (x) = l n x + 2 x - 4$ 的零点分别为 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ，则下列结论正确的是（）

A、 $x_{1} < x_{2} < x_{3}$ B、 $x_{2} + x_{3} = 2$ C、 $f_{3} (x_{1}) < 0$ D、 $f_{3} (x_{2}) = f_{2} (x_{3})$

查看试题解析

三、填空题

13. $2^{l o g_{2} 5} + l o g_{2} 4 =$ ．

查看试题解析
14. 已知向量 $\vec{a}$ ， $\vec{b}$ 满足 $\vec{a} = (- 1 ， 2)$ ， $\vec{b} = (x ， 1)$ ， $| \vec{a} + \vec{b} | = 3$ ，则实数 $x =$ ．

查看试题解析
15. 在考察某中学的学生身高时，采用分层抽样的方法抽取男生24人，女生16人，得到了男生的平均身高是170cm，女生的平均身高是165cm，则估计该校全体学生的平均身高是cm．

查看试题解析
16. 函数 $f (x) = (4 - x^{2}) (x^{2} + a x + b)$ 满足： $\forall x \in R$ ，都有 $f (x - 2022) = f (2024 - x)$ ，则函数 $f (x)$ 的最大值为．

查看试题解析

四、解答题

17. 如图所示，在 $△ A B C$ 中，D为BC边上一点，且 $\vec{B D} = 2 \vec{D C}$ ．过D点的直线EF与直线AB相交于E点，与直线AC相交于F点（E，F两点不重合）．

(1)、用 $\vec{A B}$ ， $\vec{A C}$ 表示 $\vec{A D}$ ；

(2)、若 $\vec{A E} = λ \vec{A B}$ ， $\vec{A F} = μ \vec{A C}$ ，求 $\frac{1}{λ} + \frac{2}{μ}$ 的值．

查看试题解析
18. 已知集合 $A = {x | - 1 \leq x \leq 3}$ ，集合 $B = {x | m - 2 \leq x \leq m + 2 ， m \in R}$ ．

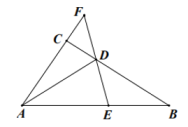(1)、若 $A \cap B = {x | 0 \leq x \leq 3}$ ，求实数 $m$ 的值；

(2)、若 $p ： x \in A$ ， $q ： x \in ∁_{R} B$ ，且p是q的充分条件，求实数 $m$ 的取值范围．

查看试题解析
19. 近年来，“直播带货”受到越来越多人的喜爱，目前已经成为推动消费的一种流行的营销形式．某直播平台800个直播商家，对其进行调查统计，发现所售商品多为小吃、衣帽、生鲜、玩具、饰品类等，各类直播商家所占比例如图1所示．

(1)、该直播平台为了更好地服务买卖双方，打算随机抽取40个直播商家进行问询交流．如果按照分层抽样的方式抽取，则应抽取小吃类、玩具类商家各多少家？

(2)、在问询了解直播商家的利润状况时，工作人员对抽取的40个商家的平均日利润进行了统计（单位：元），所得频率分布直方图如图2所示．请根据频率分布直方图计算下面的问题；
（ⅰ）估计该直播平台商家平均日利润的中位数与平均数（结果保留一位小数，求平均数时同一组中的数据用该组区间的中点值作代表）；
（ⅱ）若将平均日利润超过420元的商家成为“优秀商家”，估计该直播平台“优秀商家”的个数．

查看试题解析
20. 第56届世界乒乓球团体锦标赛于2022年在中国成都举办，国球运动又一次掀起热潮．现有甲乙两人进行乒乓球比赛，比赛采用7局4胜制，每局11分制，每赢一球得1分，选手只要得到至少11分，并且领先对方至少2分（包括2分），即赢得该局比赛．在一局比赛中，每人只发2个球就要交换发球权，如果双方比分为10：10后，每人发一个球就要交换发球权．

(1)、已知在本场比赛中，前三局甲赢两局，乙赢一局，在后续比赛中，每局比赛甲获胜的概率为 $\frac{3}{5}$ ，乙获胜的概率为 $\frac{2}{5}$ ，且每局比赛的结果相互独立，求甲乙两人只需要再进行两局比赛就能结束本场比赛的概率；

(2)、已知某局比赛中双方比分为8：8，且接下来两球由甲发球，若甲发球时甲得分的概率为 $\frac{2}{3}$ ，乙发球时乙得分的概率为 $\frac{1}{2}$ ，各球的结果相互独立，求该局比赛甲得11分获胜的概率．

查看试题解析
21. 已知函数 $f (x) = \frac{b}{4^{x} + a} + 1$ 的定义域为R，其图像关于点 $(\frac{1}{2} ， \frac{1}{2})$ 对称．

(1)、求实数a，b的值；

(2)、求 $f (\frac{1}{2023}) + f (\frac{2}{2023}) + ⋯ + f (\frac{2022}{2023})$ 的值；

(3)、若函数 $g (x) = f (x + \frac{1}{2}) + l o g_{4} \frac{2 + x}{2 - x}$ ，判断函数 $g (x)$ 的单调性（不必写出证明过程），并解关于t的不等式 $g (2 t - 1) + g (t + 2) > 1$ ．

查看试题解析
22. 已知函数 $f (x)$ 的图像与函数 $g (x) = 3^{x} - 1$ 的图像关于直线 $y = x$ 对称，函数 $h (x) = l o g_{9} (| x - a | + 1)$ ．

(1)、若 $a = 4$ ，求 $F (x) = f (x) \cdot h (x)$ 在 $x \in [0 ， 4]$ 上的最大值；

(2)、设 $H (x) = m a x {f (x) ， 2 h (x)}$ ， $x \in [0 ， 4]$ ，求 $H (x)$ 的最小值，其中 $m a x {a ， b} = {\begin{array}{l} a ， a \geq b \\ b ， a < b \end{array}$ ．

查看试题解析