福建省厦门市2022-2023学年高一上学期期末教学质量检测
试卷更新日期:2023-01-07 类型:期末考试
一、单选题
-
1. 若集合是与的公倍数, , , 且 , 则下列选项正确的是( )A、 B、 C、 D、以上选项均不正确2. 设实数满足 , 则函数的最大值是( )A、 B、 C、 D、3. 若角的终边过点 , 则下列选项正确的是( )A、 B、 C、 D、4. 函数f(x)= 在[- , ]。的图像大致为( )A、
 B、
B、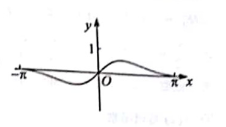 C、
C、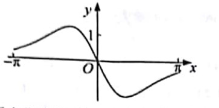 D、
D、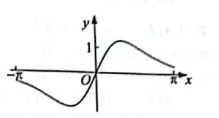 5. “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒。该故事的大意是:齐王有上、中、下三匹马A1,B1,C1,田忌也有上中下三匹马A2, B2, C2, 且这六匹马在比赛中的胜负可用不等式表示如下:A1>A2>B1>B2>C1>C2(注:A>B表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,获得了整场比赛的胜利,创造了以弱胜强的经典案例.已知我方三个数为 , , , 对方的三个数以及排序如表所示:
5. “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒。该故事的大意是:齐王有上、中、下三匹马A1,B1,C1,田忌也有上中下三匹马A2, B2, C2, 且这六匹马在比赛中的胜负可用不等式表示如下:A1>A2>B1>B2>C1>C2(注:A>B表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,获得了整场比赛的胜利,创造了以弱胜强的经典案例.已知我方三个数为 , , , 对方的三个数以及排序如表所示:第一局
第二局
第三局
对方
当时,我方必胜的排序是( )
A、 B、 C、 D、6. 2021年12月,考古工作者又公布了关于北京建城的一件重要文字证据。这次在琉璃河遗址新发现的铭文,不仅是A国建城最早的文字证据,更是北京建城最早的文字证据.考古学家对现场文物样本进行碳14年代学检测,检验出碳14的残留量约为初始量的69%.已知被测物中碳14的质量M随时间t(单位:年)的衰变规律满足(表示碳14原有的质量),据此推测该遗址属于以下哪个时期(参考数据:)( ) A、西周 B、两汉 C、唐朝 D、元朝7. 设函数 , 若关于的方程有四个实根 , , 则的最小值是( )A、15 B、15.5 C、16 D、178. 下列选项正确的是( )A、 B、 C、 D、
A、西周 B、两汉 C、唐朝 D、元朝7. 设函数 , 若关于的方程有四个实根 , , 则的最小值是( )A、15 B、15.5 C、16 D、178. 下列选项正确的是( )A、 B、 C、 D、二、多选题
-
9. 已知 , 则下列等式恒成立的是( )A、 B、 C、 D、10. 对 , 成立的充分不必要条件可以是( )A、 B、 C、 D、11. 王维,字摩诘,号摩诘居士,唐代山水田园派诗人、画家。北宋苏轼在《书摩诘蓝田烟雨图》中评价道:“味摩诘之诗,诗中有画;观摩诘之画,画中有诗。”在王维所做的五言绝句《相思》中,以下诗句不可以作为命题的是( )A、红豆生南国 B、春来发几枝 C、愿君多采撷 D、此物最相思12. 已知函数是定义域为的奇函数,满足 , 且当时, , 则( )A、 B、不等式的解集是 C、函数是周期函数 D、当关于的方程恰有两个不同的解时,
三、填空题
-
13. 函数的定义域为 .14. 已知 , 则的值为 .15. 已知函数的最小正周期是π,且的图象过点 , 则的图象的对称中心坐标为.16. 已知 , 若对恒成立,则实数.
四、解答题
-
17. 设集合 , , .(1)、 , 求;(2)、若“”是“”的充分条件,求的取值范围.18. 已知函数.(1)、判断函数的奇偶性并证明;(2)、判断函数在区间上的单调性,并用单调性的定义证明你的结论.19. 已知函数 .(1)、求的最小正周期;(2)、将的图象上的各点_________得到的图象,当时,方程有解,求实数m的取值范围.
在以下①、②中选择一个,补在(2)中的横线上,并加以解答,如果①、②都做,则按①给分.
①向左平移个单位,再保持纵坐标不变,横坐标缩短到原来的一半.
②纵坐标保持不变,横坐标伸长到原来的2倍,再向右平移个单位.
20. 北京冬奥会已于月日开幕,“冬奥热”在国民中迅速升温,与冬奥会相关的周边产品也销量上涨.因可爱而闻名的冰墩墩更是成为世界顶流,在国内外深受大家追捧.对某商户所售的冰墩墩在过去的一个月内(以天计)的销售情况进行调查发现:冰墩墩的日销售单价(元/套)与时间(被调查的一个月内的第天)的函数关系近似满足(常数),冰墩墩的日销量(套)与时间的部分数据如表所示:(套)
已知第天该商品日销售收入为元,现有以下三种函数模型供选择:
① , ② , ③
(1)、选出你认为最合适的一种函数模型,来描述销售量与时间的关系,并说明理由;(2)、根据你选择的模型,预估该商品的日销售收入( , )在哪天达到最低.
