第27章 圆 章末提升综合测试 华师大版九年级下册同步练习
试卷更新日期:2023-01-07 类型:单元试卷
一、单选题
-
1. 如图,是的直径,为弦, , 在上任取一点D,且点D与点C位于直径的两侧,连接和 , 则的度数是( )
 A、 B、 C、 D、2. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( )
A、 B、 C、 D、2. 一块圆形宣传标志牌如图所示,点A,B,C在⊙O上,CD垂直平分AB于点D.现测得AB=8dm,DC=2dm,则圆形标志牌的半径为( ) A、6dm B、5dm C、4dm D、3dm3. 如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、BC,已知⊙O的半径为2,AB=2,则∠BCD的大小为( )
A、6dm B、5dm C、4dm D、3dm3. 如图,在⊙O中,直径CD垂直弦AB于点E,连接OB、BC,已知⊙O的半径为2,AB=2,则∠BCD的大小为( ) A、20° B、30° C、15° D、25°4. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE与BCFG,点M,N,P,Q分别是DE,FG,弧AC,弧BC的中点.若MP+NQ=14,AC+BC=18,则AB的长是( )
A、20° B、30° C、15° D、25°4. 如图,C是以AB为直径的半圆O上一点,连结AC,BC,分别以AC,BC为边向外作正方形ACDE与BCFG,点M,N,P,Q分别是DE,FG,弧AC,弧BC的中点.若MP+NQ=14,AC+BC=18,则AB的长是( ) A、 B、 C、13 D、165. 如图,水平放置的圆柱形排水管的截面为 , 有水部分弓形的高为2,弦.则截面的半径为( )
A、 B、 C、13 D、165. 如图,水平放置的圆柱形排水管的截面为 , 有水部分弓形的高为2,弦.则截面的半径为( ) A、 B、4 C、 D、86. 如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为( )
A、 B、4 C、 D、86. 如图,四边形ABCD为矩形,AB=3,BC=4,点P是线段BC上一动点,点M为线段AP上一点,∠ADM=∠BAP,则BM的最小值为( ) A、 B、 C、- D、-27. 如图,的两条弦 , 互相垂直,垂足为 , 直径交线段于点 , 且 , 点是的中点.下列结论正确的个数是( )
A、 B、 C、- D、-27. 如图,的两条弦 , 互相垂直,垂足为 , 直径交线段于点 , 且 , 点是的中点.下列结论正确的个数是( )①;②;③是等腰三角形;④ .
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
8. 一个扇形的面积为2πcm2 , 半径为4cm,则这个扇形的圆心角为.9. 如图,AB是⊙O的直径,D,C是弧BE的三等分点,∠COD=32°,则∠E的度数是 .
 10. 如图,是的直径,弦垂足为若 , 则的半径为.
10. 如图,是的直径,弦垂足为若 , 则的半径为.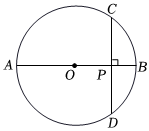 11. 如图,⊙O中,弦AC= , 沿AC折叠劣弧交直径AB于D,DB= , 则直径AB= .
11. 如图,⊙O中,弦AC= , 沿AC折叠劣弧交直径AB于D,DB= , 则直径AB= . 12. “一切为了U”是常山在赶考共同富裕道路上,最新确定的城市品牌.已知线段 , 对于坐标平面内的一个动点P,如果满足 , 则称点P为线段的“U点”,如图,二次函数与x轴交于点A和点B.(1)线段的长度为;(2)若线段的“U”点落在y轴的正半轴上,则该“U点”的坐标为 .
12. “一切为了U”是常山在赶考共同富裕道路上,最新确定的城市品牌.已知线段 , 对于坐标平面内的一个动点P,如果满足 , 则称点P为线段的“U点”,如图,二次函数与x轴交于点A和点B.(1)线段的长度为;(2)若线段的“U”点落在y轴的正半轴上,则该“U点”的坐标为 . 13. 如图,⊙P与x轴交于点A(-5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为.
13. 如图,⊙P与x轴交于点A(-5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为.
三、作图题
-
14. 如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,的三个顶点 , , 均在格点上.
 (1)、画出向左平移5个单位后的图形 , 并写出点的坐标.(2)、画出绕顺时针旋转后的图形 , 并写出点的坐标.(3)、在(2)的条件下,求到所经过的路径长.
(1)、画出向左平移5个单位后的图形 , 并写出点的坐标.(2)、画出绕顺时针旋转后的图形 , 并写出点的坐标.(3)、在(2)的条件下,求到所经过的路径长.四、解答题
-
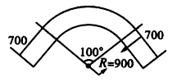
15. 弯制管道时,先按中心计算“展直长度”再下料,试计算图中所示管道的展直长度。(π≈3.14,单位:cm,精确到1cm,弯制管道的粗细不计)
 16. 已知AB为 的直径,EF切 于点D , 过点B作 于点H交 于点C , 连接BD .
16. 已知AB为 的直径,EF切 于点D , 过点B作 于点H交 于点C , 连接BD .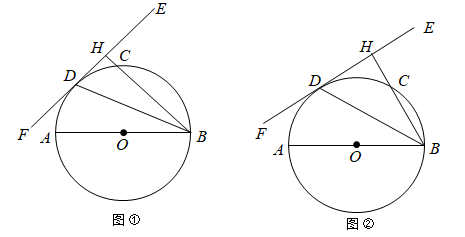 (1)、如图①,若 ,求 的大小;(2)、如图②,若C为弧BD的中点,求 的大小.17. 如图,在 中,直径 与弦 相交于点 , .
(1)、如图①,若 ,求 的大小;(2)、如图②,若C为弧BD的中点,求 的大小.17. 如图,在 中,直径 与弦 相交于点 , .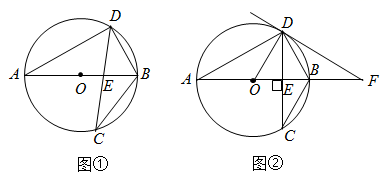
(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若 ,过点 作 的切线 ,与 的延长线相交于点 .求 的大小.
五、综合题
-
18. 如图1,是的直径,且 , 过点作的垂线,C是垂线上一点,连接交于点D,连接 , 点E是的中点,连接交于点F.
 (1)、求证:;(2)、若 , 求的值;(3)、若图1的基础上,作的平分线交于点I,交于点G,连接(如图2),直接写出的最小值.19. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.
(1)、求证:;(2)、若 , 求的值;(3)、若图1的基础上,作的平分线交于点I,交于点G,连接(如图2),直接写出的最小值.19. 在数学兴趣小组活动中,同学们对菱形的折叠问题进行了探究.如图(1),在菱形中,为锐角,为中点,连接 , 将菱形沿折叠,得到四边形 , 点的对应点为点 , 点的对应点为点.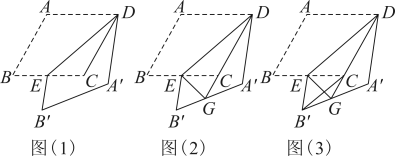 (1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.20. 已知:的两条弦 , 相交于点M,且.
(1)、【观察发现】与的位置关系是;(2)、【思考表达】连接 , 判断与是否相等,并说明理由;(3)、如图(2),延长交于点 , 连接 , 请探究的度数,并说明理由;(4)、【综合运用】如图(3),当时,连接 , 延长交于点 , 连接 , 请写出、、之间的数量关系,并说明理由.20. 已知:的两条弦 , 相交于点M,且. (1)、如图1,连接.求证:.(2)、如图2,若 , 点E为弧上一点, , 交于点F,连接、.
(1)、如图1,连接.求证:.(2)、如图2,若 , 点E为弧上一点, , 交于点F,连接、.①求的度数(用含的代数式表示).
②若 , , 求的面积.
-