27.4 正多边形和圆 华师大版九年级下册同步练习
试卷更新日期:2023-01-07 类型:同步测试
一、单选题
-
1. 如图,五边形是⊙O的内接正五边形,则的度数为( )
 A、 B、 C、 D、2. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )
A、 B、 C、 D、2. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )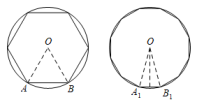 A、 B、 C、 D、3. 如图,的内接正六边形的边心距为 , 分别以、、为圆心,正六边形的半径画弧,则图中阴影部分的面积是( )
A、 B、 C、 D、3. 如图,的内接正六边形的边心距为 , 分别以、、为圆心,正六边形的半径画弧,则图中阴影部分的面积是( )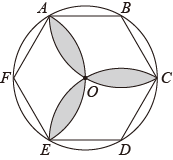 A、 B、 C、 D、4. 如图, , 是 的两条弦,且 ,点 , 分别在 , 上.若 ,则 的度数为( )
A、 B、 C、 D、4. 如图, , 是 的两条弦,且 ,点 , 分别在 , 上.若 ,则 的度数为( ) A、119° B、112° C、109° D、108°5. 如图,面积为18的正方形 内接于 ,则弧 的长度为( )
A、119° B、112° C、109° D、108°5. 如图,面积为18的正方形 内接于 ,则弧 的长度为( ) A、 B、 C、 D、6. 如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( )
A、 B、 C、 D、6. 如图,边AB是⊙O内接正六边形的一边,点C在上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n的值是( ) A、6 B、12 C、24 D、487. ⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )A、1∶ B、 ∶ C、3∶2 D、1∶28. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、6 B、12 C、24 D、487. ⊙O内有一个内接正三角形和一个内接正方形,则内接三角形与内接正方形的边长之比为( )A、1∶ B、 ∶ C、3∶2 D、1∶28. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )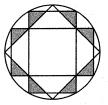 A、1 B、 C、 D、
A、1 B、 C、 D、二、填空题
-
9. 如图,正六边形和正五边形内接于 , 且有公共顶点A,则的度数为度.
 10. 已知圆的周长是 , 则该圆的内接正三角形的边心距是 .11. 如图,如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边,BC一定是圆O的内接正n边形的一条边,那么n= .
10. 已知圆的周长是 , 则该圆的内接正三角形的边心距是 .11. 如图,如果AB、AC分别是圆O的内接正三角形和内接正方形的一条边,BC一定是圆O的内接正n边形的一条边,那么n= . 12. 如图,边长为2的正方形ABCD内接于⊙O,则的长为.(结果保留π)
12. 如图,边长为2的正方形ABCD内接于⊙O,则的长为.(结果保留π) 13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
13. 我国魏晋时期的数学家刘徽首创“割圆术”,利用圆的内接正多边形来确定圆周率.若设⊙O的半径为R , 圆内接正n边形的边长、面积分别为an , Sn , 圆内接正2n边形边长、面积分别为a2n , S2n . 刘徽用以下公式求出a2n和S2n . , .如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 . 14. 如图,边长为2的正方形ABCD内接于⊙O,点E是上一点(不与A、B重合),点F是上一点,连接OE,OF,分别与AB,BC交于点G,B,且∠EOF=90°.有下列结论:①=;②四边形OGBH的面积随着点E位置的变化而变化;③△GBH周长的最小值为2+;④若BG=1﹣ , 则BG,GE,围成的面积是 , 其中正确的是 . (把所有正确结论的序号都填上)
14. 如图,边长为2的正方形ABCD内接于⊙O,点E是上一点(不与A、B重合),点F是上一点,连接OE,OF,分别与AB,BC交于点G,B,且∠EOF=90°.有下列结论:①=;②四边形OGBH的面积随着点E位置的变化而变化;③△GBH周长的最小值为2+;④若BG=1﹣ , 则BG,GE,围成的面积是 , 其中正确的是 . (把所有正确结论的序号都填上)
三、解答题
-
15. 已知圆内接正十二边形的面积为S,求同圆的内接正六边形的面积.
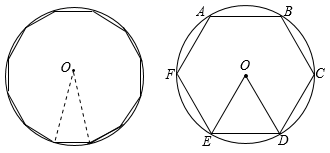 16. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),求 的余角的度数.
16. 如图,正五边形 内接于 , 为 上的一点(点 不与点 重合),求 的余角的度数.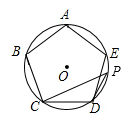 17. 如图, 是 的内接正五边形.求证: .
17. 如图, 是 的内接正五边形.求证: .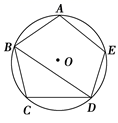
四、综合题
-
18. 阅读下列材料,并按要求完成相应的任务.
黄金三角形与五角星
当等腰三角形的顶角为36°(或108°)时,它的底与腰的比(或腰与底的比)为 , 我们把这样的三角形叫做黄金三角形.
按下面的步骤画一个五角星(如图):
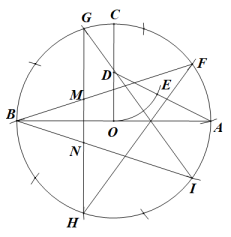
①作一个以AB为直径的圆,圆心为O;
②过圆心O作半径OC⊥AB;
③取OC的中点D,连接AD;
④以D为圆心OD为半径画弧交AD于点E;
⑤从点A开始以AE为半径顺时针依次画弧,
正好把⊙O十等分(其中点F,G,B,H,I为五等分点);
⑥以点F,G,B,H,I为顶点画出五角星.
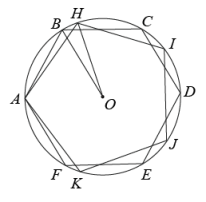
任务:
(1)、求出的值为;(2)、如图,GH与BF,BI分别交于点M,N,求证:△BMN是黄金三角形.19. 已知某种月饼形状的俯视图如图1所示,该形状由1个正六边形和6个半圆组成,半圆直径与正六边形的边长相等.
现商家设计了2种棱柱体包装盒,其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率= ×100%)
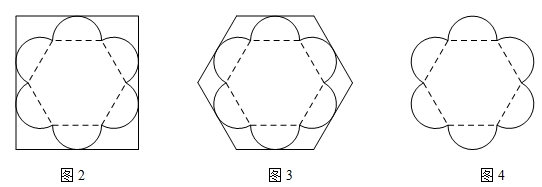 (1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.
(1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%);(2)、考虑到节约成本,商家希望底面利用率能够不低于80%,且底面图形仍然采用最基本的几何形状,请问商家的要求是否能够满足,若可以满足,请设计一种方案,并直接写出此时的利用率;若不能满足,请说明理由.