27.1 圆的认识 华师大版九年级下册同步练习
试卷更新日期:2023-01-07 类型:同步测试
一、单选题
-
1. 下列说法中,正确的是( )A、长度相等的弧是等弧 B、圆的每一条直径都是它的对称轴 C、直径如果平分弦就一定垂直弦 D、直径所对的弧是半圆2. 如图,的直径垂直弦于点E,且 , , 则的长为( ).
 A、2 B、3 C、 D、3. 下列命题正确的是( )A、长度相等的弧是等弧 B、平分弦的直径垂直于弦,并且平分弦所对的弧 C、不在同一直线上的三点确定一个圆 D、圆内接三角形一定是等边三角形4. 如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( )
A、2 B、3 C、 D、3. 下列命题正确的是( )A、长度相等的弧是等弧 B、平分弦的直径垂直于弦,并且平分弦所对的弧 C、不在同一直线上的三点确定一个圆 D、圆内接三角形一定是等边三角形4. 如图,点D是直径为10的中一点,若长为3,则过点D的所有弦中,最长弦与最短弦的长度差为( ) A、2 B、6 C、14 D、185. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径
A、2 B、6 C、14 D、185. 高速公路的隧道和桥梁最多.如图是一个隧道的横截面,若它的形状是以为圆心的圆的一部分,路面米,净高米,则此圆的半径 A、6米 B、米 C、7米 D、米6. 如图,是的直径,点E在上,点D,C是的三等分点, , 则的度数是( )
A、6米 B、米 C、7米 D、米6. 如图,是的直径,点E在上,点D,C是的三等分点, , 则的度数是( ) A、 B、 C、 D、7. 如图,已知的半径为1,则它的内接正方形的边长为( )
A、 B、 C、 D、7. 如图,已知的半径为1,则它的内接正方形的边长为( )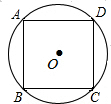 A、 B、2 C、1 D、8. 如图,为的直径,点为圆上一点,将劣弧沿弦翻折交于点 , 连结 , 点与圆心不重合, , 则的度数为( )
A、 B、2 C、1 D、8. 如图,为的直径,点为圆上一点,将劣弧沿弦翻折交于点 , 连结 , 点与圆心不重合, , 则的度数为( ) A、 B、 C、 D、9. 我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1::2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( )
A、 B、 C、 D、9. 我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1::2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( ) A、①② B、①③ C、②④ D、③④
A、①② B、①③ C、②④ D、③④二、填空题
-
10. 如图,是的直径,是的弦, , , 垂足为M, , 则半径的长为
 11. 如图,已知是的直径,过点D的弦平行于半径 , 若的度数是 , 求的度数.
11. 如图,已知是的直径,过点D的弦平行于半径 , 若的度数是 , 求的度数. 12. ⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB与CD的距离为.13. 在⊙O中,点C,D在⊙O上,且分布在直径AB异侧,延长CO交弦BD于点E,若∠DEC=120°,且点A为中点,则的度数为 .
12. ⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB与CD的距离为.13. 在⊙O中,点C,D在⊙O上,且分布在直径AB异侧,延长CO交弦BD于点E,若∠DEC=120°,且点A为中点,则的度数为 . 14. 如图,在Rt△ABC中,∠ACB=90°,AC<BC,CD平分∠ACB交AB于点D,以DB为直径作⊙O,分别交CD,BC于点E,F,连结BE,EF.则∠EBF=度;若DE=DC, BC=8,则EF的长为
14. 如图,在Rt△ABC中,∠ACB=90°,AC<BC,CD平分∠ACB交AB于点D,以DB为直径作⊙O,分别交CD,BC于点E,F,连结BE,EF.则∠EBF=度;若DE=DC, BC=8,则EF的长为
三、解答题


