27.1.3 圆周角 华师大版九年级下册同步练习
试卷更新日期:2023-01-07 类型:同步测试
一、单选题
-
1. 将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.若点A、B的读数分别为86°,30°,则∠ACB的度数是( )
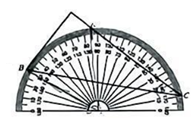 A、28° B、30° C、36° D、56°2. 如图,已知是的外接圆,是的直径,是的弦, , 则等于( )
A、28° B、30° C、36° D、56°2. 如图,已知是的外接圆,是的直径,是的弦, , 则等于( )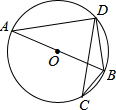 A、 B、 C、 D、3. 如图,点A,B,C在⊙O上, , 则的度数为( )
A、 B、 C、 D、3. 如图,点A,B,C在⊙O上, , 则的度数为( ) A、 B、 C、 D、4. 如图,点、、是上的点, , 连结交于点 , 若 , 则的度数为( )
A、 B、 C、 D、4. 如图,点、、是上的点, , 连结交于点 , 若 , 则的度数为( ) A、 B、 C、 D、5. 如图所示,△ABC的三个顶点在⊙O上,D是上的点,E是上的点,若∠BAC=50°.则∠D+∠E=( )
A、 B、 C、 D、5. 如图所示,△ABC的三个顶点在⊙O上,D是上的点,E是上的点,若∠BAC=50°.则∠D+∠E=( ) A、220° B、230° C、240° D、250°6. 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( )
A、220° B、230° C、240° D、250°6. 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=75°,则∠OAC的大小是( ) A、25° B、50° C、65° D、75°7. AB是⊙O的直径,点C在圆上,∠ABC=65°,那么∠OCA的度数是( )
A、25° B、50° C、65° D、75°7. AB是⊙O的直径,点C在圆上,∠ABC=65°,那么∠OCA的度数是( ) A、25° B、35° C、15° D、20°8. 如图1,是清代数学家李之铉在他的著作《几何易简集》中研究过的一个图形,小圆同学在研究该图形后设计了图2,延长正方形的边至点 , 作矩形 , 以为直径作半圆交于点 , 以为边做正方形 , 在上,记正方形 , 正方形 , 矩形的面积分别为 , , , 则( )
A、25° B、35° C、15° D、20°8. 如图1,是清代数学家李之铉在他的著作《几何易简集》中研究过的一个图形,小圆同学在研究该图形后设计了图2,延长正方形的边至点 , 作矩形 , 以为直径作半圆交于点 , 以为边做正方形 , 在上,记正方形 , 正方形 , 矩形的面积分别为 , , , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,C、D两点在以AB为直径的圆上,AB=2,∠ACD=30°,则AD=.
 10. 如图,内接于 , , D是的中点,且 , 分别是边上的高,则的大小度.
10. 如图,内接于 , , D是的中点,且 , 分别是边上的高,则的大小度. 11. 如图,四边形ABCD是⊙O的内接正方形,E是的中点,AE交BC于点F,则∠1=度.
11. 如图,四边形ABCD是⊙O的内接正方形,E是的中点,AE交BC于点F,则∠1=度. 12. 如图, 在直角坐标系中, 抛物线交轴于点 , 点是点 关于对称轴的对称点, 点是抛物线的顶点, 若的外接圆经过原点 , 则点的坐标为.
12. 如图, 在直角坐标系中, 抛物线交轴于点 , 点是点 关于对称轴的对称点, 点是抛物线的顶点, 若的外接圆经过原点 , 则点的坐标为.
三、解答题

