26.3 实践与探索华师大版九年级下册同步练习

试卷更新日期：2023-01-07 类型：同步测试

进入出卷网下载

一、单选题

1. 二次函数 $y = x^{2} - 2 x + 3$ 的图象与坐标轴的交点个数有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2. 二次函数y＝x²﹣x﹣2的图形与y轴的交点坐标为（）

A、（﹣1，0） B、（2，0） C、（0，﹣2） D、（0，2）

查看试题解析
3. 如图，抛物线y₁＝ax²+bx+c与直线y₂＝mx+n相交于点（3，0）和（0，3），若ax²+bx+c＞mx+n，则x的取值范围是（）

A、0＜x＜3 B、1＜x＜3 C、x＜0或x＞3 D、x＜1减x＞3

查看试题解析
4. 将进货单价为30元的某种商品按零售价100元1件卖出时，每天能卖出20件．若这种商品的零售价在一定范围内每降价1元，其日销售量就增加1件，为了获得最大的利润，则应降价（）

A、5元 B、15元 C、25元 D、35元

查看试题解析
5. 已知抛物线y＝x²+bx+c的部分图象如图所示，若y＜0，则x的取值范围是（）

A、-1＜x＜4 B、-1＜x＜3 C、x＜-1或x＞4 D、x＜-1或x＞3

查看试题解析
6. 已知抛物线 $y = (x - 3)^{2} + c$ 经过点 $A (2 ， 0)$ ，则该抛物线与 $x$ 轴的另一个交点是（）

A、 $(3 ， 0)$ B、 $(4 ， 0)$ C、 $(- 8 ， 0)$ D、 $(- 4 ， 0)$

查看试题解析
7. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象关于直线 $x = 1$ 对称，与x轴交于 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ 两点，若 $- 2 < x_{1} < - 1$ ，则下列四个结论：① $3 < x_{2} < 4$ ， ② $3 a + 2 b > 0$ ， ③ $b^{2} > a + c + 4 a c$ ， ④ $a > c > b$ ．

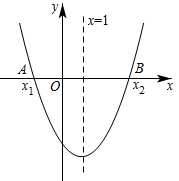
正确结论的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

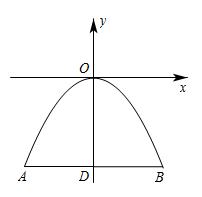
8. 二次函数y＝-2x²+3x+4的图象与y轴的交点坐标是 .

查看试题解析
9. 赵州桥的桥拱横截面是近似的抛物线形，其示意图如图所示，其解析式为y＝- $\frac{1}{25}$ x² ．当水面离桥拱顶的高度DO为4m时，水面宽度AB为m．

查看试题解析
10. 某商场经营一种文具，进价为20元/件，当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件.那么该文具定价为元时每天的最大销售利润最大.

查看试题解析
11. 如图，已知抛物线 $y = a x^{2} + c$ 与直线 $y = k x + m$ 交于 $A (- 4 ， y_{1}) ， B (1 ， y_{2})$ 两点，则关于x的不等式 $a x^{2} + c \geq k x + m$ 的解集是.

查看试题解析
12. 抛物线 $y = x^{2} - 2 x - 3$ 的图象为 $G_{1}$ ， $G_{1}$ 关于 $x$ 轴对称的图象为 $G_{2}$ ， $G_{1}$ 和 $G_{2}$ 组成的图象与直线 $y = x + m$ 有3个公共点时， $m$ 的范围（或值）是．

查看试题解析
13. 已知二次函数y＝﹣x²+4x+5及一次函数y＝﹣x+b，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线y＝﹣x+b与新图象有4个交点时，b的取值范围是．

查看试题解析

三、解答题

14. 在平面直角坐标系中，求抛物线 $y = x^{2} - 2 x - 1$ 与x轴的交点坐标．

查看试题解析
15. 已知抛物线 $y = x^{2} + (2 m + 1) x + m^{2}$ 与x轴有交点，求m的取值范围．

查看试题解析
16. 某商场购进一批单价为40元的商品，若按每件50元销售，平均每天可销售90件．市场调查发现，这种商品的销售单价每提高1元，平均每天少销售3件．将销售单价定为多少，才能使每天所获销售利润W最大？最大利润W是多少？

查看试题解析

四、综合题

17. k为任意实数，已知二次函数 $y = x^{2} - 2 k x - k$ 的图象与x轴有两个不同的交点 $A (x_{1} ， 0)$ ， $B (x_{2} ， 0)$ ．

(1)、填空： $x_{1} + x_{2} =$ ；（用含k的代数式表示）

(2)、若 $k = 2$ ，求 $2 k x_{1} + x_{2}^{2}$ 的值；

(3)、求证： $2 k x_{1} + x_{2}^{2} + 3 k > 0$ ．

查看试题解析
18. 阅读材料：一般地，对于某个函数，如果自变量x在取值范围内任取x＝a与x＝ $- a$ 时，函数值相等，那么这个函数是“对称函数”.例如，y＝x² ，在实数范围内任取x＝a时，y＝a²；当x＝ $- a$ 时，y＝ ${(- a)}^{2}$ ＝ a² ，所以y＝x²是“对称函数”.

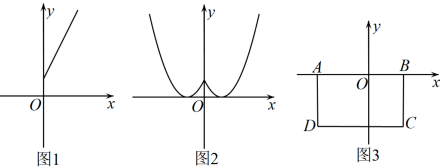(1)、函数 $y = 2 | x | + 1$ 对称函数（填“是”或“不是”）.当x≥0时， $y = 2 | x | + 1$ 的图象如图1所示，请在图1中画出x＜0时， $y = 2 | x | + 1$ 的图象.

(2)、函数 $y = x^{2} - 2 | x | + 1$ 的图象如图2所示，当它与直线y＝－x+n恰有3个交点时，求n的值.

(3)、如图3，在平面直角坐标系中，矩形ABCD的顶点坐标分别是A（－3，0），B（2，0），C（2，－3），D（－3，－3），当二次函数 $y = x^{2} - b | x | + 1$ （b>0）的图象与矩形的边恰有4个交点时，求b的取值范围.

查看试题解析

26.3 实践与探索 华师大版九年级下册同步练习

一、单选题

二、填空题

三、解答题

四、综合题

26.3 实践与探索华师大版九年级下册同步练习