26.2.2 二次函数y=ax2+bx+c的图像与性质华师大版九年级下册同步练习

试卷更新日期：2023-01-07 类型：同步测试

进入出卷网下载

一、单选题

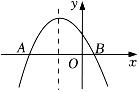
1. 把抛物线 $y = - x^{2}$ 向右平移1个单位，再向下平移2个单位，所得抛物线是（）

A、 $y = (x - 1)^{2} + 2$ B、 $y = - (x - 1)^{2} + 2$ C、 $y = - (x + 1)^{2} + 2$ D、 $y = - (x - 1)^{2} - 2$

查看试题解析
2. 抛物线y＝-2（x+1）²-2的顶点坐标是（）

A、（1，2） B、（1，-2） C、（-1，2） D、（-1，-2）

查看试题解析
3. 已知 $y = - x^{2} + 4 x - 1$ ，当 $1 \leq x \leq 5$ 时，y的最小值是（）

A、2 B、3 C、 $- 8$ D、 $- 6$

查看试题解析
4. 如图，二次函数y＝a（x+1）²+k的图象与x轴交于A（-3，0），B两点，下列说法错误的是（）

A、a＜0 B、当x＜0时，y随x的增大而增大 C、点B的坐标为（1，0） D、图象的对称轴为直线x＝-1

查看试题解析
5. 若二次函数 $y = x^{2} + b x + 5$ 配方后为 $y = (x - 3)^{2} - 4$ ，则 $b$ 的值分别为（）

A、0 B、5 C、6 D、-6

查看试题解析
6. 已知抛物线 $y = a x^{2} - 2$ 与 $x$ 轴所围成的封闭区域内 $($ 含边界 $)$ ，横、纵坐标均为整数的点有且只有7个，则 $a$ 的取值范围为（）

A、 $1 < a < 2$ B、 $1 \leq a < 2$ C、 $\frac{1}{2} < a < 1$ D、 $\frac{1}{2} < a \leq 1$

查看试题解析
7. 已知二次函数y=（x-m+2）（x+m-4）+n，其中m，n为常数，则（）

A、m>1，n<0时，二次函数的最小值大于0 B、m=1，n>0时，二次函数的最小值大于0 C、m<1，n>0时，二次函数的最小值小于0 D、m=1，n<0时，二次函数的最小值小于0

查看试题解析
8. 如图，二次函数y＝ax²+bx+c的图象与y轴正半轴相交，其顶点坐标为（ $\frac{1}{2}$ ， 1），下列结论：①abc＜0；②a+b＝0；③4ac-b²＝4a；④a+b+c＜0．其中正确的有（）个．

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 将抛物线 $y = x^{2} + 1$ 向右平移2个单位长度后所得的抛物线的函数表达式为.

查看试题解析
10. 若 $A (\frac{3}{4} ， y_{1})$ ， $B (- \frac{5}{4} ， y_{2})$ ， $C (\frac{1}{4} ， y_{3})$ 为二次函数 $y = x^{2} + 4 x - 5$ 的图象上的三点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是．（用“ $<$ ”连接）

查看试题解析
11. 抛物线 $y = - x^{2} + 3 x - \frac{5}{2}$ 的对称轴是直线．

查看试题解析
12. 已知，点A（1，m）和点B（3，n）在二次函数y＝ax²+bx+1（a≠0）的图象上，若点C（x₀ ， y₀）是该二次函数图象上任意一点，且满足y₀≥m，mn的最大值为 .

查看试题解析
13. 小明在学习“二次函数”内容后，进行了反思总结．如图，二次函数y＝ax²+bx+c（a≠0）图像的一部分与x轴的一个交点坐标为（1，0），对称轴为直线x＝﹣1，结合图像他得出下列结论：①ab＞0且c＞0；②a+b+c＝0；③关于x的一元二次方程ax²+bx+c＝0（a≠0）的两根分别为﹣3和1；④若点（﹣4，y₁），（﹣2，y₂），（3，y₃）均在二次函数图象上，则y₁＜y₂＜y₃；⑤3a+c＜0，其中正确的结论有．（填序号，多选、少选、错选都不得分）

查看试题解析

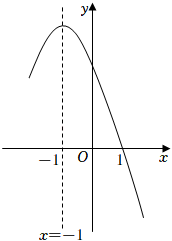
三、解答题

14. 已知抛物线 $y = 2 x^{2} - 6 x + 3$ ．请用配方法将其化为 $y = a {(x - h)}^{2} + k$ 的形式，并写出其开口方向、对称轴及顶点坐标．

查看试题解析
15. 已知二次函数 $y = a x^{2} + b x - 3$ ．若函数图象经过点（1，-4），（-1，0），求 $a$ ， $b$ 的值．

查看试题解析
16. 已知 $y$ 是关于 $x$ 的二次函数 $y = - \frac{1}{2} {(x - 2 m)}^{2} + 3 - m$ （ $m$ 是实数）．小明说该二次函数图象的顶点在直线 $y = - \frac{1}{2} x + 3$ 上，你认为他的说法对吗？为什么？

查看试题解析

四、综合题

17. 综合与探究
已知二次函数 $y = a x^{2} - 2 a x + b$ ．

(1)、其图象的对称轴为直线．

(2)、若 $a > 0$ ，且该二次函数的图象经过点 $(- 2 ， c) ， (1 ， d) ， (2 ， e) ， (3 ， f)$ ，试比较c，d，e，f的大小，并说明理由．

(3)、若该二次函数的图象经过点 $(0 ， 2)$ ，且抛物线与x轴所围成的封闭图形内有4个整数点（不包括边界），求出a的取值范围．（注：横纵坐标均为整数的点为整数点）

查看试题解析
18. 如图，已知抛物线 $y = - x^{2} + b x + c$ 与坐标轴交于 $A$ ， $B$ ， $C$ 三点，其中 $A (- 2 ， 0)$ ， $B (4 ， 0)$ .

(1)、求该抛物线的表达式；

(2)、根据图象，直接写出 $y > 0$ 时， $x$ 的取值范围；

(3)、若要使抛物线与 $x$ 轴只有一个交点，则需将抛物线向下平移几个单位？

查看试题解析

26.2.2 二次函数y=ax2+bx+c的图像与性质 华师大版九年级下册同步练习

一、单选题

二、填空题

三、解答题

四、综合题

26.2.2 二次函数y=ax2+bx+c的图像与性质华师大版九年级下册同步练习