陕西省韩城市新城四中2022-2023学年九年级上学期期末调研试卷数学
试卷更新日期:2023-01-07 类型:期末考试
一、选择题(共8小题,每小题3分,计24分.)
-
1. “购买1张彩票,恰好中奖”这个事件是( )A、必然事件 B、随机事件 C、确定事件 D、不可能事件2. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 用配方法解一元二次方程 , 此方程可变形为( )A、 B、 C、 D、4. 如图,在中, , , 则的度数是( )
3. 用配方法解一元二次方程 , 此方程可变形为( )A、 B、 C、 D、4. 如图,在中, , , 则的度数是( ) A、80° B、70° C、60° D、50°5. 一个不透明的袋子中放入三个除标号外其余均相同的小球,三个小球的标号分别是2,1,-1,随机从这个袋子中一次取出两个小球,取出的两个小球上数BK字之积为负数的概率是( )A、 B、 C、 D、6. 已知关于的一元二次方程有两个实数根 , , 若 , 则的值为( )A、1 B、-1 C、2 D、-27. 某公园中央地上有一个大理石球,小明想测量球的半径,于是找了两块厚20cm的砖塞在球的两侧(其中间的截面图如图所示),他量了下两砖之间的距离刚好是80cm,则图中截面圆的半径是( )
A、80° B、70° C、60° D、50°5. 一个不透明的袋子中放入三个除标号外其余均相同的小球,三个小球的标号分别是2,1,-1,随机从这个袋子中一次取出两个小球,取出的两个小球上数BK字之积为负数的概率是( )A、 B、 C、 D、6. 已知关于的一元二次方程有两个实数根 , , 若 , 则的值为( )A、1 B、-1 C、2 D、-27. 某公园中央地上有一个大理石球,小明想测量球的半径,于是找了两块厚20cm的砖塞在球的两侧(其中间的截面图如图所示),他量了下两砖之间的距离刚好是80cm,则图中截面圆的半径是( ) A、80cm B、70cm C、60cm D、50cm8. 在平面直角坐标系中,已知二次函数的图象与轴相交于点C,将该二次函数图象向右平移m个单位长度后,也经过点C,则m的值为( )A、2 B、4 C、6 D、8
A、80cm B、70cm C、60cm D、50cm8. 在平面直角坐标系中,已知二次函数的图象与轴相交于点C,将该二次函数图象向右平移m个单位长度后,也经过点C,则m的值为( )A、2 B、4 C、6 D、8二、填空题(共5小题,每小题3分,计15分)
-
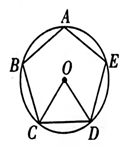
9. 若是关于的一元二次方程的一个根,则的值为.10. 如图,五边形ABCDE是的内接正五边形,则正五边形的中心角的度数为.
 11. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时(指向两个扇形交线处时,重新转动转盘),事件“指针落在蓝色扇形中”的概率为.
11. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时(指向两个扇形交线处时,重新转动转盘),事件“指针落在蓝色扇形中”的概率为. 12. 如图,四边形ABCD内接于 , BC为的直径,.若 , 则的度数为°.
12. 如图,四边形ABCD内接于 , BC为的直径,.若 , 则的度数为°.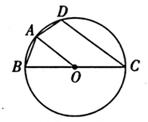 13. 如图,在矩形ABCD中, , , 点E,F,G,H依次是边AB,BC,CD,DA上的点(不与各顶点重合),且 , 记四边形EFGH面积为S(图中阴影),则S的最大值为.
13. 如图,在矩形ABCD中, , , 点E,F,G,H依次是边AB,BC,CD,DA上的点(不与各顶点重合),且 , 记四边形EFGH面积为S(图中阴影),则S的最大值为.
三、解答题(共13小题,计81分.)
-
14. 解方程:.15. 如图,在中, , 将绕点C逆时针旋转50°得到 , 且于点D,求的度数.
 16. 已知关于x的方程有两个实数根 , , 求的取值范围.17. 如图,已知 , 利用尺规作图法作的外接圆.(不写作法,保留作图痕迹)
16. 已知关于x的方程有两个实数根 , , 求的取值范围.17. 如图,已知 , 利用尺规作图法作的外接圆.(不写作法,保留作图痕迹) 18. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
18. 如图,在平面直角坐标系中,已知的三个顶点的坐标分别为 , , .
⑴若和关于原点О成中心对称图形,作出 , 点A、B、C的对应点分别为点、、;
⑵将绕着点О按顺时针方向旋转90°得到 , 作出 , 点A、B、C的对应点分别为点、、.
19. 某玩具公司承接了第19届杭州亚运会吉祥物公仔的生产任务,现对一批公仔进行抽检,其结果统计如下,请根据表中数据,回答问题:抽取的公仔数
10
100
1000
2000
3000
5000
优等品的频数
9
96
951
1900
2856
4750
优等品的频率
0.9
0.96
0.951
0.95
0.952
0.95
(1)、从这批公仔中任意抽取1只公仔是优等品的概率的估计值是;(精确到0.01)(2)、若该公司这一批次生产了10000只公仔,求这批公仔中优等品大约有多少只?20. 如图,扇形AOB的圆心角为90°, , 求阴影部分的面积(结果保留) 21. 某校在践行“安全在我心中,你我一起行动”主题手抄报评比活动中,共设置了“交通安全,消防安全、饮食安全,防疫安全”四个主题内容,推荐亮亮和苗苗两名学生参加评比,若他们每人从以上四个主题内容中随机选择一个,每个主题被选择的可能性相同.
21. 某校在践行“安全在我心中,你我一起行动”主题手抄报评比活动中,共设置了“交通安全,消防安全、饮食安全,防疫安全”四个主题内容,推荐亮亮和苗苗两名学生参加评比,若他们每人从以上四个主题内容中随机选择一个,每个主题被选择的可能性相同. (1)、亮亮选择交通安全手抄报的概率为;(2)、用列表法或画树状图法求亮亮和苗苗选择不同主题手抄报的概率.22. 已知二次函数(其中为常数).(1)、该函数的图象与轴的公共点有个;(2)、若该函数的图象的对称轴是 , 顶点为点A,求此时函数的解析式及点A的坐标.23. 第二十二届中国上海国际艺术节首次移师上海市黄浦区南京东路第一百货商业中心.主办方工作人员准备利用一边靠墙(墙长25米)的空旷场地为提前到场的观众设立面积为320平方米的长方形等候区.如图,为了方便观众进出,在两边空出两个宽各为1米的出人口,共用去隔栏绳50米(靠墙一面不用隔栏绳).请问,工作人员围成的这个长方形的相邻两边长分别是多少米?
(1)、亮亮选择交通安全手抄报的概率为;(2)、用列表法或画树状图法求亮亮和苗苗选择不同主题手抄报的概率.22. 已知二次函数(其中为常数).(1)、该函数的图象与轴的公共点有个;(2)、若该函数的图象的对称轴是 , 顶点为点A,求此时函数的解析式及点A的坐标.23. 第二十二届中国上海国际艺术节首次移师上海市黄浦区南京东路第一百货商业中心.主办方工作人员准备利用一边靠墙(墙长25米)的空旷场地为提前到场的观众设立面积为320平方米的长方形等候区.如图,为了方便观众进出,在两边空出两个宽各为1米的出人口,共用去隔栏绳50米(靠墙一面不用隔栏绳).请问,工作人员围成的这个长方形的相邻两边长分别是多少米? 24. 如图,以的边BC为直径的 , 交AB边于点D,点D为AB的中点,于点E.
24. 如图,以的边BC为直径的 , 交AB边于点D,点D为AB的中点,于点E. (1)、求证:DE是的切线;(2)、若的面积是48, , 求的半径.
(1)、求证:DE是的切线;(2)、若的面积是48, , 求的半径.

