四川省广元市苍溪县2022-2023学年九年级上学期期末数学试卷
试卷更新日期：2023-01-07 类型：期末考试
一、选择题:（本大题共10小题，每小题3分，共30分.）
-
1. 习近平主席在2022年新年贺词中提到“人不负青山，青山定不负人”一语道出“人与自然和谐共生”的至简大道.下列有关环保的四个图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列事件为随机事件的是（ ）A、明天太阳从东方升起 B、从仅装有白球的箱子里取出1个红球 C、掷一次骰子，向上一面的数字是6 D、任意画一个三角形，其内角和为360°3. 如图，四边形ABCD是⊙O的内接四边形，E是BC延长线上一点.若∠BAD＝114°，则∠DCE的度数是（ ）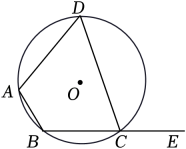
A、124° B、114° C、94° D、66°4. 如图，将△ABC绕点A逆时针旋转65°得到△AED，则∠BAE的度数是（ ）
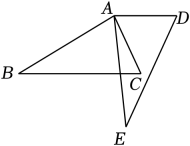A、65° B、45° C、35° D、25°5. 一个不透明的箱子里装有m个球，其中红球3个，这些球除颜色不同其余都相同，每次搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验发现，摸到红球的频率稳定在0.3附近，则可以估算出m的值为（ ）A、3 B、5 C、10 D、126. 如图，点P为⊙O外一点，PA为⊙O的切线，A为切点，PO交⊙O于点B，∠P＝30°，OB＝3，则线段OP的长为（ ）
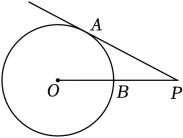A、3 B、 C、6 D、97. 某展览馆计划将长60m，宽40m的矩形场馆重新布置，展览馆的中间是面积为1500m2的一个矩形展览区，四周留有等宽的通道（如图所示），求通道的宽.设通道的宽为xm，根据题意列方程正确的是（ ）
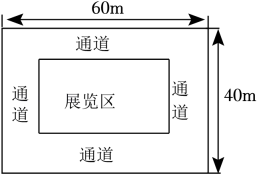A、（60-2x）（40-2x）＝1500 B、（60-2x）（40-x）＝1500 C、（60-x）（40-2x）＝1500 D、（60-x）（40-x）＝15008. 已知关于x的一元二次方程（k-1）x2-4x-1＝0有两个不等的实数根，则k的取值范围是（ ）A、k≥-4 B、k＞-3 C、k＞-3且k≠1 D、k≥-3且k≠19. 如图，二次函数y＝ax2+bx+c的图象经过点A（1，0），B（5，0），下列说法正确的是（ ）
A、c＜0 B、b2-4ac＜0 C、a-b+c＜0 D、图象的对称轴是直线x＝310. 如图，AB是⊙O的弦，AB＝6，C是⊙O上的一个动点，且∠ACB＝45°.若M，N分别是AB，AC的中点，则MN长的最大值是（ ）
A、3 B、6 C、3 D、6二、填空题:（本大题共6小题，每小题4分，共24分.）
-
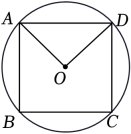
11. 如图，正方形ABCD是⊙O的内接四边形，则∠AOD的度数是.
12. 学校招募运动会广播员，从3名男生和1名女生中随机选取1人，则选中女生的概率是.13. 将抛物线y＝x2先向左平移2个单位长度，再向上平移3个单位长度得到新的抛物线，新抛物线的解析式为.14. 如图所示游戏板中每一个小正方形除颜色外都相同，把游戏板平放到露天地面上，落在该游戏板上的第一滴雨正好打中阴影部分的概率是.
15. 将△OAB按如图的方式放在平面直角坐标系中，其中∠OBA＝90°，∠A＝30°，顶点A的坐标为（1，），将△OAB绕原点O逆时针旋转60°得到点△OA'B′，则点A'的坐标为.
16. 如图，在△ABC中，AB＝AC，∠C＝30°，AC＝4，以AB为直径的⊙O交BC于点D，则图中阴影部分的面积为.
三、解答题：（本大题共10小题，共96分.要求写出必要的解题步骤或证明过程）
-
17. 解下列方程：(1)、x2-4x+2＝0；(2)、2x2+3＝7x.18. 如图，转盘被分成六个相同的扇形，并在上面依次写上数字：2，3，4，5，6，7.指针的位置固定，转动转盘后任其自由停止.
(1)、当转盘停止时，指针指向奇数区域的概率是多少？(2)、当转盘停止时，指针指向的数小于或等于5的概率是多少？19. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB＝20，CD＝16.求AE的长.
20. 为满足师生阅读需求，某校图书馆的藏书量不断增加，2019年年底的藏书量为5万册，2021年年底的藏书量为7.2万册.(1)、求该校这两年藏书的年均增长率；(2)、假设2022年该校藏书的年均增长率与前两年相同，请你预测到2022年年底该校的藏书量是多少？21. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（-3，5），B（-2，1），C（-1，3）.
⑴若△ABC和△A1B1C1关于原点O成中心对称图形，写出△A1B1C1的各点的坐标；
⑵将△ABC绕着点O顺时针方向旋转90°得到△A2B2C2 ， 画出图形并写出△A2B2C2的各点的坐标.
22. 2022卡塔尔世界杯正在激烈进行中，吉祥物“拉伊卜”凭借可爱的造型受到网友喜爱.如图分别是2022年和2018年世界杯的吉祥物和会徽图案，军军制作了4张正面分别印有这四个图案的卡片（卡片的形状、大小、颜色和质地等都相同，这4张卡片分别用字母A，B，C，D表示），并将这4张卡片正面朝下洗匀.
(1)、军军从中随机抽取1张卡片上的图案是吉祥物“拉伊卜”的概率是；(2)、军军从这4张卡片中任意抽取1张卡片，再从剩下的卡片中任意抽取1张卡片，请利用画树状图或列表法，求抽取的2张卡片上的图案都是吉祥物的概率.23. 苍溪独特的土壤、水分、气候组成的生态系统，成为猕猴桃的乐土，被国家誉为“红心猕猴桃第一县、红心猕猴桃之乡”.某水果店销售红心猕猴桃，平均每天可售出120箱，每箱盈利60元，春节临近，为了扩大销售，水果店决定采取适当的降价措施，经调查发现，每箱红心猕猴桃每降价5元，水果店平均每天可多售出20箱.设每箱红心猕猴桃降价x元.(1)、当x＝10时，求销售该红心猕猴桃的总利润；(2)、设每天销售该红心猕猴桃的总利润为w元.①求w与x之间的函数解析式；
②试判断总利润能否达到8200元，如果能达到，求出此时x的值；如果达不到，求出w的最大值.
24. 如图，AB是⊙O的直径，F为⊙O上一点，AC平分∠FAB交⊙O于点C.过点C作CD⊥AF交AF的延长线于点D.
(1)、求证：CD是⊙O的切线.(2)、若DC＝3，AD＝9，求⊙O半径.25. 如图
(1)、如图1，△ACB是等边三角形，点D、E分别在CA、CB上，且CD＝CE.当△DCE绕点C旋转至ΔD1CE1处，使点A、D1、E1在同一直线上（如图2），连接BE1.填空：①∠AE1B的度数为；
②线段AD1、BE1之间的数量关系为.
(2)、如图3，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A、D、E三点在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM、AE、BE之间的数量关系.并说明理由.26. 如图，已知抛物线y＝ax2+bx+3与x轴交于A（-3，0）和B（1，0）两点，与y轴交于点C.
(1)、求抛物线的解析式；(2)、设抛物线的顶点为M，试判断△ACM的形状；(3)、在x轴上方的抛物线上是否存在一点P，使△PAB的面积为8，若存在，直接写出点P的坐标；若不存在，请说明理由.