广西钦州市灵山县2022-2023学年九年级上学期期中数学试卷
试卷更新日期：2023-01-07 类型：期中考试
一、选择题（本大题共12小题，每小题3分，共36分.）
-
1. 下列四个生活安全警示图标，其中是中心对称图形的是（ ）A、
B、
C、
D、
2. 一元二次方程x2-3x＝0的解是（ ）A、x1＝x2＝3 B、x1＝x2＝-3 C、x1＝0，x2＝3 D、x1＝0，x2＝-33. 将抛物线y＝x2先向左平移5个单位，再向下平移4个单位，得到新抛物线的解析式是（ ）A、y＝（x+5）2-4 B、y＝（x+5）2+4 C、y＝（x-5）2-4 D、y＝（x（ ）-5）2+44. 在平面直角坐标系中，点A（3，2）关于原点对称的点的坐标是（ ）A、（-3，2） B、（3，-2） C、（-2，-3） D、（-3，-2）5. 一元二次方程2x2-3x-4＝0根的情况为（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断6. 已知2x2+x-1＝0的两根为x1 ， x2 ， 则x1+x2的值为（ ）A、1 B、-1 C、 D、-7. 已知二次函数y1＝-3x2 ， ， ， 它们的图象开口由小到大的顺序是（ ）A、y1＜y2＜y3 B、y3＜y2＜y1 C、y1＜y3＜y2 D、y2＜y3＜y18. 如图，若被击打的小球飞行高度h（单位：m）与飞行时间t（单位：s）具有函数关系为h＝20t-5t2 ， 则小球从飞出到落地的所用时间为（ ）
A、3s B、4s C、5s D、6s9. 如图，以点A为中心，把△ABC逆时针旋转110°，得到△AB'C′（点B、C的对应点分别为点B′、C′），连接BB'，若AC'∥BB'，则∠CAB'的度数为（ ）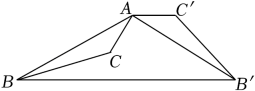
A、45° B、60° C、70° D、75°10. 向阳村2010年的人均收入为12000元，2012年的人均收入为14520元，求人均收入的年平均增长率.设年平均增长率为x，则根据题意可列方程为（ ）A、12000（1-x）2＝14520 B、14520（1-x）2＝12000 C、12000（1+x）2＝14520 D、14520（1+x）2＝1200011. 函数y＝ax＋1与y＝ax2＋bx＋1（a≠0）的图象可能是（ ）A、
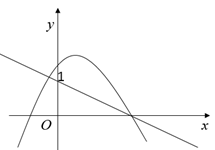B、
C、
D、
12. 如图是抛物线y1＝ax2+bx+c（a≠0）图象的一部分，抛物线的顶点坐标为B（-1，-3），与x轴的一个交点为A（-4，0）.点A和点B均在直线y2＝mx+n（m≠0）上.①2a+b＝0；②abc＜0；③抛物线与x轴的另一个交点是（4，0）；④方程ax2+bx+c＝-3有两个不相等的实数根；⑤a+b+c＞-m+n；⑥不等式mx+n＞ax2+bx+c的解集为-4＜x＜-1.
其中结论正确的是（ ）
A、①④⑥ B、②⑤⑥ C、②③⑤ D、①⑤⑥二、填空题（本大题共6小题，每小题2分，共12分.）
-
13. 抛物线y＝2（x-1）2的对称轴是.14. 如图，以原点为中心，把点A（3，4）逆时针旋转90°，得到点A'，则点A'的坐标是.
15. 两个相邻偶数a，b（a＞0，b＞0）的积是168，这两个偶数的和为.16. 写出一个二次函数，其图象满足：①开口向上；②经过点（0，0），这个二次函数的解析式可以是.17. 如图，将Rt△ABC绕直角顶点顺时针旋转90°，得到△A′B′C，连接AA′，若∠AA′B′＝20°，则∠B的度数为°.
18. 在平面直角坐标系中，抛物线y＝x2的图象如图所示，已知点A的坐标为（1，1），过点A作AA1∥x轴交抛物线于点A1 ， 过点A1作A1A2∥OA交抛物线于点A2 ， 过点A2作A2A3∥x轴交抛物线于点A3 ， 过点A3作A3A4∥OA交抛物线于点A4…，依次进行下去，则点A2022的坐标为.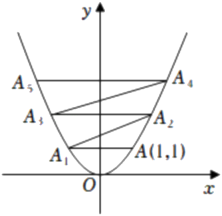
三、解答题（本大题共8题，共72分.）
-
19. 解方程：(1)、x2+4x＝5；(2)、5x2-3x＝x+1.20. 已知m，n是方程x2+x-1＝0的实数根.(1)、求m+n，mn的值；(2)、求m2+2m+n-mn的值.21. 如图，在平面直角坐标系中，△ABC的顶点坐标为A（-2，3），B（-3，2），A（-1，1）.（画图时字母应标注清楚哦）
⑴将△ABC绕原点O顺时针旋转90°，请画出平移后的△A1B1C1；
⑵画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2；
⑶若△A'B'C′与△ABC是中心对称图形，则对称中心的坐标为▲ .
22. 如图，将△ABC绕点A逆时针旋转45°得到△ADE，∠BAC＝45°，AB＝3，AC＝4.
(1)、求∠EAB的度数；(2)、连接BE，求BE的长.23. 如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD（围墙MN最长可利用25m），现在已备足可以砌40m长的墙的材料，
(1)、设计一种砌法，使矩形花园的面积为150m2；(2)、请设计一种砌法，使矩形花园的面积最大.24. 翰林文具连锁超市销售一款钢笔，每支钢笔的成本为20元/支，销售中发现，该钢笔每天的销售量y（支）与销售单价x（元/支）之间存在如图所示的关系.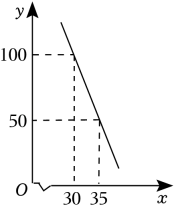
(1)、求y与x之间的函数关系式（不要求写出x的取值范围）；(2)、当销售单价为多少元时，文具超市获利最大？最大利润是多少？25. 在正方形ABCD中，点E在射线BC上（不与点B、C重合），连接DB，DE，将DE绕点E逆时针旋转90°得到EF，连接BF．
(1)、如图1，点E在BC边上．①依题意补全图1；
②若AB＝6，EC＝2，求BF的长；
(2)、如图2，点E在BC边的延长线上，用等式表示线段BD，BE，BF之间的数量关系．26. 如图，抛物线y＝x2+bx+c与x轴交于点A和点B（3，0），与y轴交于点C（0，3）.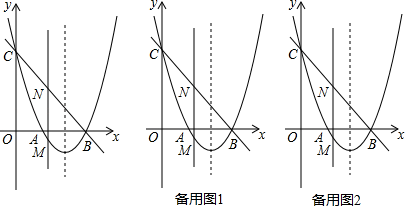
(1)、求抛物线的解析式；(2)、若点M是抛物线在x轴下方上的动点，过点M作MN∥y轴交直线BC于点N，求线段MN的最大值；(3)、在（2）的条件下，当MN取得最大值时，在抛物线的对称轴l上是否存在点P，使△PBN是等腰三角形？若存在，请直接写出所有点P的坐标；若不存在，请说明理由.