广西贺州市平桂区2022-2023学年八年级上学期期末数学试卷
试卷更新日期:2023-01-07 类型:期末考试
一、选择题:(每小题3分,共36分。)
-
1. 点(2,-3)在平面直角坐标系中所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列表达式中,y不是x的函数的是( )A、y=±6x B、y=6x2+x+1 C、y=6x+3 D、y=3. 如下字体的四个汉字中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 在△ABC中,AB=2,BC=3,AC的长不可能的是( )A、1 B、2 C、3 D、45. 在△ABC中,AC=BC,CD为AB边上的高,∠ACB=92°,则∠ACD的度数为( )
4. 在△ABC中,AB=2,BC=3,AC的长不可能的是( )A、1 B、2 C、3 D、45. 在△ABC中,AC=BC,CD为AB边上的高,∠ACB=92°,则∠ACD的度数为( ) A、45° B、46° C、50° D、60°6. 在平面直角坐标系中,将点A(-3,2)向下平移3个单位后得到的点A1的坐标为( )A、(-3,5) B、(-3,3) C、(-3,-1) D、(0,2)7. 函数y=中自变量x的取值范围是( )A、x≥0 B、x>l C、x≥l D、x≠08. 已知等腰三角形ABC的一个角为80°,则该三角形的顶角为( )A、80° B、20° C、80°或20° D、以上都不对9. 已知Rt△ABC≌Rt△EDF,Rt△ABC的面积为12,Rt△EDF的一条直角边等于3,则另一直角边的长是( )A、2 B、4 C、6 D、810. 如图,在平面直角坐标系中,函数y=k(x-1)(k>0)的图象大致是( )A、
A、45° B、46° C、50° D、60°6. 在平面直角坐标系中,将点A(-3,2)向下平移3个单位后得到的点A1的坐标为( )A、(-3,5) B、(-3,3) C、(-3,-1) D、(0,2)7. 函数y=中自变量x的取值范围是( )A、x≥0 B、x>l C、x≥l D、x≠08. 已知等腰三角形ABC的一个角为80°,则该三角形的顶角为( )A、80° B、20° C、80°或20° D、以上都不对9. 已知Rt△ABC≌Rt△EDF,Rt△ABC的面积为12,Rt△EDF的一条直角边等于3,则另一直角边的长是( )A、2 B、4 C、6 D、810. 如图,在平面直角坐标系中,函数y=k(x-1)(k>0)的图象大致是( )A、 B、
B、 C、
C、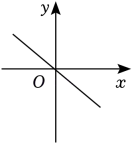 D、
D、 11. 如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点P、Q,作直线PQ交AB于点D,连接AD,若△ABC的周长为15,AB=6,则△ADC的周长为( )
11. 如图,在△ABC中,分别以点A和点B为圆心,大于AB的长为半径画弧,两弧相交于点P、Q,作直线PQ交AB于点D,连接AD,若△ABC的周长为15,AB=6,则△ADC的周长为( )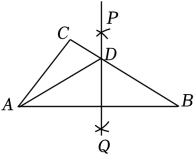 A、6 B、7 C、8 D、912. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )
A、6 B、7 C、8 D、912. 如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )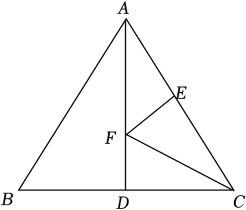 A、30° B、45° C、25° D、20°
A、30° B、45° C、25° D、20°二、填空题:(每小题3分,共18分.)
-
13. 在△ABC中,∠A=40°,∠B=60°,则∠C=°.14. 命题“相等的角是对顶角”是命题(填“真”或“假”)15. 在平面直角坐标系中,与点A(-13,6)关于x轴对称的点的坐标为.16. 已知关于x的函数y=(n-2)x|n|-1-6是一次函数,则n的值为.17. 如图,已知一次函数y1=kx-b与y2=nx函数图象相交于点M,当kx-b=nx时,x的值是 , 当y1>y2时,x的取值范围是 , 当y1<y2时,x的取值范围是.
 18. 如图,在长方形ABCD中,AB=8,GC= , AE平分∠BAG交BC于点E,E是BC的中点,则AG的长为.
18. 如图,在长方形ABCD中,AB=8,GC= , AE平分∠BAG交BC于点E,E是BC的中点,则AG的长为.
三、解答题:(共8小题,满分66分.)
-
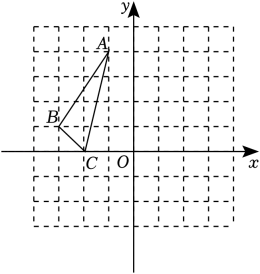
19. 如图,请作出△ABC关于y轴对称的△A1B1C1 , 并写出点A1、B1、C1的坐标.
 20. 如图:已知在△ABC中,AD平分∠BAC,AE⊥BC,垂足为E,∠B=38°,∠C=70°,求∠DAE的度数.
20. 如图:已知在△ABC中,AD平分∠BAC,AE⊥BC,垂足为E,∠B=38°,∠C=70°,求∠DAE的度数.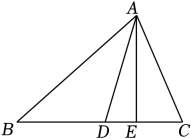 21. 已知一次函数的图象经过A(2,0),B(0,4)两点.(1)、求此一次函数表达式;(2)、试判断点(-1,6)是否在此一次函数的图象上.22. 如图,点B、F、C、E在同一条直线上,AB⊥BE,DE⊥BE,AB=DE,BF=EC,求证:∠A=∠D.
21. 已知一次函数的图象经过A(2,0),B(0,4)两点.(1)、求此一次函数表达式;(2)、试判断点(-1,6)是否在此一次函数的图象上.22. 如图,点B、F、C、E在同一条直线上,AB⊥BE,DE⊥BE,AB=DE,BF=EC,求证:∠A=∠D. 23. 欢欢和父亲起设计一个三角形屋架,如图,父亲给出一组数据:AB=AC=7m,BD=CE=2.5m,AD=4m,∠DAE=60°,让欢欢根据这组数据计算制作这个三角形屋架一共需要多长的钢材,请你帮欢欢计算一下,并说明理由.
23. 欢欢和父亲起设计一个三角形屋架,如图,父亲给出一组数据:AB=AC=7m,BD=CE=2.5m,AD=4m,∠DAE=60°,让欢欢根据这组数据计算制作这个三角形屋架一共需要多长的钢材,请你帮欢欢计算一下,并说明理由. 24. 如图,在△ABC中,AB=AC,CE=6,直线ED是线段AC的垂直平分线,∠BAC=120°,求线段BE的长.
24. 如图,在△ABC中,AB=AC,CE=6,直线ED是线段AC的垂直平分线,∠BAC=120°,求线段BE的长.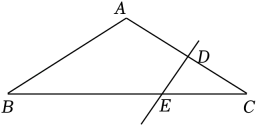 25. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.
25. 如图,AD=BD,∠CAD+∠CBD=180°,求证:CD平分∠ACB.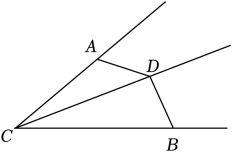 26. 我区应国家号召,认真贯彻落实党的二十大精神,全面推进乡村振兴,把富民政策一项一项落实好,特将农户种植的农产品包装成A、B两种大礼包.某超市预购进两种大礼包共400个,两种大礼包的进价和预售价如表.设购进A种大礼包x个,且所购进的两种大礼包能全部卖完时获得的总利润为W元.
26. 我区应国家号召,认真贯彻落实党的二十大精神,全面推进乡村振兴,把富民政策一项一项落实好,特将农户种植的农产品包装成A、B两种大礼包.某超市预购进两种大礼包共400个,两种大礼包的进价和预售价如表.设购进A种大礼包x个,且所购进的两种大礼包能全部卖完时获得的总利润为W元.大礼包类型
进价/(元/个)
售价/(元/个)
A
47
65
B
37
50
(1)、求W关于x的函数表达式(不要求写x的取值范围);(2)、如果购进两种大礼包的总费用不超过18000元,那么商场如何进货才能获得最大利润?最大利润是多少?