广西贵港市平南县2022-2023学年八年级上学期期末数学试卷

试卷更新日期：2023-01-07 类型：期末考试

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）

1. 在 $- \frac{1}{2}$ ， $\frac{22}{7}$ ， $\sqrt{2}$ ， 2022这四个数中，无理数是（）

A、 $- \frac{1}{2}$ B、 $\frac{22}{7}$ C、 $\sqrt{2}$ D、2022

查看试题解析
2. 若分式 $\frac{| x | - 1}{x + 1}$ 的值为零，则x的值是（）

A、1 B、﹣1 C、±1 D、2

查看试题解析
3. 下列长度的三条线段首尾相接不能围成三角形的是（）

A、2，3，4 B、8，7，15 C、6，8，10 D、13，12，20

查看试题解析
4. 下列计算正确的是（）

A、2 $\sqrt{3}$ +3 $\sqrt{2}$ ＝5 B、 $\frac{a - b}{a + b}$ ＝ $\frac{b - a}{b + a}$ C、（- $\frac{y^{3}}{x^{2}}$ ）³＝ $\frac{y^{6}}{x^{9}}$ D、x²•3x^-3＝ $\frac{3}{x}$

查看试题解析
5. 若a＞b，则下列不等式中，错误的是（）

A、3a＞3b B、- $\frac{a}{3}$ ＜- $\frac{b}{3}$ C、4a-3＞4b-3 D、ac²＞bc²

查看试题解析
6. 估计 $\sqrt{32}$ × $\sqrt{\frac{1}{2}}$ + $\sqrt{20}$ 的运算结果应在（　　）

A、6到7之间 B、7到8之间 C、8到9之间 D、9到10之间

查看试题解析
7. 下列说法正确的是（）

A、 $\sqrt{81}$ 的平方根是±3 B、三个角分别相等的两个三角形全等 C、带根号的数都是无理数 D、8的立方根是2，即 $\sqrt{8}$ ＝2

查看试题解析
8. 数轴上表示1， $\sqrt{2}$ 的对应点分别为A，B，点B关于点A的对称点为C，则点C所表示的数是（）

A、 $\sqrt{2}$ ﹣1 B、1﹣ $\sqrt{2}$ C、2﹣ $\sqrt{2}$ D、 $\sqrt{2}$ ﹣2

查看试题解析
9. 在△ABC中，∠A＝60°，直线MN∥BC，MN分别与AB，AC相交于点D，E，若∠ADM＝139°，则∠C的度数是（）

A、75° B、79° C、81° D、83°

查看试题解析
10. 《九章算术》中有一道关于古代驿站送信的题目，其白话译文为：一份文件，若用慢马送到800里远的城市，所需时间比规定时间多1天；若改为快马派送，则所需时间比规定时间少2天，已知快马的速度是慢马的 $\frac{5}{2}$ 倍，求规定时间.设规定时间为x天，则下列列出的分式方程正确的是（）

A、 $\frac{800}{x + 2} = \frac{5}{2} \times \frac{800}{x - 1}$ B、 $\frac{800}{x - 2} = \frac{5}{2} \times \frac{800}{x + 1}$ C、 $\frac{800}{x - 1} = \frac{5}{2} \times \frac{800}{x + 2}$ D、 $\frac{800}{x + 1} = \frac{5}{2} \times \frac{800}{x - 2}$

查看试题解析
11. 若分式方程 $\frac{x - a}{x + 2}$ ＝a无解，则a的值是（）

A、1 B、-2 C、-1或2 D、1或-2

查看试题解析
12. 如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ，下列结论错误的是（）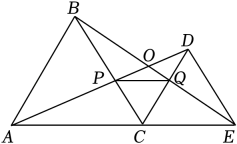

A、AD＝BE B、∠DOE＝60° C、DE＝DP D、PQ∥AE

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

13. 若二次根式 $\sqrt{3 - x}$ 有意义，则 x 的取值范围是．

查看试题解析
14. 用科学记数法表示的数-2.6×10^-5写成小数是.

查看试题解析
15. “x的2倍与y的和不大于2”用不等式可表示为.

查看试题解析
16. 如图，在△ABC中，DE是AC的垂直平分线，AE＝3cm，△ABD的周长为12cm，则△ABC的周长是.

查看试题解析
17. 若不等式组 ${\begin{array}{l} x > a \\ 2 x + 1 < 3 \end{array}$ 的解集中共有3个整数解，则a的取值范围是.

查看试题解析
18. 在进行二次根式化简时，我们可以将 $\frac{2}{\sqrt{3} + 1}$ 进一步化简，如：
$\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$

则 $\frac{2}{1 + \sqrt{5}} + \frac{2}{\sqrt{5} + \sqrt{9}} + \frac{2}{\sqrt{9} + \sqrt{13}} + \dots + \frac{2}{\sqrt{4 n - 1} + \sqrt{4 n + 3}}$ ＝.

查看试题解析

三、解答题（本大题共8小题，满分66分.解答应写出文字说明、证明过程或演算步骤.）

19. 计算：

(1)、（ $\frac{1}{3}$ ）^-2+（π-2022）⁰- $\sqrt{9}$ +|2- $\sqrt{5}$ |.

(2)、 $\sqrt{24}$ ÷ $\sqrt{1 \frac{1}{2}}$ - $\sqrt{\frac{1}{3}}$ × $\sqrt{12}$ + $\sqrt{48}$ .

查看试题解析
20. 解分式方程： $\frac{3 + x}{x - 3}$ -1＝ $\frac{2}{x}$ .

查看试题解析
21. 解不等式组： ${\begin{cases} 5 x - 1 \leq 3 (x + 1) \\ \frac{2 x - 1}{3} - \frac{2 x + 3}{2} < - 1 \end{cases}$ ，并利用数轴表示不等式组的解集.

查看试题解析
22. 尺规作图（保留作图痕迹，不要求写出作法）.
如图，在△ABC中，AC＝BC.

(1)、求作线段AB的垂直平分线，与AB相交于点E，过点B作AC所在直线的垂线，与直线AC相交于点D.

(2)、若∠A＝32°，求∠CBD的度数.

查看试题解析
23. 先化简，再求值： $\frac{x + 2}{x^{2} - 2 x}$ ÷（ $\frac{8 x}{x - 2}$ +x-2），其中x＝ $\sqrt{2}$ -1.

查看试题解析
24. 如图，在等腰△ABC中，∠BAC＝90°，D是BC边上任一点，CE⊥AD于E，BF⊥AD交AD的延长线于F，AH⊥BC于H，交CE于G；求证：BD＝AG.

查看试题解析
25. 某公司需将一批材料运往工厂，计划租用甲、乙两种型号的货车，在每辆货车都满载的情况下，甲型货车每辆装载量是乙型货车的 $\frac{5}{3}$ 倍，若甲、乙两种型号货车各装载1500箱材料，甲型货车比乙型货车少用40辆.

(1)、甲、乙两种型号的货车每辆分别可装载多少箱材料？

(2)、经初步估算，公司要运往工厂的这批材料不超过1110箱.计划租用甲、乙两种型号的货车共60辆，且乙型货车的数量不大于甲型货车数量的2倍，该公司一次性将这批材料运往工厂共有哪几种租车方案？

查看试题解析
26. 在四边形ABCD中.

(1)、如图1，AB＝AD，∠ABC＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠DAB，探究图中EF，BE，DF之间的数量关系.
小林同学探究此问题的方法是：延长CB到点G，使BG＝DF.连接AG，先对比△ABG与△ADF的关系，再对比△AEF与△AEG的关系，可得出EF、BE、DF之间的数量关系，他的结论是；

(2)、如图2，在四边形ABCD中，AB＝AD，∠B+∠ADF＝180°，E、F分别是BC，CD上的点，且∠EAF＝ $\frac{1}{2}$ ∠DAB，则上述结论是否仍然成立，请说明理由.

(3)、如图3，在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD，若点F在CB的延长线上，点E在CD的延长线上，若EF＝BF+DE，请写出∠EAF与∠DAB的数量关系，并给出证明过程.

查看试题解析