2023年中考数学精选真题实战测试13 一元一次不等式(组)A
试卷更新日期:2023-01-07 类型:二轮复习
一、单选题(每题3分,共30分)
-
1. 若 , 则下列不等式中正确的是( )A、 B、 C、 D、2. 若x=2是下列四个选项中的某个不等式组的一个解,则这个不等式组是( )A、 B、 C、 D、3. 如果点P(m,1+2m)在第三象限内,那么m的取值范围是( )A、 B、 C、 D、4. 不等式组 , 的解集是( )A、 B、无解 C、 D、5. 关于 , 的方程组的解中与的和不小于5,则的取值范围为( )A、 B、 C、 D、6. 把不等式组中每个不等式的解集在同一条数轴上表示出来,正确的为( )A、
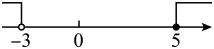 B、
B、 C、
C、 D、
D、 7. 已知a,b,c,d是实数,若a>b,c=d,则( )A、a+c>b+d B、a+b>c+d C、a+c>b-d D、a+b>c-d8. 若关于x的一元一次不等式组 的解集为 ,且关于y的分式方程 的解是负整数,则所有满足条件的整数a的值之和是( )A、-26 B、-24 C、-15 D、-139. 关于x的分式方程 的解为正数,且关于y的不等式组 的解集为y≥5,则所有满足条件的整数a的值之和是( )A、13 B、15 C、18 D、2010. 已知关于x的分式方程无解,且关于y的不等式组有且只有三个偶数解,则符合条件的整数m有( )个.A、0 B、1 C、2 D、3
7. 已知a,b,c,d是实数,若a>b,c=d,则( )A、a+c>b+d B、a+b>c+d C、a+c>b-d D、a+b>c-d8. 若关于x的一元一次不等式组 的解集为 ,且关于y的分式方程 的解是负整数,则所有满足条件的整数a的值之和是( )A、-26 B、-24 C、-15 D、-139. 关于x的分式方程 的解为正数,且关于y的不等式组 的解集为y≥5,则所有满足条件的整数a的值之和是( )A、13 B、15 C、18 D、2010. 已知关于x的分式方程无解,且关于y的不等式组有且只有三个偶数解,则符合条件的整数m有( )个.A、0 B、1 C、2 D、3二、填空题(每空3分,共18分)
-
11. 如果一元一次方程的解是一元一次不等式组的解.则称该一元一次方程为该一元一次不等式组的关联方程.若方程是关于x的不等式组的关联方程,则n的取值范围是 .12. 不等式组的所有整数解的和为.13. 若关于x的一元一次不等式组的解集为 , 则a的取值范围是 .14. 某品牌护眼灯的进价为240元,商店以320元的价格出售.“五一节”期间,商店为让利于顾客,计划以利润率不低于20%的价格降价出售,则该护眼灯最多可降价元.
 15. 关于x的不等式组 恰有3个整数解,则a的取值范围是.16. 已知关于x的不等式组无解,则的取值范围是 .
15. 关于x的不等式组 恰有3个整数解,则a的取值范围是.16. 已知关于x的不等式组无解,则的取值范围是 .三、解答题(共9题,共72分)
-
17. 在下面给出的三个不等式中,请你任选两个组成一个不等式组,解这个不等式组,并把解集表示在数轴上.
①2x﹣1<7;②5x﹣2>3(x+1);③x+3≥1﹣x.
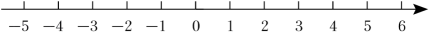 18. 求不等式组的解集.19. 求不等式组的解集,并把它的解集表示在数轴上.20. 解不等式组并将其解集在数轴上表示出来.
18. 求不等式组的解集.19. 求不等式组的解集,并把它的解集表示在数轴上.20. 解不等式组并将其解集在数轴上表示出来.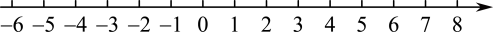 21. 阅读材料:若点 , 在数轴上分别表示实数 , , 那么 , 之间的距离可表示为.例如 , 即表示3,1在数轴上对应的两点之间的距离;同样:表示5,在数轴上对应的两点之间的距离.根据以上信息,完成下列题目:(1)、已知 , , 为数轴上三点,点对应的数为 , 点对应的数为1.
21. 阅读材料:若点 , 在数轴上分别表示实数 , , 那么 , 之间的距离可表示为.例如 , 即表示3,1在数轴上对应的两点之间的距离;同样:表示5,在数轴上对应的两点之间的距离.根据以上信息,完成下列题目:(1)、已知 , , 为数轴上三点,点对应的数为 , 点对应的数为1.①若点对应的数为 , 则 , 两点之间的距离为 ;
②若点到点的距离与点到点的距离相等,则点对应的数是 .
(2)、对于这个代数式.①它的最小值为 ;
②若 , 则的最大值为 .
22. 金师傅近期准备换车,看中了价格相同的两款国产车.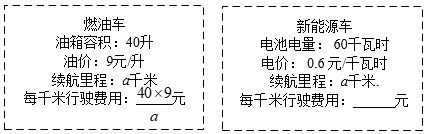 (1)、用含a的代数式表示新能源车的每千米行驶费用.(2)、若燃油车的每千米行驶费用比新能源车多0.54元.
(1)、用含a的代数式表示新能源车的每千米行驶费用.(2)、若燃油车的每千米行驶费用比新能源车多0.54元.①分别求出这两款车的每千米行驶费用.
②若燃油车和新能源车每年的其它费用分别为4800元和7500元.问:每年行驶里程为多少千米时,买新能源车的年费用更低?(年费用=年行驶费用+年其它费用)
23. 钢钢准备在重阳节购买鲜花到敬老院看望老人,现将自己在劳动课上制作的竹篮和陶罐拿到学校的“跳蚤市场”出售,以下是购买者的出价: (1)、根据对话内容,求钢钢出售的竹篮和陶罐数量;(2)、钢钢接受了钟钟的报价,交易后到花店购买单价为5元/束的鲜花,剩余的钱不超过20元,求有哪几种购买方案.24. 学校开展大课间活动,某班需要购买A、B两种跳绳.已知购进10根A种跳绳和5根B种跳绳共需175元:购进15根A种跳绳和10根B种跳绳共需300元.(1)、求购进一根A种跳绳和一根B种跳绳各需多少元?(2)、设购买A种跳绳m根,若班级计划购买A、B两种跳绳共45根,所花费用不少于548元且不多于560元,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?25. 去年防洪期间,某部门从超市购买了一批数量相等的雨衣(单位:件)和雨鞋(单位:双),其中购买雨衣用了400元,购买雨鞋用了350元,已知每件雨衣比每双雨鞋贵5元.(1)、求每件雨衣和每双雨鞋各多少元?(2)、为支持今年防洪工作,该超市今年的雨衣和雨鞋单价在去年的基础上均下降了20%,并按套(即一件雨衣和一双雨鞋为一套)优惠销售. 优惠方案为:若一次购买不超过5套,则每套打九折:若一次购买超过5套,则前5套打九折,超过部分每套打八折.设今年该部门购买了a套,购买费用为W元,请写出W关于a的函数关系式.(3)、在(2)的情况下,今年该部门购买费用不超过320元时最多可购买多少套?
(1)、根据对话内容,求钢钢出售的竹篮和陶罐数量;(2)、钢钢接受了钟钟的报价,交易后到花店购买单价为5元/束的鲜花,剩余的钱不超过20元,求有哪几种购买方案.24. 学校开展大课间活动,某班需要购买A、B两种跳绳.已知购进10根A种跳绳和5根B种跳绳共需175元:购进15根A种跳绳和10根B种跳绳共需300元.(1)、求购进一根A种跳绳和一根B种跳绳各需多少元?(2)、设购买A种跳绳m根,若班级计划购买A、B两种跳绳共45根,所花费用不少于548元且不多于560元,则有哪几种购买方案?(3)、在(2)的条件下,哪种购买方案需要的总费用最少?最少费用是多少元?25. 去年防洪期间,某部门从超市购买了一批数量相等的雨衣(单位:件)和雨鞋(单位:双),其中购买雨衣用了400元,购买雨鞋用了350元,已知每件雨衣比每双雨鞋贵5元.(1)、求每件雨衣和每双雨鞋各多少元?(2)、为支持今年防洪工作,该超市今年的雨衣和雨鞋单价在去年的基础上均下降了20%,并按套(即一件雨衣和一双雨鞋为一套)优惠销售. 优惠方案为:若一次购买不超过5套,则每套打九折:若一次购买超过5套,则前5套打九折,超过部分每套打八折.设今年该部门购买了a套,购买费用为W元,请写出W关于a的函数关系式.(3)、在(2)的情况下,今年该部门购买费用不超过320元时最多可购买多少套?