华师大版备考2023中考数学二轮复习 专题39 探索图形的规律

试卷更新日期：2023-01-06 类型：二轮复习

进入 出卷网 下载

一、单选题

  • 1. 将一些完全相同的梅花按如图所示的规律摆放，第1个图形有5朵梅花，第2个图形有8朵梅花，第3个图形有13朵梅花，…按此规律，则第7个图形中共有梅花的朵数是（    ）

    A、39 B、40 C、53 D、68

    查看试题解析

  • 2. 边长为一个单位的正方形ABCD纸片在数轴上的位置如图所示，点A ，D对应的数分别为正方形ABCD纸片绕着顶点在数轴上向右滚动(动)滚动过程中经过数轴上的数2022的顶点是（ ）

    A、点A B、点B C、点C D、点D

    查看试题解析

  • 3. 腾讯公司将QQ等级采用“满四进一”∶一开始是星星(一个星星为1级），4个星星等于一个月亮， 4 个月亮等于一个太阳，4 个太阳等于一个皇冠.如图，这位用户的QQ等级为（    ）

    A、7 级 B、20 级 C、78 级 D、94 级

    查看试题解析

  • 4. 等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和-1，若△ABC绕顶点沿顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2020次后，点B（ ）

    A、不对应任何数 B、对应的数是2018 C、对应的数是2019 D、对应的数是2020

    查看试题解析

  • 5. 如图，在平面直角坐标系中，设一质点M自P0（1，0）处向上运动1个单位P1（1，1），然后向左运动2个单位至P2处，再向下运动3个单位至P3处，再向右运动4个单位至P4处，再向上运动5个单位至P5处……如此继续运动下去，则P2022的坐标为（  ）

    A、（-1011，1011） B、（505，-504） C、（504，-505） D、（1011，1011）

    查看试题解析

  • 6. 如图，等边三角形的顶点A(1 ， 1)、B(3 ， 1) ， 规定把等边△ABC先沿x轴翻折，再向右平移1个单位为一次交换，如果这样连续经过100次变换后，等边△ABC的顶点C的坐标为（    ）

    A、(99 ， −3−1) B、(100 ， 3+1) C、(101 ， −3−1) D、(102 ， 3+1)

    查看试题解析

  • 7. 观察下列图形，则第2022个图形中三角形的个数是（   ）

    A、8084 B、8088 C、2021 D、2022

    查看试题解析

  • 8. 在《九章算术注》中用不同颜色的算筹（小棍形状的记数工具）分别表示正数和负数（白色为正，黑色为负），如图1表示的是+21−32=−11的计算过程，则图2表示的过程是在计算（    ）

    A、(−13)+(+23)=10 B、(−31)+(+32)=1 C、(+13)+(+23)=36 D、(+13)+(−23)=−10

    查看试题解析

  • 9. 在如图所示的平面直角坐标系中，有一个由等边三角形ABC和以AB为直径的半圆组成的“冰淇淋”形图案，且点A、B在x轴上，点C在y轴上，AB=4 ， 过点A作AD⊥AC交半圆于点D ， 将该“冰淇淋”形图案绕点C逆时针旋转，每次旋转45° ， 则第98次旋转结束时，点D的坐标是（ ）

    A、(−23 ， −2) B、(−33 ， 1+23) C、(1 ， 3) D、(−33 ， −1−23)

    查看试题解析

  • 10. 如图，直线 l1 ： y=x+1 与直线 l2 ： y=x2+12 相交于点 P ，直线 l1 与 y 轴交于点 A ，一动点 C 从点 A 出发，先沿平行于 x 轴 方向运动，到达直线 l2 上的点 B1 处后，改为垂直于 x 轴的方向运动，到达直线 l1 上的点 A1 处后，再沿平行于 x 轴的方向运动，到达直线 l2 上的点 B2 处后，又改为垂直于 x 轴的方向运动，到达直线 l1 上的点 A2 处后，仍沿平行于 x 轴的方向运动…照此规律运动，动点 C 依次经过点 B1 ， A1 ， B2 ， A2 ， B3 ， A3 ， B2020 ， A2020 …则 A2022B2022 的长度为（    ）

    A、22021 B、22022 C、2022 D、4044

    查看试题解析

二、填空题

  • 11. 小明按照如图的方法用灰色和白色的小正方形摆图形.当中间摆2022个灰色的小正方形时，四周共需要摆白色小正方形的个数为.

    查看试题解析

  • 12.  如图，用黑白两种颜色的菱形纸片，按黑色片数逐渐增加1的规律拼成下列图案，若第n个图案中有2023个白色纸片，则n的值为.

    查看试题解析

  • 13. 数轴上表示整数的点称为整点，某数轴的单位长度是1厘米，若在这个数轴上随意画出一条长2022厘米的线段AB，则线段AB盖住的整点共有个．

    查看试题解析

  • 14. 如图，点A1、A2、A3、…、An在抛物线y=x2图象上，点B1、B2、B3、…、Bn在y轴上，若△A1B0B1、△A2B1B2、…、△AnBn-1Bn都为等腰直角三角形（点B0是坐标原点），则△A2018B2017B2018的底边长为 ．

    查看试题解析

  • 15. 如图，△A1B1C1中，A1B1＝4，A1C1＝5，B1C1＝7．点A2 ， B2 ， C2分别是边B1C1 ， A1C1 ， A1B1的中点；点A3 ， B3 ， C3分别是边B2C2 ， A2C2 ， A2B2的中点；…以此类推，则△A2022B2022C2022的周长是 ．

    查看试题解析

  • 16. 如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点(1 ， 1) ， 第2次接着运动到点(2 ， 0) ， 第3次接着运动到点(3 ， 2) ， ……按这样的规律第13次运动到点的坐标；经过第2022次运动后，动点P的坐标 ．

    查看试题解析

  • 17. 如图，在矩形ABCD中，AB=2 ， CB=4 ， 连接AC ， 以对角线AC为边，按逆时针方向作矩形ACC1B1 ， 使矩形ACC1B1∽矩形ADCB；再连接AC1 ， 以对角线AC1为边，按逆时针方向作矩形AC1C2B2 ， 使矩形AC1C2B2∽矩形ACC1B1 ， …，按照此规律作下去．若矩形ABCD的面积记作S1 ， 矩形ACC1B1的面积记作S2 ， 矩形AC1C2B2的面积记作S3 ， …，则S2022的值为 ．

    查看试题解析

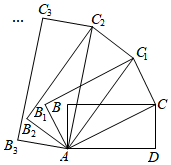
三、解答题

  • 18.
    按如图方式摆放餐桌和椅子．用x来表示餐桌的张数，用y来表示可坐人数． 

     ①题中有几个变量？ 

     ②你能写出两个变量之间的关系吗？ 

     

    查看试题解析

  • 19. 如图所示，由一些点组成形如三角形的图形，每条“边”（包括两个顶点）有 n(n>1) 个点，每个图形的总点数记为S ．

    (1)、当 n=4 时，S的值为；当 n=6 时，S的值为；
    (2)、每条“边”有n个点时的总点数S是（用含n的式子表示）；
    (3)、当 n=2021 时，总点数S是多少？

    查看试题解析

四、综合题

  • 20.         
    (1)、把一堆黑色棋子按如图1所示的规律排列起来，摆成第n个“口”需要a枚黑色的棋子，请用含n的代数式表示：a=

    图1；

    (2)、把一堆黑色和白色棋子按如图2所示的规律排列起来：

    求：从前往后数，第2018颗棋子的颜色。

    (3)、把一堆黑色和白色棋子被按如图3所示的规律排列起来：

    若图3中的黑色棋子全部由图1中的a枚黑色棋子充当，用完为止（黑色棋子共有a枚），按照这样的规律摆放至以黑色棋子收尾。当a=100，请列式并计算：这时，图3中黑白棋子的总数是多少？

    查看试题解析

  • 21. 如图，每张小纸带的长为40cm，用胶水把它们粘贴成一张长纸带，接头粘贴重叠部分的长为3cm．

    (1)、用2张这样的小纸带粘贴成的纸带的长度为77cm，则用3张这样的小纸带粘贴成的纸带的长度为cm．
    (2)、①用n张这样的小纸带粘贴成的纸带的长度是  ▲  cm；

    ②计算用20张这样的小纸带粘贴成的纸带的长度．

    查看试题解析

  • 22. 将边长相等的黑、白两色小正方形按如图所示的方式拼接起来，第1个图由5个白色小正方形和1个黑色小正方形拼接起来；第2个图由8个白色小正方形和2个黑色小正方形拼接起来；第3个图由11个白色小正方形和3个黑色小正方形拼接起来，依此规律拼接．

    (1)、第4个图白色小正方形的个数为个；第8个图白色小正方形的个数为个；
    (2)、第n个图白色小正方形的个数为个；
    (3)、白色小正方形的个数为6068个，是第个图形；
    (4)、是否存在某个图形，其白色小正方形的个数为2031个，若存在，求出是第几个图形；若不存在，请说明理由．

    查看试题解析