华师大版备考2023中考数学二轮复习专题37 定义新运算

试卷更新日期：2023-01-06 类型：二轮复习

进入出卷网下载

一、单选题

1. 新定义运算： $m * n = m n^{2} - 2 n - 1$ ，则方程 $- 1 * x = 0$ 的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断

查看试题解析
2. 已知两圆相交，当每个圆的圆心都在在另一个圆的圆外时，我们称此两圆的位置关系为“外相交”．已知两圆“外相交”，且半径分别为2和5，则圆心距的取值可以是（）

A、4 B、5 C、6 D、7

查看试题解析
3. 定义新运算“⊕”如下：当a＞b时，a⊕b＝ab+b；当a＜b时，a⊕b＝ab-b，若3⊕（x+2）＞0，则x的取值范围是（）

A、-1＜x＜1或x＜-2 B、x＜-2或1＜x＜2 C、-2＜x＜1或x＞1 D、x＜-2或x＞2

查看试题解析
4. 设[a]是有理数，用[a]表示不超过a的最大整数，如[1.7]＝1，[﹣1]＝﹣1，[0]＝0，[﹣1.2]＝﹣2，则在以下四个结论中，正确的是（）

A、[a]+[﹣a]＝0 B、[a]+[﹣a]=0或﹣1 C、[a]+[﹣a]≠0 D、[a]+[﹣a]=0或1

查看试题解析
5. 若规定“!”是一种数学运算符号，且1!＝1，2!＝2×1＝2，4!＝4×3×2×1＝24，…，则 $\frac{100!}{98!}$ 的值为（）

A、9900 B、99! C、 $\frac{50}{49}$ D、2

查看试题解析
6. 已知点P的坐标为（a，b），其中a，b均为实数，若a，b满足3a＝2b+5，则称点P为“和谐点”．若点M（m﹣1，3m+2）是“和谐点”，则点M所在的象限是（）

A、第四象限 B、第三象限 C、第二象限 D、第一象限

查看试题解析
7. 将4个数 $a$ ， $b$ ， $c$ ， $d$ 排成2行、2列，两边各加一条竖线，记成 $|\begin{matrix} a & b \\ c & d \end{matrix}|$ ，并规定 $|\begin{matrix} a & b \\ c & d \end{matrix}| = a d - b c .$ 例如 $|\begin{matrix} 2 & 4 \\ 1 & 3 \end{matrix}| = 2 \times 3 - 4 \times 1 = 2$ ，则 $|\begin{matrix} x & 3 \\ x & x - 1 \end{matrix}| = - 3$ 的根的情况为（）

A、只有一个实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、没有实数根

查看试题解析
8. 函数 $y = [x]$ 叫做高斯函数，其中x为任意实数， $[x]$ 表示不超过x的最大整数．定义 ${x} = x - [x]$ ，则下列说法正确的个数为（）
① $[- 4.1] = - 4$ ；
② ${3.5} = 0.5$ ；
③高斯函数 $y = [x]$ 中，当 $y = - 3$ 时，x的取值范围是 $- 3 \leq x < - 2$ ；
④函数 $y = {x}$ 中，当 $2.5 < x \leq 3.5$ 时， $0 \leq y < 1$ ．

A、0 B、1 C、2 D、3

查看试题解析
9. 对多项式x-y-z-m-n任意加括号后仍然只含减法运算并将所得式子化简，称之为“加算操作”，例如：(x-y)-(z-m-n)=x-y-z+m+n，x-y-(z-m)-n = x-y-z+m-n，……，
给出下列说法：

①至少存在一种“加算操作”，使其结果与原多项式相等； ②不存在任何“加算操作”，使其结果与原多项式之和为0； ③所有的“加算操作”共有 8 种不同的结果．以上说法中正确的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
10. 定义：平面直角坐标系中，点 $P (x ， y)$ 的横坐标x的绝对值表示为 $| x |$ ，纵坐标y的绝对值表示为 $| y |$ ，我们把点 $P (x ， y)$ 的横坐标与纵坐标的绝对值之和叫做点 $P (x ， y)$ 的折线距离，记为 $| M | = | x | + | y |$ （其中的“＋”是四则运算中的加法），若抛物线 $y = a x^{2} + b x + 1$ 与直线 $y = x$ 只有一个交点M，已知点M在第一象限，且 $2 \leq | M | \leq 4$ ，令 $t = 2 b^{2} - 4 a + 2022$ ，则t的取值范围为（）

A、 $2018 \leq t \leq 2019$ B、 $2019 \leq t \leq 2020$ C、 $2020 \leq t \leq 2021$ D、 $2021 \leq t \leq 2022$

查看试题解析

二、填空题

11. 定义一种运算： $a * b = 2 a b + a - b$ ，则 $(- 3) * 5 =$ 。

查看试题解析
12. 对于有理数 $x 、 y$ 定义了一种新运算“*”，规定： $x * y = x y - x - y$ ，例如：
$1 * 2 = 1 \times 2 - 1 - 2 = - 1$ ， $2 * (- 3) = 2 \times (- 3) - 2 - (- 3) = - 5$ ，若 $x * \frac{1}{2} = 1 * 2 x$ ，那么 $x =$ ．

查看试题解析
13. 定义 $a - b = 0$ ，则称 $a$ 、 $b$ 互容，若 $2 x^{2} - 2$ 与 $x + 4$ 互容，则 $6 x^{2} - 3 x - 9 =$ ．

查看试题解析
14. 定义新运算“*”为： $a^{*} b = {\begin{array}{l} a - b & (a ⩾ b) \\ 3 b & (a < b) \end{array}$ ，则当 $x = 3$ 时，计算 $2^{*} x - 4 * x$ 的结果为。

查看试题解析
15. 如果关于 $x$ 的方程 $[\frac{x}{2}] + [\frac{2 x}{3}] + [\frac{3 x}{5}] = \frac{k}{7} x$ 有正整数解，那么正整数 $k$ 的所有可能取值之和为．

查看试题解析
16. 我们把对非负数x “四舍五入”到个位的值记为 $《 x 》$ ，即当n为非负整数时，若 $n - \frac{1}{2} \leq x < n + \frac{1}{2}$ ，则 $《 x 》 = n$ ，例如 $《 0.67 》 = 1 ，《 2.49 》 = 2 ，$ 下列结论中：① $《 2 x 》 = 2 《 x 》$ ；②当m为非负整数时， $《 m + 2 x 》 = m + 《 2 x 》$ ；③满足 $《 x 》 = \frac{3}{2} x$ 的非负整数x只有两个．其中结论正确的是(填序号)

查看试题解析

三、解答题

17. 约定：上方相邻两数之和等于这两数下方箭头共同指向的数．

示例：即 $4 + 3 = 7$ ．

如图，当 $x = 2$ ， $y = - \frac{6}{5}$ 号时，求Z的值．

查看试题解析
18. 用※定义一种新运算：对于任意实数m和n，规定m※n＝ $m^{2} n － m n － 3 n$ ．如：1※2 $= 1^{2} \times 2 － 1 \times 2 － 3 \times 2 = － 6$ ．求（－2）※ $\sqrt{3}$ 值．

查看试题解析
19. 定义新运算：对于任意实数m，n都有m☆n＝m²n＋n，等式右边是常用的加法、减法、乘法及乘方运算. 例如：－3☆2＝(－3)²×2＋2＝20.根据以上知识解决问题：若2☆a的值小于0，请判断方程：2x²－bx＋a＝0的根的情况.

查看试题解析

四、综合题

20. 在平面直角坐标系中，若点P的坐标为（x，y），则定义：d（x，y）＝|x|+|y|为点P到坐标原点O的“折线距离”.

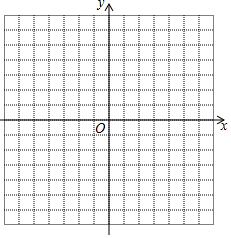(1)、若已知P（-2，3），则点P到坐标原点O的“折线距离”d（-2，3）＝；

(2)、若点P（x，y）满足2x+y＝0，且点P到坐标原点O的“折线距离”d（x，y）＝6，求出P的坐标；

(3)、若点P到坐标原点O的“折线距离”d（x，y）＝3，试在坐标系内画出所有满足条件的点P构成的图形，并求出该图形的所围成封闭区域的面积.

查看试题解析
21. 对于平面直角坐标系中的任意两点P₁（x₁ ， y₁），P₂（x₂ ， y₂），我们把|x₁-x₂|+|y₁-y₂|叫做P₁、P₂两点间的直角距离，记作d（P₁ ， P₂）.

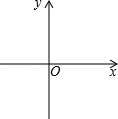(1)、令P₀（2，-3），O为坐标原点，则d（O，P₀）＝；

(2)、已知O为坐标原点，动点P（x，y）满足d（O，P）＝1，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P所组成的图形；

(3)、设P₀（x₀ ， y₀）是一定点，Q（x，y）是直线y＝ax+b上的动点，我们把d（P₀ ， Q）的最小值叫做P₀到直线y＝ax+b的直角距离. 若P（a，-3）到直线y＝x+1的直角距离为6，求a的值.

查看试题解析
22. 阅读材料：
我们定义：如果两个实数的差等于这两个实数的商，那么这两个实数就叫做“差商等数对”．即：如果 $a - b = a \div b$ ，那么α与b就叫做“差商等数对”，记为 $(a ， b)$ ．例如： $4 - 2 = 4 \div 2$ ； $\frac{9}{2} - 3 = \frac{9}{2} \div 3$ ；则称数对 $(4 ， 2)$ ， $(\frac{9}{2} ， 3)$ 是“差商等数对”．
根据上述材料，解决下列问题：

(1)、下列数对中，“差商等数对”是（填序号）；
① $(- 8.1 ， - 9)$ ② $(\frac{1}{2} ， \frac{1}{2})$ ③ $(- \frac{1}{2} ， - 1)$

(2)、如果 $(a ， 2)$ 是“差商等数对”，请求出a的值；

(3)、在（2）的条件下，先化简再求值： $[(4 a^{2} b - 2 a b^{2} - b^{3}) \div b - (2 a + b) (2 a - b)] \div \frac{2}{3} b$ ．

查看试题解析
23. 我们新定义一种三角形：如果一个三角形两条边的平方和等于第三边平方的4倍，那么这个三角形叫做常态三角形．例如：某三角形三边长分别是4， $\sqrt{20}$ 和8，因为 $4^{2} + 8^{2} = 80 = 4 \times {(\sqrt{20})}^{2}$ ，所以这个三角形是常态三角形．

(1)、若△ABC三边长分别是5，6和8，请判断此三角形是否为常态三角形，并说明理由；

(2)、如图，Rt△ABC中，∠ACB＝90°， BC＝ $\sqrt{7}$ ，点D为AB的中点，连接CD，若△ACD是常态三角形，求AC的长.

查看试题解析

华师大版备考2023中考数学二轮复习 专题37 定义新运算

一、单选题

二、填空题

三、解答题

四、综合题

华师大版备考2023中考数学二轮复习专题37 定义新运算