华师大版备考2023中考数学二轮复习 专题32 平移、旋转问题
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 下列各剪纸图案中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、3. 将点绕原点逆时针旋转90°得到的点的坐标是( )A、 B、 C、 D、4. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )
2. 将点先向右平移5个单位长度,再向下平移6个单位长度得到的点的坐标是( )A、 B、 C、 D、3. 将点绕原点逆时针旋转90°得到的点的坐标是( )A、 B、 C、 D、4. 如图,在方格纸中,将 绕点 按顺时针方向旋转90°后得到 ,则下列四个图形中正确的是( )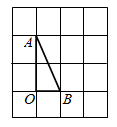 A、
A、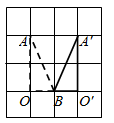 B、
B、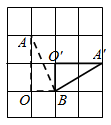 C、
C、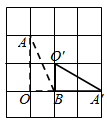 D、
D、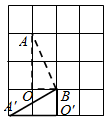 5. 如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( )
5. 如图,在6×4的方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是( ) A、点M B、格点N C、格点P D、格点Q6. 如图 ,已知△ABC 中,∠C=90°,AC=BC= , 将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( )
A、点M B、格点N C、格点P D、格点Q6. 如图 ,已知△ABC 中,∠C=90°,AC=BC= , 将△ABC 绕点 A 顺时针方向旋转 60°得到△A′B′C′的位置,连接 C′B,则 C′B 的长为 ( ) A、2- B、 C、 D、17. 如图,P为正方形内一点, , 将绕点C逆时针旋转得到 , 则的长是( )
A、2- B、 C、 D、17. 如图,P为正方形内一点, , 将绕点C逆时针旋转得到 , 则的长是( ) A、1 B、 C、2 D、8. 如图,正方形ABCD的边长为4, , 点E是直线CM上一个动点,连接BE,线段BE绕点B顺时针旋转45°得到BF,连接DF,则线段DF长度的最小值等于( )
A、1 B、 C、2 D、8. 如图,正方形ABCD的边长为4, , 点E是直线CM上一个动点,连接BE,线段BE绕点B顺时针旋转45°得到BF,连接DF,则线段DF长度的最小值等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知△A′B′O′是由△ABO平移得到的,点A的坐标为(-1,2),它的对应点A'的坐标为(3,4),△ABO内任意一点P(a,b)平移后的对应点P'的坐标为 .10. 在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把绕点B逆时针旋转90°,得 , 点A、O旋转后的对应点为 , , 那么A的长为 .
 11. 如图,把绕点A逆时针旋转 , 得到 , 点恰好落在边AB上,连接 , 则 .
11. 如图,把绕点A逆时针旋转 , 得到 , 点恰好落在边AB上,连接 , 则 . 12. 一个三角板顶点B处刻度为“0”如图1,直角边落在数轴上,刻度“30”和“20”分别与数轴上表示数字-3和-1的点重合,现将该三角板绕着点B顺时针旋转90°,使得另一直角边落在数轴上,此时边上的刻度“15”与数轴上的点P重合,则点P表示的数是.
12. 一个三角板顶点B处刻度为“0”如图1,直角边落在数轴上,刻度“30”和“20”分别与数轴上表示数字-3和-1的点重合,现将该三角板绕着点B顺时针旋转90°,使得另一直角边落在数轴上,此时边上的刻度“15”与数轴上的点P重合,则点P表示的数是. 13. 如图,点A、C分别是y轴、x轴正半轴上的动点、.将线段绕点A顺时针旋转得到线段 , 则的最小值是.
13. 如图,点A、C分别是y轴、x轴正半轴上的动点、.将线段绕点A顺时针旋转得到线段 , 则的最小值是. 14. 如图,中, , , 是边上的中线,把绕点D旋转,点A、B、C分别与点对应,与边交于点E,在旋转过程中,若 , 那么 .
14. 如图,中, , , 是边上的中线,把绕点D旋转,点A、B、C分别与点对应,与边交于点E,在旋转过程中,若 , 那么 . 15. 如图所示,这个图案绕精它的中心旋转α()后能够与它本身重合,则α可以为 (写出一个即可).
15. 如图所示,这个图案绕精它的中心旋转α()后能够与它本身重合,则α可以为 (写出一个即可). 16. 如图,在中, , , , , O为的中点,M为边上一动点,将绕点A逆时针旋转角得到 , 点M的对应点为 , 连接 , 在旋转过程中,线段的长度的最小值是 .
16. 如图,在中, , , , , O为的中点,M为边上一动点,将绕点A逆时针旋转角得到 , 点M的对应点为 , 连接 , 在旋转过程中,线段的长度的最小值是 .
三、作图题
-
17. 如图,已知在平面直角坐标系中,的三个顶点的坐标分别为 , , .

⑴画出关于原点成中心对称的 , 并写出点的坐标;
⑵画出将绕点按顺时针方向旋转所得的并写出点的坐标.
18. 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).画绕点顺时针旋转后的 .
四、解答题
-
19. 如图,在中, , 将绕点A顺时针旋转得到 , 交于点F.若 , 求的长.
 20. 如图,四边形ABCD是正方形.△ABE是等边三角形,M为对角线 BD(不含B,D点)上任意一点,将线段BM绕点B逆时针旋转60°得到BN,连接 EN,AM、CM.请判断线段 AM 和线段 EN 的数量关系,并说明理由.
20. 如图,四边形ABCD是正方形.△ABE是等边三角形,M为对角线 BD(不含B,D点)上任意一点,将线段BM绕点B逆时针旋转60°得到BN,连接 EN,AM、CM.请判断线段 AM 和线段 EN 的数量关系,并说明理由. 21. 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
21. 如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,求BD的长.
五、综合题
-
22. 如图,直线分别与x轴、y轴交于点A、B,点C为线段上一动点(不与A、B重合),以C为顶点作 , 射线交线段于点D,将射线绕点O顺时针旋转交射线于点E,连接.
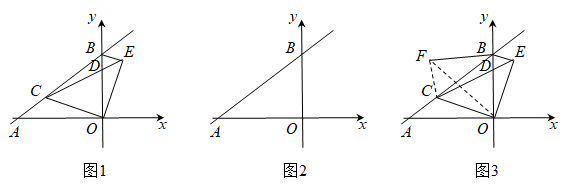 (1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)23. 给出如下规定:两个图形和 , 点P为上任一点,点Q为上任一点,如果线段的长度存在最小值,就称该最小值为两个图形和之间的距离.
(1)、证明:;(用图1)(2)、当为直角三角形时,求的长度;(用图2)(3)、点A关于射线的对称点为F,求的最小值.(用图3)23. 给出如下规定:两个图形和 , 点P为上任一点,点Q为上任一点,如果线段的长度存在最小值,就称该最小值为两个图形和之间的距离.在平面直角坐标系中,O为坐标原点.
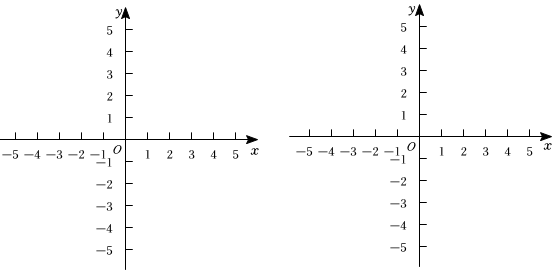 (1)、点A的坐标为 , 则点和射线之间的距离为 , 点和射线之间的距离为 .(2)、点E的坐标为 , 将射线绕原点O逆时针旋转 , 得到射线 , 在坐标平面内所有和射线之间的距离相等的点所组成的图形记为图形M.
(1)、点A的坐标为 , 则点和射线之间的距离为 , 点和射线之间的距离为 .(2)、点E的坐标为 , 将射线绕原点O逆时针旋转 , 得到射线 , 在坐标平面内所有和射线之间的距离相等的点所组成的图形记为图形M.①在坐标系中画出图形M,并描述图形M的组成部分;(若涉及平面中某个区域时可以用阴影表示)
②将抛物线与图形M的公共部分记为图形N,射线 , 组成的图形记为图形W,请直接写出图形W和图形N之间的距离.
24. 将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n]. (1)、如图①,对△ABC作变换[60°,]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;(2)、如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB′C′,使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;(3)、如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.
(1)、如图①,对△ABC作变换[60°,]得△AB′C′,则S△AB′C′:S△ABC=;直线BC与直线B′C′所夹的锐角为度;(2)、如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB′C′,使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;(3)、如图③,△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,求θ和n的值.