华师大版备考2023中考数学二轮复习 专题31 轴对称
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 如图是2022年北京冬奥运会吉祥物冰墩墩的图形,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=8;在AD上有一动点Q,则QC+QE的最小值为( )
2. 如图,在等边△ABC中,AD平分∠BAC交BC于点D,点E为AC边的中点,BC=8;在AD上有一动点Q,则QC+QE的最小值为( ) A、4 B、2 C、4 D、83. 在平面直角坐标中,点与点关于x轴对称,则点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 将一个等腰三角形纸板沿垂线段 , 进行剪切,得到三角形 , 再按如图2方式拼放,其中与共线.若 , 则的长为( )
A、4 B、2 C、4 D、83. 在平面直角坐标中,点与点关于x轴对称,则点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 将一个等腰三角形纸板沿垂线段 , 进行剪切,得到三角形 , 再按如图2方式拼放,其中与共线.若 , 则的长为( ) A、 B、 C、 D、75. 如图,将纸片沿折叠,点A落在点F处,已知 , 则的度数等于( )
A、 B、 C、 D、75. 如图,将纸片沿折叠,点A落在点F处,已知 , 则的度数等于( )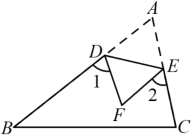 A、 B、 C、 D、6. 若点和点关于轴对称,则的值为( )A、2 B、-2 C、5 D、-57. 已知点A,B,C在上, , 把劣弧沿着直线折叠交弦于点D.若 , , 则的长为( )
A、 B、 C、 D、6. 若点和点关于轴对称,则的值为( )A、2 B、-2 C、5 D、-57. 已知点A,B,C在上, , 把劣弧沿着直线折叠交弦于点D.若 , , 则的长为( ) A、 B、9 C、 D、8. 如图,在正方形中, , 点E,F分别在边上, , 若将四边形沿折叠,点恰好落在边上,则的长度为( )
A、 B、9 C、 D、8. 如图,在正方形中, , 点E,F分别在边上, , 若将四边形沿折叠,点恰好落在边上,则的长度为( ) A、1 B、 C、 D、29. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( )
A、1 B、 C、 D、29. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( ) A、(a,a) B、 C、 D、10. 如图所示,正方形 , , 内接于五边形 , 该五边形是轴对称图形,与为对称边, , , 则的值是( )
A、(a,a) B、 C、 D、10. 如图所示,正方形 , , 内接于五边形 , 该五边形是轴对称图形,与为对称边, , , 则的值是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 点A(a,b)和B关于x轴对称,而点B与点C(2,3)关于y轴对称,那么,ab=.12. 如图,以正方形的中心为原点建立平面直角坐标系,点A的坐标为 , 则点D的坐标为 .
 13. 如图,在中, , , , 点P是线段上一动点,点M在线段上,当时,的最小值为 .
13. 如图,在中, , , , 点P是线段上一动点,点M在线段上,当时,的最小值为 . 14. 如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 .
14. 如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是 . 15. 如图,半径为6cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连结AE,BF,则图中两个阴影部分的面积为cm2
15. 如图,半径为6cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连结AE,BF,则图中两个阴影部分的面积为cm2
三、作图题
-
16. 如图,在3×6的方格纸中,已知格点P和线段AB.
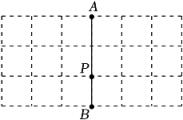
⑴画一个锐角三角形(顶点均在格点上且不与点A,B重合),使P为其中一边的中点.
⑵再画出该三角形关于直线AB对称的图形.
17. 如图,在所给网格图(每小格均为边长是1的正方形)中完成下列各题: (1)、画出格点(顶点均在格点上)关于直线对称的;(2)、在上找出点Q,使最短.
(1)、画出格点(顶点均在格点上)关于直线对称的;(2)、在上找出点Q,使最短.四、解答题
-
18. 如图所示,在矩形中, , , 若将矩形沿折叠,使点落在边上的点处,则线段的长?
 19. 如图,亮亮在A处看护羊群吃草,其家在B处,A,B到河岸的距离分别为AC=200m,BD=100m,CD=400m,亮亮从A处把羊群赶到河边饮水后回家,作图说明亮亮如何行走路程最短,并求出亮亮走的最短路程.
19. 如图,亮亮在A处看护羊群吃草,其家在B处,A,B到河岸的距离分别为AC=200m,BD=100m,CD=400m,亮亮从A处把羊群赶到河边饮水后回家,作图说明亮亮如何行走路程最短,并求出亮亮走的最短路程. 20. 如图,已知矩形ABCD,AB=4,AD=6,点E是BC的中点,将△DCE沿DE折叠得到ΔDC1E,连接BC1、CC1 , CC1与DE交于点G.求BC1的长度.
20. 如图,已知矩形ABCD,AB=4,AD=6,点E是BC的中点,将△DCE沿DE折叠得到ΔDC1E,连接BC1、CC1 , CC1与DE交于点G.求BC1的长度.
五、综合题
-
21. 如图,在平面直角坐标系中,轴,轴, , 点B的坐标为 . 将沿AC折叠得到 , 点B落在点D的位置,交y轴于点E,
 (1)、求点D的坐标.(2)、求经过点A、D的直线的解析式.22. 如图1,在长方形中, , , 动点从点出发,沿边 , 向点运动.
(1)、求点D的坐标.(2)、求经过点A、D的直线的解析式.22. 如图1,在长方形中, , , 动点从点出发,沿边 , 向点运动. (1)、当点在边上,且时,求的度数.(2)、当的面积为20时,求的长.(3)、如图2,若 , 关于直线对称.
(1)、当点在边上,且时,求的度数.(2)、当的面积为20时,求的长.(3)、如图2,若 , 关于直线对称.连结 , , 当点在边上时,求的面积.
当直线恰好经过点时,请直接写出的长度.
23. 已知中 . (1)、如图1、2,若点是上一点,且 , 点是上的动点,将沿对折,点的对应点为(点和点 在直线 的异侧),与交于点 .
(1)、如图1、2,若点是上一点,且 , 点是上的动点,将沿对折,点的对应点为(点和点 在直线 的异侧),与交于点 .①当时,求的度数.
②当是等腰三角形时,求的度数.
(2)、如图3,若点是上一点,且 , 是线段上的动点,以为直角构造等腰直角(三点顺时针方向排列),在点的运动过程中,直接写出的最小值.