华师大版备考2023中考数学二轮复习 专题29 圆的综合问题二
试卷更新日期:2023-01-06 类型:二轮复习
一、综合题
-
1. 综合与实践
 问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为 , 半径为l的扇形 , 圆锥底面是一个半径为r的圆.母线在展开图上对应的半径经过的中点.(1)、特例研究:当 , 时,n= , 展开图上,与OB的夹角为 .(2)、问题提出:求证: .(3)、问题解决:如图2,一种纸质圆锥形生日帽,底面直径为 , 母线长也为 , 为了美观,想在底面圆上一点A和与之相对的母线PB中点C之间拉一条细彩带进行装饰,求彩带长度的最小值.(提示:尝试画出圆锥侧面展开图)2. 阅读与思考
问题情境:如图,将一个圆锥的侧面展开后可得到一个圆心角为 , 半径为l的扇形 , 圆锥底面是一个半径为r的圆.母线在展开图上对应的半径经过的中点.(1)、特例研究:当 , 时,n= , 展开图上,与OB的夹角为 .(2)、问题提出:求证: .(3)、问题解决:如图2,一种纸质圆锥形生日帽,底面直径为 , 母线长也为 , 为了美观,想在底面圆上一点A和与之相对的母线PB中点C之间拉一条细彩带进行装饰,求彩带长度的最小值.(提示:尝试画出圆锥侧面展开图)2. 阅读与思考请阅读下列材料,并完成相应的任务.
在《阿基米德全集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的关于圆的一些问题,其中有这样一个问题:如图1,和是的两条弦(即折线是圆的一条折弦), , 是的中点,则从点M向所作垂线的垂足D是折弦的中点,即 . 其部分证明过程如下:

证明:如图2,在上截取 , 连接 , , 和 .
∵是的中点,
∴ ,
∵ ,
∴ ,
∴ ,
……
任务:
(1)、补全证明过程,(2)、如图3,在中, , , 若 , , , 则到的距离是 , O到的距离是 , 的半径是 . 3. 石拱桥是我国古化人民勤劳和w放的结品(如图①),隋化建造的赵州桥览今约有1400年的历史,是我国古代石拱桥的代表,如图②是根据某石供桥的实物图两出的几何图形,桥的主桥拱是圆弧形,表示为 , 桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,重足为点D,拱高(弧的中点到弦的距离)CD=5m,连接OB.
3. 石拱桥是我国古化人民勤劳和w放的结品(如图①),隋化建造的赵州桥览今约有1400年的历史,是我国古代石拱桥的代表,如图②是根据某石供桥的实物图两出的几何图形,桥的主桥拱是圆弧形,表示为 , 桥的跨度(弧所对的弦长)AB=26m,设所在圆的圆心为O,半径OC⊥AB,重足为点D,拱高(弧的中点到弦的距离)CD=5m,连接OB. (1)、直接写出AD与BD的数量关系,(2)、求这座石拱桥主桥拱的半径,(结果精确到1m)4. 如图1,已知的半径为5,弦 , 点C,D在优弧上(点B,C,D顺时针排列), , 点F是上一动点,连接并延长,交弦的延长线于点E.
(1)、直接写出AD与BD的数量关系,(2)、求这座石拱桥主桥拱的半径,(结果精确到1m)4. 如图1,已知的半径为5,弦 , 点C,D在优弧上(点B,C,D顺时针排列), , 点F是上一动点,连接并延长,交弦的延长线于点E. (1)、求证:.(2)、如图2,连接 , , .当与的某一个内角相等,且的长能确定时,求出所有满足条件的的长.(3)、如图3,当 , 时,连接 , , 交于点K,求面积与面积的比值.5. 如图,AB为的直径,点C为AB上方上一点且 , 点D为AB下方上一点,点E为AD上一点, , 连接BC,CD,BD.
(1)、求证:.(2)、如图2,连接 , , .当与的某一个内角相等,且的长能确定时,求出所有满足条件的的长.(3)、如图3,当 , 时,连接 , , 交于点K,求面积与面积的比值.5. 如图,AB为的直径,点C为AB上方上一点且 , 点D为AB下方上一点,点E为AD上一点, , 连接BC,CD,BD. (1)、求证:;(2)、求证:;(3)、连接CE,若 , , 求半径的长.6. 如图,在中, , , 对角线 , 点E在射线的延长线上,连接 , 在上取点O,以点O为圆心,长为半径作与射线切于点B,交于点F,交于点M.
(1)、求证:;(2)、求证:;(3)、连接CE,若 , , 求半径的长.6. 如图,在中, , , 对角线 , 点E在射线的延长线上,连接 , 在上取点O,以点O为圆心,长为半径作与射线切于点B,交于点F,交于点M. (1)、求证:;(2)、求的长;(3)、连接 , , 直接写出四边形的形状和面积.7. 如图,在△ABC中,AB=BC,∠ABC=90°,D是AB上一动点,连接CD,以CD为直径的⊙M交AC于点E,连接BM并延长交AC于点F,交⊙M于点G,连接BE.
(1)、求证:;(2)、求的长;(3)、连接 , , 直接写出四边形的形状和面积.7. 如图,在△ABC中,AB=BC,∠ABC=90°,D是AB上一动点,连接CD,以CD为直径的⊙M交AC于点E,连接BM并延长交AC于点F,交⊙M于点G,连接BE. (1)、求证:点B在⊙M上.(2)、当点D移动到使CD⊥BE时,求BC:BD的值.(3)、当点D到移动到使=30°时,求证:AE2+CF2=EF2 .8. 定义:△ABC中, , 则称△ABC为半余三角形,∠B叫做半余角.
(1)、求证:点B在⊙M上.(2)、当点D移动到使CD⊥BE时,求BC:BD的值.(3)、当点D到移动到使=30°时,求证:AE2+CF2=EF2 .8. 定义:△ABC中, , 则称△ABC为半余三角形,∠B叫做半余角. (1)、如图1,⊙O中,BC是直径,求证:△AOC为半余三角形.(2)、下列说法正确的是 .
(1)、如图1,⊙O中,BC是直径,求证:△AOC为半余三角形.(2)、下列说法正确的是 .①半余三角形一定是钝角三角形;
②直角三角形不可能是半余三角形;
③任何直角三角形都能分割成两个半余三角形.
(3)、如图2,⊙O中,BC是直径,AB=6,AC=8,点D是线段AC上一点(不与点A、点C重合),若△AOD为半余三角形,求OD的长.(4)、如图3,点E是直径BC上一点,△ABE为半余三角形,且∠BAE为半余角,过点E作EF⊥BC交AC于点F,若△ABC的面积为△AEF面积的7.5倍,求的值.9. 如图,在⊙O中,AB是直径,弧ACB=3弧AP,C是弧PB上一点,过点C做CD⊥AB,垂足是E,交⊙O于D,交AP的延长线于点F,连结CA,CB,PC,PD. (1)、证明:∠FPC=∠APD;(2)、若∠PAC=α,∠FPC=β,求β与α满足的关系式;(3)、连结AD,若AC=3BC,求 .10. 如图1,已知是的直径,内接于 , 点是一动点 (点不与点重合).
(1)、证明:∠FPC=∠APD;(2)、若∠PAC=α,∠FPC=β,求β与α满足的关系式;(3)、连结AD,若AC=3BC,求 .10. 如图1,已知是的直径,内接于 , 点是一动点 (点不与点重合).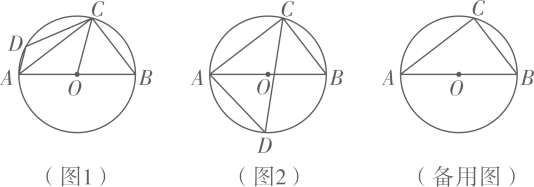 (1)、若 , 连结 , 求证: .(2)、在(1)的条件下,求的长.(3)、如图2,若平分 , 连结 , 求的面积.(4)、当为何值时,为等腰三角形?11. 如图,AB为⊙O的弦,P是优弧上的动点,PO交AB于点C,交⊙O于点D,作PF⊥AB,交OB于点E,交AB于点F,交⊙O于点G,连结CE.
(1)、若 , 连结 , 求证: .(2)、在(1)的条件下,求的长.(3)、如图2,若平分 , 连结 , 求的面积.(4)、当为何值时,为等腰三角形?11. 如图,AB为⊙O的弦,P是优弧上的动点,PO交AB于点C,交⊙O于点D,作PF⊥AB,交OB于点E,交AB于点F,交⊙O于点G,连结CE.
(1)、当∠A=∠AOC=30°时,求∠ECB的大小.(2)、当CE∥OA时,求证:== .(3)、当AC=CE,CF=FB时,求的值.12. 如图1,在平面直角坐标系中,点A(-4,0),点B是y轴正半轴上一点,以AB为直径作OM,A与C关于y轴对称,直线CM交OM于点D,E(点E在左侧),交y轴于点F.设OB=a. (1)、求M的坐标(用a的代数式表示)和AC的长.(2)、若E是半圆AB的中点,求点E的坐标.(3)、如图2,过点A作AG∥CE交y轴于点G,连结BD并延长交AG延长线于点K.
(1)、求M的坐标(用a的代数式表示)和AC的长.(2)、若E是半圆AB的中点,求点E的坐标.(3)、如图2,过点A作AG∥CE交y轴于点G,连结BD并延长交AG延长线于点K.①试说明△ABK是等腰三角形.
②当点G为AK中点时,求a的值.
13. 如图1,⊙O为锐角三角形ABC的外接圆,点D在上,AD交BC于点E,点F在AE上,满足∠AFB﹣∠BFD=∠ACB,设∠ACB=α. (1)、用含α的代数式表示∠BFD.(2)、如图2,若FG∥AC交BC于点G,BE=FG,连结BD,DG,求证:△BDE≌△FDG.(3)、在(2)的条件下,如图3,当AD为⊙O的直径,的长为2时,求的长.14. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.
(1)、用含α的代数式表示∠BFD.(2)、如图2,若FG∥AC交BC于点G,BE=FG,连结BD,DG,求证:△BDE≌△FDG.(3)、在(2)的条件下,如图3,当AD为⊙O的直径,的长为2时,求的长.14. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.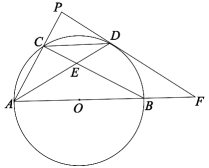 (1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.15. 一个玻璃球体近似半圆为直径,半圆上点处有个吊灯的中点为
(1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.15. 一个玻璃球体近似半圆为直径,半圆上点处有个吊灯的中点为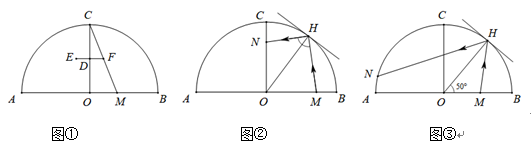 (1)、如图①,为一条拉线,在上,求的长度.(2)、如图②,一个玻璃镜与圆相切,为切点,为上一点,为入射光线,为反射光线,求的长度.(3)、如图③,是线段上的动点,为入射光线,为反射光线交圆于点在从运动到的过程中,求点的运动路径长.16. 筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹简,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线方向泻至水渠 , 水渠所在直线与水面平行;设筒车为 , 与直线交于P,Q两点,与直线交于B,C两点,恰有 , 连接 .
(1)、如图①,为一条拉线,在上,求的长度.(2)、如图②,一个玻璃镜与圆相切,为切点,为上一点,为入射光线,为反射光线,求的长度.(3)、如图③,是线段上的动点,为入射光线,为反射光线交圆于点在从运动到的过程中,求点的运动路径长.16. 筒车是我国古代利用水力驱动的灌溉工具,车轮缚以竹简,旋转时低则舀水,高则泻水.如图,水力驱动筒车按逆时针方向转动,竹筒把水引至A处,水沿射线方向泻至水渠 , 水渠所在直线与水面平行;设筒车为 , 与直线交于P,Q两点,与直线交于B,C两点,恰有 , 连接 .
 (1)、求证:为的切线;(2)、筒车的半径为 , . 当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度(精确到 , 参考值:).17. 在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“对应点”.(1)、如图,点点在线段的延长线上,若点点为点的“对应点”.
(1)、求证:为的切线;(2)、筒车的半径为 , . 当水面上升,A,O,Q三点恰好共线时,求筒车在水面下的最大深度(精确到 , 参考值:).17. 在平面直角坐标系中,已知点对于点给出如下定义:将点向右或向左平移个单位长度,再向上或向下平移个单位长度,得到点 , 点关于点的对称点为 , 称点为点的“对应点”.(1)、如图,点点在线段的延长线上,若点点为点的“对应点”.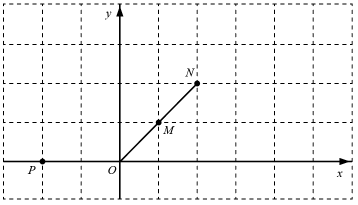
①在图中画出点;
②连接交线段于点求证:
(2)、的半径为1,是上一点,点在线段上,且 , 若为外一点,点为点的“对应点”,连接当点在上运动时直接写出长的最大值与最小值的差(用含的式子表示)18. 如图,已知是外接圆的直径, . 点D为外的一点, . 点E为中点,弦过点E. . 连接 . (1)、求证:是的切线;(2)、求证:;(3)、当时,求弦的长.19. 如图所示,在的内接中, , , 作于点P,交于另一点B,C是上的一个动点(不与A,M重合),射线交线段的延长线于点D,分别连接和 , 交于点E.
(1)、求证:是的切线;(2)、求证:;(3)、当时,求弦的长.19. 如图所示,在的内接中, , , 作于点P,交于另一点B,C是上的一个动点(不与A,M重合),射线交线段的延长线于点D,分别连接和 , 交于点E. (1)、求证: .(2)、若 , , 求的长.(3)、在点C运动过程中,当时,求的值.20. 如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H . 将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .
(1)、求证: .(2)、若 , , 求的长.(3)、在点C运动过程中,当时,求的值.20. 如图,四边形ABCD中, ,∠ABC=90°,∠C=30°,AD=3, ,DH⊥BC于点H . 将△PQM与该四边形按如图方式放在同一平面内,使点P与A重合,点B在PM上,其中∠Q=90°,∠QPM=30°, .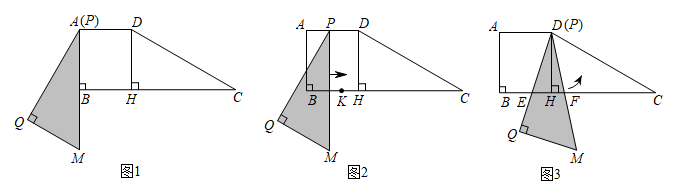 (1)、求证:△PQM≌△CHD;(2)、△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.
(1)、求证:△PQM≌△CHD;(2)、△PQM从图1的位置出发,先沿着BC方向向右平移(图2),当点P到达点D后立刻绕点D逆时针旋转(图3),当边PM旋转50°时停止.①边PQ从平移开始,到绕点D旋转结束,求边PQ扫过的面积;
②如图2,点K在BH上,且 .若△PQM右移的速度为每秒1个单位长,绕点D旋转的速度为每秒5°,求点K在△PQM区域(含边界)内的时长;
③如图3.在△PQM旋转过程中,设PQ , PM分别交BC于点E , F , 若BE=d , 直接写出CF的长(用含d的式子表示).