华师大版备考2023中考数学二轮复习 专题28 圆的综合问题一
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 如图所示,已知三角形为直角三角形,为圆切线,为切点,则和面积之比为( )
 A、 B、 C、 D、2. 如图,在矩形中, , , 为矩形内一点, , 连接 , 则的最小值为( )
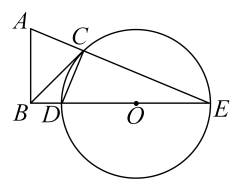
A、 B、 C、 D、2. 如图,在矩形中, , , 为矩形内一点, , 连接 , 则的最小值为( )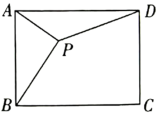 A、8 B、 C、10 D、3. 在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( )
A、8 B、 C、10 D、3. 在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,连BE,则BE的最小值为( ) A、6 B、8 C、10 D、124. 已知的直径 , 与的弦垂直,垂足为 , 且 , 则直径上的点(包含端点)与点的距离为整数的点有( )
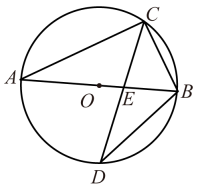
A、6 B、8 C、10 D、124. 已知的直径 , 与的弦垂直,垂足为 , 且 , 则直径上的点(包含端点)与点的距离为整数的点有( ) A、1个 B、3个 C、6个 D、7个5. 如图, 是 的直径, , 是半径 上的一动点, 交 于点 ,在半径 上取点 ,使得 , 交 于点 ,点 位于 两侧,连结 交 于点 .点 从点 出发沿 向终点 运动,在整个运动过程中, 与 的面积和的变化情况是( )
A、1个 B、3个 C、6个 D、7个5. 如图, 是 的直径, , 是半径 上的一动点, 交 于点 ,在半径 上取点 ,使得 , 交 于点 ,点 位于 两侧,连结 交 于点 .点 从点 出发沿 向终点 运动,在整个运动过程中, 与 的面积和的变化情况是( )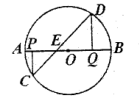 A、一直减小 B、一直不变 C、先变大后变小 D、先变小后变大6. 在平行四边形中, , , , 点E是边上的动点,过点B作直线的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( )
A、一直减小 B、一直不变 C、先变大后变小 D、先变小后变大6. 在平行四边形中, , , , 点E是边上的动点,过点B作直线的垂线,垂足为F,当点E从点A运动到点B时,点F的运动路径长为( ) A、 B、 C、 D、27. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=4.点F为射线CB上一动点,过点C作CM⊥AF于M,交AB于E,D是AB的中点,则DM长度的最小值是( )
A、 B、 C、 D、27. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=4.点F为射线CB上一动点,过点C作CM⊥AF于M,交AB于E,D是AB的中点,则DM长度的最小值是( ) A、 B、 C、 D、8. 如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )
A、 B、 C、 D、8. 如图,AB是半圆O的直径,点C在半圆O上,OA=10,BC=16,D是弧AC上一个动点,连接BD,过点C作CM⊥BD,连接AM,在点D移动的过程中,AM的最小值为( )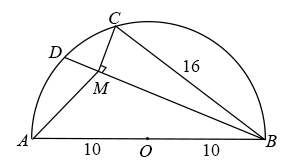 A、 B、 C、 D、9. 已知是的外接圆,半径为 , 是的高,是 的中点,与切于 , 交的延长线于 , 则下列结论:①;②EF∥BC;③;④ . 其中正确的结论是( )
A、 B、 C、 D、9. 已知是的外接圆,半径为 , 是的高,是 的中点,与切于 , 交的延长线于 , 则下列结论:①;②EF∥BC;③;④ . 其中正确的结论是( ) A、①②③ B、①③④ C、②③④ D、①②③④
A、①②③ B、①③④ C、②③④ D、①②③④二、填空题
-
10. 如图,是一条8道的跑道,每条跑道由两条直的跑道和两端是半圆形的跑道组成,每条跑道宽1米,1号跑道内侧的跑道长度为400米,则4号跑道内侧的跑道长度为米.(取3)
 11. 如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan∠CBD= , 则AD的长是 .
11. 如图,点A,C,D,B在⊙O上,AC=BC,∠ACB=90°.若CD=a,tan∠CBD= , 则AD的长是 .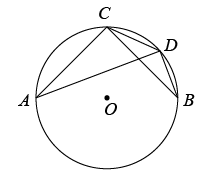 12. 如图是以点O为圆心,AB为直径的圆形纸片.点C在⊙O上,将该圆形纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E.若AD=ED,则∠B=度; 的值等于 .
12. 如图是以点O为圆心,AB为直径的圆形纸片.点C在⊙O上,将该圆形纸片沿直线CO对折,点B落在⊙O上的点D处(不与点A重合),连接CB,CD,AD.设CD与直径AB交于点E.若AD=ED,则∠B=度; 的值等于 .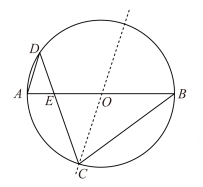 13. 如图,在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 点C是线段AO上的一个动点,连接BC,于点D,以OD为一边,作正方形ODEF,其中点E与点B在直线OD两侧,当点C从点A运动到点O过程中,点E经过的路径长为 .
13. 如图,在平面直角坐标系中,点A的坐标为 , 点B的坐标为 , 点C是线段AO上的一个动点,连接BC,于点D,以OD为一边,作正方形ODEF,其中点E与点B在直线OD两侧,当点C从点A运动到点O过程中,点E经过的路径长为 . 14. 如图,AB,CD是的弦,且 , 连接OA,OB,OC,OD,AD,BC.若 , , , 则AD的长是 .
14. 如图,AB,CD是的弦,且 , 连接OA,OB,OC,OD,AD,BC.若 , , , 则AD的长是 . 15. 如图,在矩形中, , , 点 , 分别是 , 边上的动点,且 , 点为的中点,点为上的一动点,则的最小值为 .
15. 如图,在矩形中, , , 点 , 分别是 , 边上的动点,且 , 点为的中点,点为上的一动点,则的最小值为 . 16. 如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是.
16. 如图,点P是上一点,是一条弦,点C是上一点,与点D关于对称,交于点E,与交于点F,且.给出下面四个结论:①平分; ②; ③; ④为的切线.其中所有正确结论的序号是.
三、解答题