华师大版备考2023中考数学二轮复习 专题27 有关圆的长度、面积计算
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 半径为6的圆弧的度数为 , 则它的弧长为( )A、 B、 C、 D、2. 如图,已知的半径为 , 弦直径 , , 则的长为( )
 A、 B、 C、 D、3. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )A、96πcm2 B、48πcm2 C、33πcm2 D、24πcm24. 如图,在扇形中, , 半径 , 将扇形沿过点A的直线折叠,点O恰好落在弧上的点处,折痕交于点C, 则弧的长是( )
A、 B、 C、 D、3. 已知圆锥的母线长8cm,底面圆的直径6cm,则这个圆锥的侧面积是( )A、96πcm2 B、48πcm2 C、33πcm2 D、24πcm24. 如图,在扇形中, , 半径 , 将扇形沿过点A的直线折叠,点O恰好落在弧上的点处,折痕交于点C, 则弧的长是( ) A、 B、 C、 D、5. 如图,在△ABC中,AB=AC=10,BC=12,分别以点A,B,C为圆心,AB的长为半径画弧,与该三角形的边相交,则图中阴影部分的面积为( )
A、 B、 C、 D、5. 如图,在△ABC中,AB=AC=10,BC=12,分别以点A,B,C为圆心,AB的长为半径画弧,与该三角形的边相交,则图中阴影部分的面积为( ) A、96-π B、96-25π C、48-π D、48-π6. 如图,正方形的边长为4,以为直径的半圆O交对角线于点E,则阴影部分的面积( )
A、96-π B、96-25π C、48-π D、48-π6. 如图,正方形的边长为4,以为直径的半圆O交对角线于点E,则阴影部分的面积( ) A、 B、 C、 D、7. 如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造▱ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( )
A、 B、 C、 D、7. 如图,扇形AOB圆心角为直角,OA=10,点C在上,以OA,CA为邻边构造▱ACDO,边CD交OB于点E,若OE=8,则图中两块阴影部分的面积和为( ) A、10π-8 B、5π-8 C、25π-64 D、50π-648. 如图,点A,B,C,D,E是⊙O上5个点,若AB=AO=2,将弧CD沿弦CD翻折,使其恰好经过点O,此时,图中阴影部分恰好形成一个“钻戒型”的轴对称图形,则“钻戒型”(阴影部分)的面积为( )
A、10π-8 B、5π-8 C、25π-64 D、50π-648. 如图,点A,B,C,D,E是⊙O上5个点,若AB=AO=2,将弧CD沿弦CD翻折,使其恰好经过点O,此时,图中阴影部分恰好形成一个“钻戒型”的轴对称图形,则“钻戒型”(阴影部分)的面积为( ) A、 B、4π﹣3 C、4π﹣4 D、9. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )
A、 B、4π﹣3 C、4π﹣4 D、9. 把量角器和含角的三角板按如图方式摆放:零刻度线与长直角边重合,移动量角器使外圆弧与斜边相切时,发现中心恰好在刻度处,短直角边过量角器外沿刻度处(即 , ).则阴影部分的面积为( )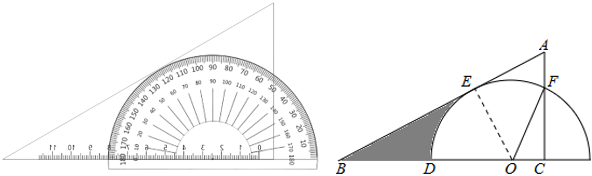 A、 B、 C、 D、10. 如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( )
A、 B、 C、 D、10. 如图,正方形的边长为6,将长为的线段的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,在上滑动,同时点F在上滑动,当点F到达点C时,运动停止,那么在这个过程中,线段的中点M所经过的路线长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
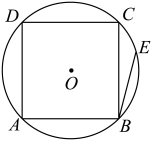
11. 已知的半径为1, , 则的长度为 .12. 如图,正方形内接于圆O,点E为上一点,连接 , 若 , , 则正方形的边长为 , 的长为 .
 13. 如图,在中, , O为边上一点,.以O为圆心,为半径作半圆与边交于E,且.若弧的长为 , 则阴影部分的面积为.
13. 如图,在中, , O为边上一点,.以O为圆心,为半径作半圆与边交于E,且.若弧的长为 , 则阴影部分的面积为. 14. 如图,图1是由若干个相同的图2组成的图案,在图2中,已知半径 , , 则图2的周长为cm(结果保留π).
14. 如图,图1是由若干个相同的图2组成的图案,在图2中,已知半径 , , 则图2的周长为cm(结果保留π). 15. 如图,正方形的边长为2,以A为圆心,长为半径画.以D为圆心,长为半径画 , 形成如图“杯子”样的阴影部分,则阴影部分的面积为.
15. 如图,正方形的边长为2,以A为圆心,长为半径画.以D为圆心,长为半径画 , 形成如图“杯子”样的阴影部分,则阴影部分的面积为. 16. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 .
16. 如图,是的外接圆,为直径,若 , , 点从点出发,在内运动且始终保持 , 当 , 两点距离最小时,动点的运动路径长为 . 17. 如图,四边形ABCD是边长为的正方形,曲线DA1B1C1D1A2 …是由多段90°的圆心角所对的弧组成的.其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1….弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A,B,C,D循环,则弧C2022D2022的长是(结果保留π).
17. 如图,四边形ABCD是边长为的正方形,曲线DA1B1C1D1A2 …是由多段90°的圆心角所对的弧组成的.其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1….弧DA1、弧A1B1、弧B1C1、弧C1D1…的圆心依次按点A,B,C,D循环,则弧C2022D2022的长是(结果保留π).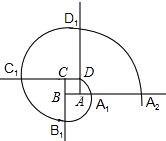
三、解答题
-
18. 如图,是以为斜边的等腰直角三角形,其内部的4段弧均等于以BC为直径的圆周,求图中阴影部分的面积.
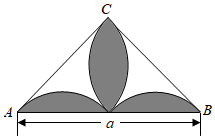 19. 如图,在△ABC中,∠ABC=90°,AB=BC=2,以点C为圆心,线段CA的长为半径作弧AD,交CB的延长线于点D,求出阴影部分的面积(结果保留π).
19. 如图,在△ABC中,∠ABC=90°,AB=BC=2,以点C为圆心,线段CA的长为半径作弧AD,交CB的延长线于点D,求出阴影部分的面积(结果保留π). 20. 如图,正三角形的边长为分别为的中点,以三点为圆心,长为半径作圆,求图中阴影部分的面积.
20. 如图,正三角形的边长为分别为的中点,以三点为圆心,长为半径作圆,求图中阴影部分的面积.
四、综合题
-
21. 如图,△ABC内接于☉O,∠A=60°,BE⊥AC于点E,延长线交☉O于点P。
 (1)、如图①,若△ABC是等边三角形,求证:OE=PE;(2)、如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,
(1)、如图①,若△ABC是等边三角形,求证:OE=PE;(2)、如图②,当点A在直线BC上方运动时,(包括点B、C)作CQ⊥AB交BE于点H,①求证:HE=PE
②若BC=3,求点H运动轨迹的长度。

