华师大版备考2023中考数学二轮复习 专题22 解直角三角形
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 某人沿坡度为的山路向上行走了30m,则该人升高了( )A、10m B、15m C、17m D、m2. 某简易房的示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AC的长为( )
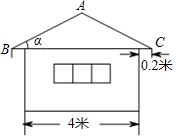 A、米 B、米 C、米 D、米3. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( )
A、米 B、米 C、米 D、米3. 如图,一条河两岸互相平行,为测得此河的宽度PT(PT与河岸PQ垂直),测P、Q两点距离为m米, , 则河宽PT的长度是( ) A、 B、 C、 D、4. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )
A、 B、 C、 D、4. 上午9时,一条船从A处出发,以每小时40海里的速度向正东方向航行,10时到达B处(如图).从A,B两处分别测得小岛M在北偏东45°和北偏东15°方向,那么船在B处时与小岛M的距离( )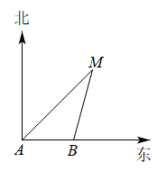 A、海里 B、海里 C、40海里 D、海里5. 如图,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上任意一点,则PK+QK的最小值为( )
A、海里 B、海里 C、40海里 D、海里5. 如图,菱形ABCD中,AB=2,∠A=120°,点P、Q、K分别为线段BC、CD、BD上任意一点,则PK+QK的最小值为( )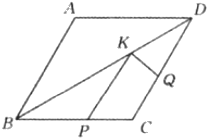 A、1 B、 C、2 D、16. 如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是( )
A、1 B、 C、2 D、16. 如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AB=8,则 BC 的长是( ) A、 B、4 C、8 D、47. 如图,在中, , 垂足为D,E为边的中点, , 则( )
A、 B、4 C、8 D、47. 如图,在中, , 垂足为D,E为边的中点, , 则( ) A、 B、 C、 D、8. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )
A、 B、 C、 D、8. 如图,某数学兴趣小组测量一棵树的高度,在点A处测得树顶C的仰角为 , 在点B处测得树顶C的仰角为 , 且A,B,D三点在同一直线上,若 , 则这棵树的高度是( )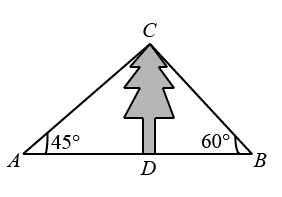 A、 B、 C、 D、9. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )
A、 B、 C、 D、9. 如图,在边长为4的正方形ABCD中,点E是CD边上的一点,点F是点D关于直线AE对称的点,连接AF、BF,若tan∠ABF=2,则DE的长是( )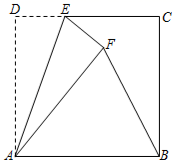 A、1 B、 C、 D、10. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( )
A、1 B、 C、 D、10. 如图,和都是等边三角形,且 , 当时,的面积为 , 则的边长为( ) A、4 B、 C、 D、
A、4 B、 C、 D、二、填空题
-
11. 中,cm,cm,则 .12. 如图是一种机器零件的示意图,其中米,米,则四边形的面积为米2
 13. 如图,在平面直角坐标系中, , 连结并延长至C,连结 , 若满足 , , 则点C的坐标为 .
13. 如图,在平面直角坐标系中, , 连结并延长至C,连结 , 若满足 , , 则点C的坐标为 .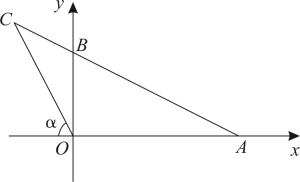 14. 一配电房示意图如图所示,它是一个轴对称图形.已知 , , 则房顶A离地面EF的高度为m.(结果精确到 , 参考数据: , , )
14. 一配电房示意图如图所示,它是一个轴对称图形.已知 , , 则房顶A离地面EF的高度为m.(结果精确到 , 参考数据: , , ) 15. 如图,已知边长为1cm的菱形AFEO,∠AFE=120°,过点O作两条夹角为60°的射线,分别交边AF,边FE于点M,N,连接MN.则下列命题:
15. 如图,已知边长为1cm的菱形AFEO,∠AFE=120°,过点O作两条夹角为60°的射线,分别交边AF,边FE于点M,N,连接MN.则下列命题:① ②MN的长度为定值 ③的形状为等边三角形 ④的最小值为3,正确的选项有(填序号)
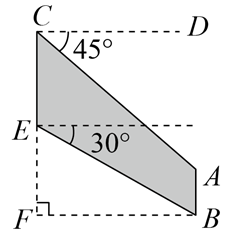
 16. 图1是一辆卸货车实物图, 折线ABC是支架, B D为可伸缩的液压支撑杆, 测得 , 图2是卸货车不工作时的侧面示意图,此时AB与FG在同一直线上,
16. 图1是一辆卸货车实物图, 折线ABC是支架, B D为可伸缩的液压支撑杆, 测得 , 图2是卸货车不工作时的侧面示意图,此时AB与FG在同一直线上,
CDll AB,且∠DEF=135°,则BF= , 图3是卸货车工作时的侧面示意图,折线CDE可绕点C上下旋转,且∠CDE始终保持不变,EF始终保持与地面垂直,当BD⊥DE时,FG与AB的距离为.


三、解答题
-
17. 如图,湖边、两点由两段笔直的观景栈道和相连.为了计算、两点之间的距离,经测量得: , , 米,求、两点之间的距离.(参考数据: , , , , , )
 18. 如图,为加快网络建设,某移动通信公司在一个坡度为2∶1的山腰上建了一座垂直于水平面的信号通信塔 , 在距山脚处水平距离39米的点处测得通信塔底处的仰角是25°,通信塔顶处的仰角是42°.请求出通信塔的大约高度(结果保留整数,参考数据: , , , ).
18. 如图,为加快网络建设,某移动通信公司在一个坡度为2∶1的山腰上建了一座垂直于水平面的信号通信塔 , 在距山脚处水平距离39米的点处测得通信塔底处的仰角是25°,通信塔顶处的仰角是42°.请求出通信塔的大约高度(结果保留整数,参考数据: , , , ).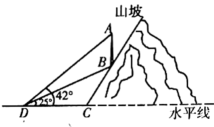 19. 如图,在Rt中,∠ACB=90°,CD、CH分别是AB边上的中线和高, , , 求AB、CH的长.
19. 如图,在Rt中,∠ACB=90°,CD、CH分别是AB边上的中线和高, , , 求AB、CH的长. 20. 如图,在△ABC中,∠C = 90°, , D为AC上一点,∠BDC = 45°,CD=6.求AD的长.
20. 如图,在△ABC中,∠C = 90°, , D为AC上一点,∠BDC = 45°,CD=6.求AD的长.
四、综合题
-
21. 如图,抛物线
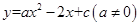 与
与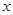 轴交于A、B(3,0)两点,与
轴交于A、B(3,0)两点,与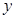 轴交于点C(0,-3),抛物线的顶点为D.
轴交于点C(0,-3),抛物线的顶点为D.
 (1)、求抛物线的解析式;(2)、已知点M是x轴上的动点,过点M作x轴的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.(3)、在直线BC下方抛物线上一点P,作PQ垂直BC于点Q,连接CP,当△CPQ中有一个角等于∠ACO时,求点P的坐标。
(1)、求抛物线的解析式;(2)、已知点M是x轴上的动点,过点M作x轴的垂线交抛物线于点G,是否存在这样的点M,使得以点A、M、G为顶点的三角形与△BCD相似,若存在,请求出点M的坐标;若不存在,请说明理由.(3)、在直线BC下方抛物线上一点P,作PQ垂直BC于点Q,连接CP,当△CPQ中有一个角等于∠ACO时,求点P的坐标。

