华师大版备考2023中考数学二轮复习 专题21 相似三角形
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 若两个相似三角形的对应边之比为 , 则这两个相似三角形的周长之比为( )A、 B、 C、 D、2. 如图,ΔABC中,DE∥BC,且AD:DB=1:2.则ΔADE与ΔABC的面积比是( )
 A、 B、 C、 D、3. 如图,在Rt△ABC中,CD是斜边AB上的高,则下列结论正确的是( )
A、 B、 C、 D、3. 如图,在Rt△ABC中,CD是斜边AB上的高,则下列结论正确的是( ) A、BD=AD B、BC2=AB•CD C、AD2=BD•AB D、CD2=AD•BD4. 下列各组条件中一定能推得△ABC与△DEF相似的是( )A、 B、 , 且∠A=∠E C、 , 且∠A=∠D D、且∠A=∠D5. 如图,在中, , 将绕点C顺时针旋转得到 , 使点B的对应点E恰好落在边上,点A的对应点为D,延长交于点F,则下列结论一定正确的是( )
A、BD=AD B、BC2=AB•CD C、AD2=BD•AB D、CD2=AD•BD4. 下列各组条件中一定能推得△ABC与△DEF相似的是( )A、 B、 , 且∠A=∠E C、 , 且∠A=∠D D、且∠A=∠D5. 如图,在中, , 将绕点C顺时针旋转得到 , 使点B的对应点E恰好落在边上,点A的对应点为D,延长交于点F,则下列结论一定正确的是( ) A、 B、 C、 D、6. 如图,已知与相交于点 , , 那么下列式子中错误的是( )
A、 B、 C、 D、6. 如图,已知与相交于点 , , 那么下列式子中错误的是( )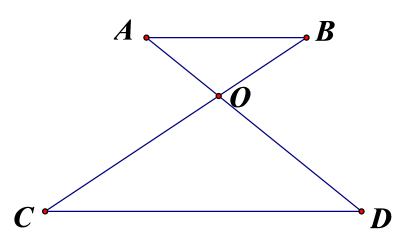 A、 B、 C、 D、7. 如图,在Rt△ABC中,∠C=90°,放置边长分别为3,4,x的三个正方形,则x的值为( )
A、 B、 C、 D、7. 如图,在Rt△ABC中,∠C=90°,放置边长分别为3,4,x的三个正方形,则x的值为( ) A、12 B、7 C、6 D、58. 如图,中, , 点D是上一动点,连接 , 将线段绕点C逆时针旋转90°得到线段 , 连接 , 当面积最大时,的长为( )
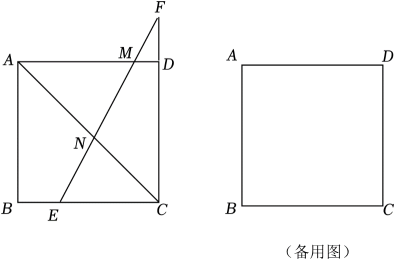
A、12 B、7 C、6 D、58. 如图,中, , 点D是上一动点,连接 , 将线段绕点C逆时针旋转90°得到线段 , 连接 , 当面积最大时,的长为( ) A、2 B、 C、 D、9. 如图,四边形ABCD中,对角线AC,BD交于点E. 若 , 则下列结论中正确的是( )
A、2 B、 C、 D、9. 如图,四边形ABCD中,对角线AC,BD交于点E. 若 , 则下列结论中正确的是( )
①
②与的周长比为③
④S△ABE·S△DCE=S△ADE·S△BCEA、③④ B、①②③ C、①②④ D、①②③④二、填空题
-
10. 若两个相似三角形的周长比是4:9,则对应角平分线的比是 .11. 如图,在中,D是AB的中点,过点D的直线交AC于E,交BC的延长线于F,当 , 时, .
 12. 已知 , 顶点、、分别与、、对应, , 、分别是边、的中点,如果 , 那么的长为 .13. 如图,D、E是边、上的两点,且 , , 那么 .
12. 已知 , 顶点、、分别与、、对应, , 、分别是边、的中点,如果 , 那么的长为 .13. 如图,D、E是边、上的两点,且 , , 那么 . 14. 已知与相似,且点A与点是对应点,点与点是对应点,如果 , , 那么 .15. 如图,在 , 平分 , , , , , 则 .
14. 已知与相似,且点A与点是对应点,点与点是对应点,如果 , , 那么 .15. 如图,在 , 平分 , , , , , 则 . 16. 如图是护眼学习台灯,该台灯的活动示意图如图所示灯柱 , 灯臂绕着支点C可以旋转,灯罩呈圆弧形(即和)在转动过程中,总是与桌面平行当时, , , 测得点M在墙壁上,且;当灯臂转到位置时,测得 , 则点E到桌面的距离为 若此时点C,F,M在同一条直线上,的最低点到桌面的距离为 , 则所在圆的半径为 .
16. 如图是护眼学习台灯,该台灯的活动示意图如图所示灯柱 , 灯臂绕着支点C可以旋转,灯罩呈圆弧形(即和)在转动过程中,总是与桌面平行当时, , , 测得点M在墙壁上,且;当灯臂转到位置时,测得 , 则点E到桌面的距离为 若此时点C,F,M在同一条直线上,的最低点到桌面的距离为 , 则所在圆的半径为 .
三、作图题
-
17. 如图,在7×4方格纸中,点A,B,C都在格点上(△ABC称为格点三角形,即格点△ABC),用无刻度直尺作图.
 (1)、在图1中的线段AC上找一个点D,使CD=AC;(2)、在图2中作一个格点△CEF,使△CEF与△ABC相似.
(1)、在图1中的线段AC上找一个点D,使CD=AC;(2)、在图2中作一个格点△CEF,使△CEF与△ABC相似.四、解答题
-
18. 如图,在矩形中,点E,F分别在边 , 上, , , , , , 求的长.

五、综合题
-