2022-2023学年浙教版数学七年级下册2.4二元一次方程组的应用同步练习

试卷更新日期：2023-01-06 类型：同步测试

进入出卷网下载

一、单选题

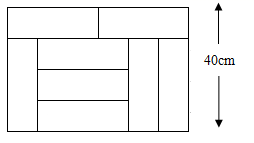
1. 某玩具厂共有300名生产工人，每个工人每天可生产玩具车架20个或车轮40个，且1个车架与4个车轮可配成一套，设有x个工人生产车架，y个工人生产车轮，下列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 300 \\ 40 x = 20 y \end{array}$ B、 ${\begin{array}{l} x + y = 300 \\ 20 x = 40 y \end{array}$ C、 ${\begin{array}{l} x + y = 300 \\ 4 \times 20 x = 40 y \end{array}$ D、 ${\begin{array}{l} x + y = 300 \\ 20 x = 4 \times 40 y \end{array}$

查看试题解析
2. 顺风旅行社组织200人到花果岭和云水涧旅游，到花果岭的人数比到云水涧的人数的2倍少1人．设到花果岭的人数为x人，到云水涧的人数为y人，根据题意可列方程组为（）

A、 ${\begin{matrix} x + y = 200 \\ x = 2 y - 1 \end{matrix}$ B、 ${\begin{matrix} x + y = 200 \\ y = 2 x - 1 \end{matrix}$ C、 ${\begin{matrix} x + y = 200 \\ x = 2 y + 1 \end{matrix}$ D、 ${\begin{matrix} x + y = 200 \\ y = 2 x + 1 \end{matrix}$

查看试题解析
3. 有48支队伍520名运动员参加篮球、排球比赛，其中每支篮球队10人，每支排球队12人，每名运动员只能参加一项比赛，则排球队有多少支队伍参赛？（）

A、28 B、20 C、32 D、26

查看试题解析
4. 如图，宽为40cm的长方形图案由10个相同的小长方形拼成，其中一个小长方形的面积为（）

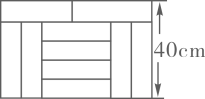A、256cm² B、320cm² C、360cm² D、400cm²

查看试题解析
5. 已知关于x、y的二元一次方程组 ${\begin{cases} x + 3 y = 4 - a ， \\ x - y = 3 a \end{cases}$ 其中 $- 3 \leq a \leq 1$ ，给出下列四个结论：①当 $a = 0$ 时，方程组的解也是方程 $x + y = 2 - a$ 的解；②当 $a = - 2$ 时，x、y的值互为相反数；③若 $x \leq 1$ ，则 $1 \leq y \leq 4$ ；④ ${\begin{array}{l} x = 4 ， \\ y = - 3 \end{array}$ 是方程组的解．其中正确的结论有（）个．

A、1 B、2 C、3 D、4

查看试题解析
6. 在等式 $y = k x + b$ 中，当x=0时，y= $- 1$ ；当x= $- 1$ 时，y=0，则这个等式是（）

A、 $y = - x - 1$ B、 $y = - x$ C、 $y = - x + 1$ D、 $y = x + 1$

查看试题解析
7. 小虎、大壮和明明三人玩飞镖游戏，各投5支镖，规定在同一环内得分相同，中靶和得分情况如图，则大壮的得分是（）

A、20 B、22 C、23 D、25

查看试题解析
8. 为了鼓励市民节约用电，某市对居民用电实行“阶梯收费”（总电费=第一阶梯电费+第二阶梯电费）.规定：每月用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费. 如图是张磊家2021年9月和10月所交电费的收据，则该市规定的第一阶梯电价和第二阶梯电价分别为每度（）
代收电费收据

2021年9月

电表号

1205

户名

张磊

月份

9月

用电量

220度

金额

112元

代收电费收据

2021年10月

电表号

1205

户名

张磊

月份

10月

用电量

265度

金额

139元

A、0.5元，0.6元 B、0.4元，0.5元 C、0.3元，0.4元 D、0.6元，0.7元

查看试题解析
9. 一食品原料厂某日用大小两种货车运货两次.第一次用2辆大货车和6辆小货车运货23吨；第二次用5辆大货车和6辆小货车运货35吨.小明比较这两次运货，知道3辆大货车一次可运货12吨.若设1辆大货车和1辆小货车一次分别运货x吨和y吨，根据该日两次运货的信息，可列方程组 ${\begin{matrix} 2 x + 6 y = 23 ① \\ 5 x + 6 y = 35 ② \end{matrix}$ .若对该方程组进行变形，下列变形中可直接得到小明所说的“3辆大货车一次可运货12吨”的是（）

A、①+② B、②﹣① C、②﹣①×2 D、①×5﹣②×2

查看试题解析
10. 在《九章算术》中，一次方程组是由算筹布置而成的．如图1所示的算筹图，表示的方程组就是 ${\begin{cases} 2 x + y = 11 ， \\ 4 x + 3 y = 27 ， \end{cases}$ 类似地，图2所示的算筹图表示的方程组为（）

A、 ${\begin{cases} 3 x + 2 y = - 14 ， \\ x + 4 y = 23 \end{cases}$ B、 ${\begin{cases} 3 x + 2 y = - 9 ， \\ x + 4 y = 23 \end{cases}$ C、 ${\begin{cases} 3 x + 2 y = 19 ， \\ x + 4 y = 3 \end{cases}$ D、 ${\begin{cases} 3 x + 2 y = 19 ， \\ x + 4 y = 23 \end{cases}$

查看试题解析

二、填空题

11. 小明家准备装修一套新房，若甲、乙两家装修公司合作需6周完成，装修费用为5.2万元；若甲公司单独做4周，剩下的由乙公司做，还需9周完成，此时装修费用为4.8万元.若小明只选甲公司单独完成，则他需要付给甲公司装修费用万元.

查看试题解析
12. 某果园计划种植梨树和苹果树共1000株，实际上梨树种植量比计划增长10%，而苹果树种植量比计划减少5%.若设实际种植梨树x株，苹果树y株，列二元一次方程为.

查看试题解析
13. 小明在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形（如图甲）；小红看见了，说：“我也来试一试，”结果小红七拼八凑，拼成了如图乙那样的正方形，中间还留下了一个洞，恰好是边长为 $3 mm$ 的小正方形，则每个小长方形的面积为 ${mm}^{2}$ .

查看试题解析
14. 问题解决：糖葫芦一般是用竹签串上山楂．再蘸以冰糖制作而成，现将一些山楂分别串在若干个竹签上，如果每根竹签串4个山楂，还剩余3个山楂；如果每根竹签串7个山楂，还剩余6根竹签，求竹签有多少根？山楂有多少个？反思归纳：现有m根竹签，n个山楂，若每根竹签串a个山楂，还剩b个山楂，则m、n、a、b满足的等量关系为（用含m、n、a、b的代数式表示）．

查看试题解析
15. 定义一种新的运算：a☆b=2a-b，例如：3☆（-1）=2×3-（-1）=7。若a☆b=0，且关于x，y的二元一次方程（a+1）x-by-a+3=0，当a，b取不同值时，方程都有一个公共解，那么这个公共解为

查看试题解析
16. 一家商店进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付两组费用共3520元，若先请甲组单独做6天，再请乙组单独做12天可以完成，需付费用3480元，问：甲、乙两组工作一天，商店各应付多少钱？设：甲组工作一天商店应付x元，乙组工作一天商店付y元．列二元一次方程组为．

查看试题解析

三、计算题

17. 已知方程组 ${\begin{matrix} a x + y = 15 ， (1) \\ 4 x - b y = - 2. (2) \end{matrix}$ 甲由于看错了方程（1）中的a，得到方程组的解为 ${\begin{matrix} x = - 3 \\ y = - 1 \end{matrix}$ ，乙由于看错了方程(2)中的b，得到方程组的解为 ${\begin{matrix} x = 4 ， \\ y = 3. \end{matrix}$ ，若按正确的计算，求x＋6y的值.

查看试题解析

四、解答题

18. 2022年冬奥会上智慧化全覆盖，机器人得到广泛应用，冬奥会组委会针对不同的物品运送场景选取了几个不同类型的智能物流机器人．这样不仅能高效运输，同时也能减少人员接触．具体运输情况如下表所示：

	A型机器人/个	B型机器人/个	运输物品总数/件
第一批	2	5	34
第二批	4	3	26

问：每个 $A$ 型机器人和 $B$ 型机器人分别可以运输物品多少件？

查看试题解析

19. 小明和小丽两人相距8千米，小明骑自行车，小丽步行．两人同时出发相向而行，0.8小时相遇：若两人同时出发同向而行，小明2小时可以追上小丽，求小明、小丽每小时各前行多少千米？

查看试题解析
20. 某车间有14名工人生产一种螺栓和螺母，每人每天平均能生产螺栓6个或螺母9个，要求1个螺栓配2个螺母，应怎样分配工人才能使每天生产的螺栓和螺母恰好配套？

查看试题解析
21. 某同学用8块相同的长方形地砖拼成一个矩形，如图所示，求每块地砖的面积是多少？

查看试题解析

电表号	1205
户名	张磊
月份	9月
用电量	220度
金额	112元

2022-2023学年浙教版数学七年级下册2.4二元一次方程组的应用 同步练习

一、单选题

二、填空题

三、计算题

四、解答题

2022-2023学年浙教版数学七年级下册2.4二元一次方程组的应用同步练习