山西省忻州市代县2022-2023学年八年级上学期期末考试数学试卷

试卷更新日期：2023-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 $a^{2} \cdot a^{3}$ 的结果是（　　）

A、 $a^{2}$ B、 $a^{3}$ C、 $a^{5}$ D、 $a^{6}$

查看试题解析
2. 为了直观地表示世界七大洲的面积各占全球陆地面积的百分比，最适合使用的统计图是（）

A、扇形统计图 B、条形统计图 C、折线统计图 D、以上都可以

查看试题解析
3. 已知一组数据： $π$ ， $- \frac{2}{3}$ ， 0.1010010001， $- \frac{\sqrt{3}}{2}$ ， $0 . \dot{2}$ ，其中无理数出现的频数是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 下列各式中，能用平方差公式分解因式的是（）

A、 $x^{2} - x$ B、 $x^{2} + 2 x - 1$ C、 $x^{2} + y^{2}$ D、 $x^{2} - 1$

查看试题解析
5. 在 $△ A B C$ 中，若 $A C^{2} - B C^{2} = A B^{2}$ ，则（）

A、 $∠ A = 90 °$ B、 $∠ B = 90 °$ C、 $∠ C = 90 °$ D、不能确定

查看试题解析
6. 在测量一个小口圆形容器的内径时，小明用“X型转动钳”按如图所示的方法进行测量，其中 $O A = O D ， O B = O C$ ，因此可得 $△ A O B ≌ △ D O C$ ，从而测得 $A B$ 的长，就可以得到圆形容器的内径 $C D$ 的长，其中判定 $△ A O B ≌ △ D O C$ 的依据是（）

A、 $S A S$ B、 $H L$ C、 $A S A$ D、 $S S S$

查看试题解析
7. 估计 $\sqrt[3]{30}$ 的值（）

A、在6和7之间 B、在5和6之间 C、在4和5之间 D、在3和4之间

查看试题解析
8. 关于原命题“如果 $a = b$ ，那么 $a^{2} = b^{2}$ ”和它的逆命题“如果 $a^{2} = b^{2}$ ，那么 $a = b$ ”，下列说法正确的是（）

A、原命题是真命题，逆命题是假命题 B、原命题、逆命题都是真命题 C、原命题是假命题，逆命题是真命题 D、原命题，逆命题都是假命题

查看试题解析
9. 如图，在 $△ A B C$ 中， $∠ B = 54 °$ ，以点C为圆心， $C A$ 的长为半径作弧交 $A B$ 于点D，分别以点A和点D为圆心，大于 $A D$ 的长为半径作弧，两弧相交于点E，作直线 $C E$ ，交 $A B$ 于点F，则 $∠ B C F$ 的度数是（）

A、54° B、36° C、27° D、18°

查看试题解析
10. 公元前500年，毕达哥拉斯学派中的一名成员西伯索斯发现了无理数，导致了第一次数学危机．事实上，我国古代发现并阐述无理数的概念比西方更早，但是没有系统的理论．《九章算术》的开方术中指出了存在有开不尽的情形：“若开方不尽者，为不可开．”《九章算术》的作者们给这种“不尽根数”起了一个专门名词—“面”“面”就是无理数．无理数中最具有代表性的数就是“ $\sqrt{2}$ ”．下列关于 $\sqrt{2}$ 的说法错误的是（）

A、可以在数轴上找到唯一一点与之对应 B、它是面积为2的正方形的边长 C、可以用两个整数的比表示 D、可以用反证法证明它不是有理数

查看试题解析

二、填空题

11. 计算： $\sqrt[3]{- 8}$ = ．

查看试题解析
12. 用反证法证明，“在△ABC中，∠A、∠B对边是a、b，若∠A＞∠B，则a＞b．”第一步应假设．

查看试题解析
13. 实行“双减”政策后，某区推行“5+2”的课后服务模式，学校科学利用课余时间，开展丰富的社团活动．下表是根据某学校八（1）班同学参加课外社团活动情况收集到的数据绘制的部分统计表，若选择足球的人数占该班总人数的25%，则选择手工的人数为．
八（1）班同学参加社团活动情况统计表
社团活动
足球
啦啦操
合唱
手工
其他
参加人数
10
16
4

2

查看试题解析
14. 如图，小虎用10块高度都是 $3 c m$ 的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（ $A C = B C$ ， $∠ A C B = 90 °$ ），点C在 $D E$ 上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离为．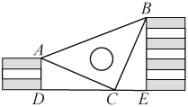

查看试题解析
15. 如图，在Rt△ACB中，∠ACB＝90°，BC＝6，AC＝9.折叠△ACB，使点A与BC的中点D重合，折痕交AB于E，交AC于点F，则CF＝.

查看试题解析

三、解答题

16.

(1)、计算： ${(- 2 m)}^{2} \div 2 m^{2}$ ．

(2)、先化简，再求值 $(1 + a) (1 - a) + {(a - 2)}^{2}$ ，其中 $a = - 2$ ．

查看试题解析
17. 如图，已知 $△ A B C$ ．

(1)、利用直尺和圆规，根据下列要求作图．（保留作图痕迹，不要求写作法）
①作 $∠ A B C$ 的平分线 $B D$ 交 $A C$ 于点D；
②作线段 $B D$ 的垂直平分线交 $A B$ 于点E，交 $B C$ 于点F，交 $B D$ 于点M．

(2)、试判断 $△ B E F$ 的形状，并加以证明．

查看试题解析
18. 如图， $△ A B C$ 是张大爷的一块小菜地，已知CD是 $△ A B C$ 中AB边上的高， $A C = 5 ， C D = 4 ， B C = 3 A D$ ，求BD的长．（结果保留根号）

查看试题解析
19. 2022年北京冬奥会捷报传来——中国队9金4银2铜收官，这极大地激励了同学们体育锻炼的热情．某校体育部随机抽查八年级（1）班学生一周内平均每天的体育锻炼时间t（单位：分钟），并将调查的数据整理后得到如下统计图表：
组别
锻炼时间
频数
Ａ
$0 \leq t < 20$
4
Ｂ
$20 \leq t < 30$
8
Ｃ
$30 \leq t < 40$
10
Ｄ
$40 \leq t < 50$
a
Ｅ
$t \geq 50$
b
根据图表中提供的信息，解答下列问题．

(1)、统计表中的a= ， b= ，并补全条形统计图．

(2)、求扇形统计图中，C组所在扇形圆心角的度数．

(3)、根据抽样调查结果，求出锻炼时间不低于30分钟的有多少名学生?

查看试题解析
20. 阅读与思考
我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式，如果一个多项式不是完全平方式，我们常常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决数学问题的方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决与非负数有关的问题和求代数式最大值，最小值等问题．
例如： $x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = {(x + 1)}^{2} - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$ ；
$x^{2} + 2 x + 6 = x^{2} + 2 x + 1 + 5 = {(x + 1)}^{2} + 5$ ，则当 $x = - 1$ 时， $x^{2} + 2 x + 6$ 有最小值，最小值是5．
根据材料用配方法解决下列问题．

(1)、若多项式 $x^{2} + 6 x + k$ 是一个完全平方式，则常数k的值为____．

A、9 B、-9 　　　 C、±9 D、36

(2)、分解因式： $x^{2} - 2 x - 8$ ．

(3)、当x为何值时，多项式 $x^{2} - 4 x + 3$ 有最小值?并求出这个最小值．

查看试题解析
21. 如图，在△ABC中，AB＝AC ，点D、E、F分别在AB、BC、AC边上，且BE＝CF ， BD＝CE ．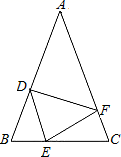

(1)、求证：△DEF是等腰三角形；

(2)、当∠A＝40°时，求∠DEF的度数．

查看试题解析
22. 综合与实践
美丽的弦图中蕴含着四个全等的直角三角形．

(1)、如图1，弦图中包含了一大一小两个正方形，已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c，结合图1，试验证勾股定理；

(2)、如图2，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓（实线）的周长为24， $O C = 3$ ，求该飞镖状图案的面积；

(3)、如图3，将八个全等的直角三角形紧密地拼接，记图中正方形 $A B C D$ ，正方形 $E F G H$ ，正方形 $M N K T$ 的面积分别为 $S_{1} ， S_{2} ， S_{3}$ ，若 $S_{1} + S_{2} + S_{3} = 42$ ，求 $S_{2}$ 的值．

查看试题解析
23. 综合与探究
已知在 $R t △ A B C$ 中， $A B = A C ， ∠ B A C = 90 °$ ， D为直线 $B C$ 上一动点（点D不与点B，点C重合），以 $A D$ 为边作 $R t △ A D E$ （其中 $A D = A E ， ∠ D A E = 90 °$ ），连接 $C E$ ．

(1)、如图1，当点D在边 $B C$ 上时，求 $∠ D C E$ 的度数．

(2)、如图2，当点D在边 $B C$ 的延长线上运动时，类比第（1）问，请你猜想线段 $B D$ ， $C D$ ， $D E$ 的数量关系，并说明理由．

(3)、如图3，当点D在边 $C B$ 的延长线上时， $A C = \sqrt{2} ， C E = 1$ ，求线段 $D E$ 的长．

查看试题解析

社团活动	足球	啦啦操	合唱	手工	其他
参加人数	10	16	4		2

组别	锻炼时间	频数
Ａ	$0 \leq t < 20$	4
Ｂ	$20 \leq t < 30$	8
Ｃ	$30 \leq t < 40$	10
Ｄ	$40 \leq t < 50$	a
Ｅ	$t \geq 50$	b