山东省烟台市龙口市2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列分式中，是最简分式的是（）

A、 $\frac{6 x}{4 y}$ B、 $\frac{x^{2} + y^{2}}{x - y}$ C、 $\frac{1 - x}{x - 1}$ D、 $\frac{x y + x^{2}}{x}$

查看试题解析
2. 七巧板是我国的一种传统智力玩具，下列用七巧板拼成的图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 在 $▱ A B C D$ 中，若 $∠ A + ∠ C = 80 °$ ，则 $∠ B$ 的度数是（）

A、140° B、120° C、100° D、40°

查看试题解析
4. 如图，菱形 $A B C D$ 的对角线AC与BD相交于点O，若 $A B = 5$ ， $A C = 6$ ，则 $B D$ 的长为（）

A、4 B、6 C、7 D、8

查看试题解析
5. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，某校调查了一个班50名学生每天的睡眠时间，绘成睡眠时间条形统计图如图所示，则所调查学生睡眠时间的中位数为（）

A、6h B、7h C、7.5h D、8h

查看试题解析
6. 如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为 $α$ ， $β$ ，则正确的是（）

A、 $α - β = 0$ B、 $α - β < 0$ C、 $α - β > 0$ D、无法比较 $α$ 与 $β$ 的大小

查看试题解析
7. 如图所示的扇形统计图描述了某校学生对课后延时服务的打分情况（满分5分），则所打分数的众数为（）

A、5分 B、4分 C、3分 D、45%

查看试题解析
8. 当m为自然数时， $(4 m + 5)^{2} - 9$ 一定能被下列哪个数整除（）

A、 $5$ B、 $6$ C、 $7$ D、 $8$

查看试题解析
9. 如图，四边形ABCD是正方形，△ADE绕着点A旋转90°后到达△ABF的位置，连接EF，则△AEF的形状是（）

A、等腰三角形 B、直角三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
10. 如图，等腰直角三角形 $A B C$ 中， $∠ A B C = 90 °$ ， $B A = B C$ ，将 $B C$ 绕点B顺时针旋转（ $0 ° < θ < 90 °$ ），得到 $B P$ ，连接 $C P$ ，过点A作 $A H ⊥ C P$ 交 $C P$ 的延长线于点H，连接 $A P$ ，则 $∠ P A H$ 的度数（　　）

A、随着 $θ$ 的增大而增大 B、随着 $θ$ 的增大而减小 C、保持定值 $45 °$ 不变 D、随着 $θ$ 的增大，先增大后减小

查看试题解析

二、填空题

11. 如果关于x的方程 $\frac{2}{x - 3} = 1 - \frac{m}{x - 3}$ 有增根，那么m的值为．

查看试题解析
12. 已知关于x的二次三项式 $x^{2} + k x + 9$ 是完全平方式，则常数k的值为．

查看试题解析
13. 已知一组数据x₁ ， x₂ ， x₃的平均数和方差分别为5和2，则数据x₁+1，x₂+1，x₃+1的平均数是，标准差是．

查看试题解析
14. 如图，在平行四边形ABCD中，AD=5，AB=3，AE平分∠BAD交BC边于点E，则EC的长为．

查看试题解析
15. 如图，将长5cm，宽3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为 cm² ．

查看试题解析
16. 如图，在平面直角坐标系中，平行四边形ABCD三个顶点坐标分别为A(-1，-2) ， D(1，1) ，C(5，2) ，则顶点B的坐标为

查看试题解析

三、解答题

17. 分解因式：

(1)、 $a^{2} (x - y) - 4 (y - x)$ ；

(2)、 $4 (x + 2) (x - 3) + 25$ ．

查看试题解析
18. 解方程： $\frac{1}{x} - \frac{2}{x^{2} - 2 x} = \frac{3}{x - 2}$ ．

查看试题解析
19. 先化简 $(\frac{3}{a + 1} - a + 1) \div \frac{a^{2} - 4 a + 4}{a + 1}$ ，然后从 $- 2 \leq a \leq 2$ 的范围内选择一个合适的整数作为a的值代入求值．

查看试题解析
20. 如图，已知△ABC的三个顶点的坐标分别为 $A (- 5 ， 0)$ 、 $B (- 2 ， 3)$ 、 $C (- 1 ， 0)$ ．

(1)、画出 $△ A B C$ 关于原点O成中心对称的图形 $△ A^{'} B^{'} C^{'}$ ；

(2)、将 $△ A B C$ 绕原点O顺时针旋转 $90 °$ ，画出对应的 $△ A^{″} B^{″} C^{″}$ ，并写出点 $B^{″}$ 的坐标．

查看试题解析
21. 核酸检测时采集的样本必须在4小时内送达检测中心，超过时间，样本就会失效.A、B两个采样点到检测中心的路程分别为30千米、36千米.A、B两个采样点的送检车有如下信息：
信息一：B采样点送检车的平均速度是A采样点送检车的1.2倍；

信息二：A、B两个采样点送检车行驶的时间之和为2小时.

若B采样点从开始采集样本到送检车出发用了2.6小时，则B采样点采集的样本会不会失效？

查看试题解析
22. 在学校组织的“文明出行”知识竞赛中，8（1）和8（2）班参赛人数相同，成绩分为A、B、C三个等级，其中相应等级的得分依次记为A级100分、B级90分、C级80分，其中8（2）班有2人达到A级，将两个班的成绩整理并绘制成如下的统计图．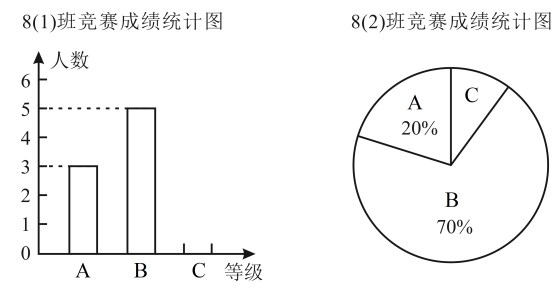
请解答下列问题：

(1)、求各班参赛人数，并补全条形统计图；

(2)、此次竞赛中8（2）班成绩的中位数a为分；

(3)、小明同学根据以上信息制作了如下统计表：

平均数（分）
中位数（分）
方差
8（1）班
m
90
n
8（2）班
91
a
29
请分别求出m和n的值，并从稳定性方面比较两个班的成绩．

查看试题解析
23. 如图，在矩形 $A B C D$ 中，对角线 $A C ， B D$ 相交于点O， $∠ A D F ： ∠ F D C = 3 ： 2$ ， $D F ⊥ A C$ 交 $B C$ 于F，垂足为E，求 $∠ B D F$ 的度数．

查看试题解析
24. 如图，在 $▱ A B C D$ 中， $∠ C = 60 °$ ， M、N分别是 $A D 、 B C$ 的中点．

(1)、求证：四边形 $M N C D$ 是平行四边形；

(2)、若 $B C = 2 C D$ ， $M N = 1$ ，求 $B D$ 的长．

查看试题解析
25. 如图①，△ABC中，AB=AC，点M、N分别是AB、AC上的点，且AM=AN．连接MN、CM、BN，点D、E、F、G分别是BC、MN、BN、CM的中点，连接E、F、D、G．

(1)、判断四边形EFDG的形状是（不必证明）；

(2)、现将△AMN绕点A旋转一定的角度，其他条件不变（如图②），四边形EFDG的形状是否发生变化？证明你的结论；

(3)、如图②，在（2）的情况下，请将△ABC在原有的条件下添加一个条件，使四边形EFDG是正方形．请写出你添加的条件，并在添加条件的基础上证明四边形EFDG是正方形．

查看试题解析

	平均数（分）	中位数（分）	方差
8（1）班	m	90	n
8（2）班	91	a	29