山东省烟台市莱州市2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-01-06 类型:期末考试
一、单选题
-
1. 本学期我们学习了三种几何变换:平移、轴对称、旋转,下列著名商标设计中,有三个都可以由基础图形平移得到,则不能由基础图形通过平移变换而得到的商标是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列多项式,能用平方差公式分解的是( )A、 B、 C、 D、3. 若一个正n边形的每个内角为144°,则这个正n边形的边数是( )A、5 B、8 C、10 D、124. 下列说法正确的是( )A、代数式是分式 B、分式中x,y都扩大2倍,分式的值不变 C、分式的值为0,则x的值为-2 D、分式是最简分式5. 如图,四边形的对角线交于点O,下列哪组条件能判断四边形是平行四边形( )
2. 下列多项式,能用平方差公式分解的是( )A、 B、 C、 D、3. 若一个正n边形的每个内角为144°,则这个正n边形的边数是( )A、5 B、8 C、10 D、124. 下列说法正确的是( )A、代数式是分式 B、分式中x,y都扩大2倍,分式的值不变 C、分式的值为0,则x的值为-2 D、分式是最简分式5. 如图,四边形的对角线交于点O,下列哪组条件能判断四边形是平行四边形( ) A、 , B、 , C、 , D、 ,6. “按情就是命令,防控就是责任!”在去年新冠肺炎疫情爆发期间,我区教师发扬不畏艰险、无私奉献的精神,挺身而出,协助社区做好疫情监测、排查、防控等工作.现将50名教师参加社区工作时间 (单位:天)的情况统计如下:
A、 , B、 , C、 , D、 ,6. “按情就是命令,防控就是责任!”在去年新冠肺炎疫情爆发期间,我区教师发扬不畏艰险、无私奉献的精神,挺身而出,协助社区做好疫情监测、排查、防控等工作.现将50名教师参加社区工作时间 (单位:天)的情况统计如下:时间 (天)
15
25
35
45
教师人数
4
6
7
13
20
下面是对这50名教师参加社区工作时间的推断:
①平均数一定在40~50之间;②平均数可能在40~50之间;③中位数一定是45;④众数一定是50.其中正确的推断是( )
A、①④ B、②③ C、③④ D、②③④7. 以图(1)(以O为圆心,半径为1的半圆)作为“基本图形”,分别经历如下变换,不能得到图(2)的是( )
 A、绕着OB的中点旋转180°即可 B、先绕着点O旋转180°,再向右平移1个单位 C、先以直线AB为对称轴进行翻折,再向右平移1个单位 D、只要向右平移1个单位8. 如图所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )
A、绕着OB的中点旋转180°即可 B、先绕着点O旋转180°,再向右平移1个单位 C、先以直线AB为对称轴进行翻折,再向右平移1个单位 D、只要向右平移1个单位8. 如图所示,吴伯伯家一块等边三角形的空地ABC,已知点E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围成一圈放养小鸡,则需要篱笆的长是( )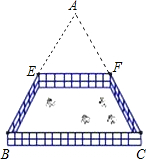 A、15米 B、20米 C、25米 D、30米9. 利用计算器求一组数据的平均数.其按键顺序如下:
A、15米 B、20米 C、25米 D、30米9. 利用计算器求一组数据的平均数.其按键顺序如下: ,则输出的结果为( ) A、1 B、3.5 C、4 D、910. 如图,在平行四边形中,E为上一点,且 , , , , 则下列结论:①;②平行四边形周长是24;③;④;⑤E为中点.正确的结论有( )
,则输出的结果为( ) A、1 B、3.5 C、4 D、910. 如图,在平行四边形中,E为上一点,且 , , , , 则下列结论:①;②平行四边形周长是24;③;④;⑤E为中点.正确的结论有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 计算: .12. 已知2,3,5,m,n五个数据的方差是16,那么3,4,6, , 五个数据的标准差是 .13. 如图,在的正方形格纸中,有一个以格点为顶点的 , 请你找出格纸中所有与成中心对称且也以格点为顶点的三角形共有个;(不包括本身)
 14. 如图,多边形和多边形分别为正六边形和正方形,连接 , 则 .
14. 如图,多边形和多边形分别为正六边形和正方形,连接 , 则 . 15. 如图,在平行四边形中,已知 , , 的平分线交边于点M,则的长为 .
15. 如图,在平行四边形中,已知 , , 的平分线交边于点M,则的长为 . 16. 若关于x的分式方程有增根,则实数m的值是 .17. 如图,将绕点A逆时针旋转120°,得到 . 若点D在线段BC的延长线上,则 .
16. 若关于x的分式方程有增根,则实数m的值是 .17. 如图,将绕点A逆时针旋转120°,得到 . 若点D在线段BC的延长线上,则 . 18. 如图,△ABC的边长AB =3 cm,BC=4 cm,AC=2 cm,将△ABC沿BC方向平移a cm(a<4 cm),得到△DEF,连接AD,则阴影部分的周长为cm.
18. 如图,△ABC的边长AB =3 cm,BC=4 cm,AC=2 cm,将△ABC沿BC方向平移a cm(a<4 cm),得到△DEF,连接AD,则阴影部分的周长为cm. 19. 如图,平行四边形的对角线 , 相交于点O,点E、F分别是线段、的中点,若 , 的周长是18,则 .
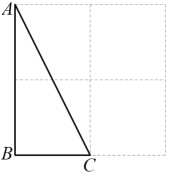
19. 如图,平行四边形的对角线 , 相交于点O,点E、F分别是线段、的中点,若 , 的周长是18,则 . 20. 在的正方形网格中,每个小正方形的顶点称为格点,其中点A,B,C均在格点上,若点A的坐标为 , 请在给定的网格中找出格点E,使以点A、B、C、E为顶点的四边形是平行四边形,则点E的坐标为 .
20. 在的正方形网格中,每个小正方形的顶点称为格点,其中点A,B,C均在格点上,若点A的坐标为 , 请在给定的网格中找出格点E,使以点A、B、C、E为顶点的四边形是平行四边形,则点E的坐标为 .
三、解答题
-
21. 因式分解(1)、(2)、22. 先化简 , 然后在2,-2,-1中选一个你认为合适的a值,代入求值.23. 解方程:24.(1)、如图,以线段、为邻边,用尺规作图画出平行四边形(保留作图痕迹),并说明它用了平行四边形的哪个判定方法?
 (2)、连接、 , 若 , , , 求平行四边形的面积.25. “你怎么样,中国便是怎么样;你若光明,中国便不黑暗”.2020年,一场新冠肺炎疫情牵扯着所有人的心,各界人士齐心协力,众志成城.针对防控资源紧缺问题,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有7人不能到厂生产,为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变.原来每天能生产防护服800套,现在每天能生产防护服650套.(1)、求原来生产防护服的工人有多少人?(2)、复工7天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时.公司决定将复工后生产的防护服15000套捐献给某地,则至少还需要生产多少天才能完成任务?26. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:
(2)、连接、 , 若 , , , 求平行四边形的面积.25. “你怎么样,中国便是怎么样;你若光明,中国便不黑暗”.2020年,一场新冠肺炎疫情牵扯着所有人的心,各界人士齐心协力,众志成城.针对防控资源紧缺问题,某医疗设备公司紧急复工,但受疫情影响,医用防护服生产车间仍有7人不能到厂生产,为了应对疫情,已复产的工人加班生产,由原来每天工作8小时增加到10小时,每小时完成的工作量不变.原来每天能生产防护服800套,现在每天能生产防护服650套.(1)、求原来生产防护服的工人有多少人?(2)、复工7天后,未到的工人同时到岗加入生产,每天生产时间仍然为10小时.公司决定将复工后生产的防护服15000套捐献给某地,则至少还需要生产多少天才能完成任务?26. 在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题: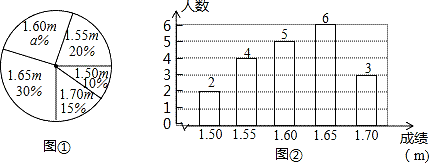 (1)、图1中a的值为;(2)、求统计的这组初赛成绩数据的平均数、众数和中位数;(3)、根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
(1)、图1中a的值为;(2)、求统计的这组初赛成绩数据的平均数、众数和中位数;(3)、根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.

