山东省青岛市市北区2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 在数字 $\frac{22}{7}$ ，3.33， $\frac{π}{2}$ ， $- 2 \frac{1}{2}$ ，0， $\sqrt[3]{\frac{1}{27}}$ ， $- \sqrt{0.9}$ ，2.121121112…（相邻两个2之间1的个数逐次多1）中，无理数的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列几组数据能作为直角三角形的三边长的是( )

A、2，3，4 B、5，3，4 C、4，6，9 D、5，11，13

查看试题解析
3. 点 $P (3, - 5)$ 关于x轴对称的点的坐标为（）

A、 $(- 3, - 5)$ B、 $(5, 3)$ C、 $(- 3, 5)$ D、 $(3, 5)$

查看试题解析
4. 如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含30°角的直角三角板的斜边与纸条一边重合，含45°角的三角板的一个顶点在纸条的另一边上，则∠1的度数是（　　）

A、30° B、20° C、15° D、14°

查看试题解析
5. 有9名同学参加歌咏比赛，他们的预赛成绩各不相同，现取其中前4名参加决赛，小红同学在知道自己成绩的情况下，要判断自己能否进入决赛，还需要知道这9名同学成绩的（）

A、中位数 B、众数 C、平均数 D、加权平均数

查看试题解析
6. 点 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ 是一次函数 $y = - 3 x + 4$ 图像上的两点．若 $x_{1} < x_{2}$ ，则 $y_{1}$ 与 $y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} = y_{2}$ C、 $y_{1} < y_{2}$ D、不能确定

查看试题解析
7. 某校有两种类型的学生宿舍30间，大宿舍每间可住8人，小宿舍每间可住5人．该校198个住宿生恰好住满30间宿舍．设大宿舍有x间，小宿舍有y间，得方程组：（）

A、 ${\begin{array}{l} 5 x + 8 y = 198 \\ x + y = 30 \end{array}$ B、 ${\begin{array}{l} 8 x + 5 y = 198 \\ x + y = 30 \end{array}$ C、 ${\begin{array}{l} x + y = 198 \\ 8 x + 5 y = 30 \end{array}$ D、 ${\begin{array}{l} x + y = 198 \\ 5 x + 8 y = 30 \end{array}$

查看试题解析
8. 设 $b > a$ ，将一次函数 $y = a x + b$ 与 $y = b x + a$ 的图象画在同一平面直角坐标系中，则有组a，b的取值，使得下列四个备选答案中有一个是正确的，则这个正确的答案是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. $\sqrt{9}$ 的平方根是

查看试题解析
10. 如图，直线 $a ∥ b$ ，则 $∠ A$ 的度数是．

查看试题解析
11. 如图，5个大小形状完全相同的长方形纸片，在直角坐标系中摆成如图图案，已知点 $B (- 10 ， 7)$ ，则点A的坐标是．

查看试题解析
12. 如图，在 $Δ A B C$ 和 $Δ A D E$ 中， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C$ ， $A D = A E$ ， C，D，E三点在同一条直线上，连接BD，则下列结论正确的是．
①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE²=2（AD²+AB²）-CD² ．

查看试题解析
13. 如图，直线 $l_{1} ： y = x + 2$ 与直线 $l_{2} ： y = k x + b$ 相交于点 $P (m ， 4)$ ，则方程组 ${\begin{array}{l} y = x + 2 \\ y = k x + b \end{array}$ 的解是．

查看试题解析
14. 正方形A₁B₁C₁O，A₂B₂C₂C₁ ， A₃B₃C₃C₂ ， …按如图方式放置，点A₁、A₂、A₃…和点C₁、C₂、C₃…分别在直线 $y = k x + b (k > 0)$ 和x轴上．已知点B₁（1，1）、B₂（3，2），请写出点Bn的坐标是．

查看试题解析

三、解答题

15. 如图，在平面直角坐标系中，△ABC的顶点A(0，1)，B(2，0)，C(4，4)均在正方形网格的格点上．

(1)、画出△ABC关于x轴对称的图形△A₁B₁C₁并写出顶点A₁ ， B₁ ， C₁的坐标；

(2)、已知P为y轴上一点，若△ABP与△ABC的面积相等，请直接写出点P的坐标．

查看试题解析
16. 计算题

(1)、 $(3 + \sqrt{5})^{2} - (2 - 3 \sqrt{5}) (2 + 3 \sqrt{5})$

(2)、 $(\sqrt{12} - 2 \sqrt{\frac{1}{3}} + \sqrt{48}) \div (2 \sqrt{3})$

查看试题解析
17. 解方程组：

(1)、 ${\begin{array}{l} 2 x + 3 y = 16 \\ x + 4 y = 13 \end{array}$

(2)、 ${\begin{array}{l} 3 x - 4 y = 6 \\ \frac{x}{2} + \frac{y}{3} = 3 \end{array}$ ．

查看试题解析
18. 某社区从不同住宅楼中随机选取了200名居民，调查社区居民双休日的学习状况，并将得到的数据制成扇形统计图（如图①）和频数分布直方图（如图②）．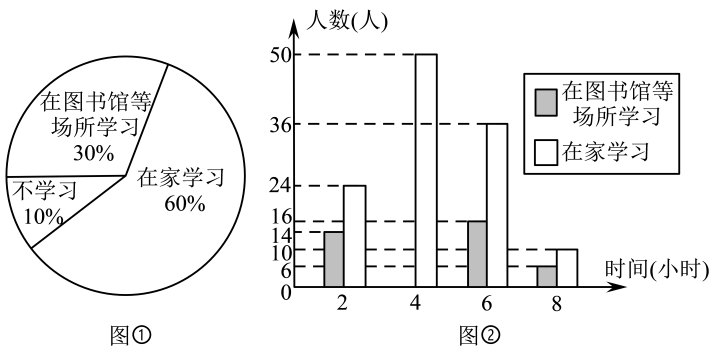

(1)、在这个调查中，200名居民双休日在家学习的有人；

(2)、在这个调查中，在图书馆等场所学习的居民学习时间的平均数和众数分别是多少？

(3)、估计该社区2000名居民双休日学习时间不少于4小时的人数．

查看试题解析
19. 已知：如图，点D、E、F、G都在△ABC的边上，DE∥AC，且∠1+∠2＝180°

(1)、求证：AD∥FG；

(2)、若DE平分∠ADB，∠C＝40°，求∠BFG的度数．

查看试题解析
20. 如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触地面，然后将绳子末端拉到距离旗杆 $8 m$ 处，发现此时绳子末端距离地面 $2 m$ ，请你求出旗杆的高度（滑轮上方的部分忽略不计）．

查看试题解析
21. 抗疫期间，社会各界众志成城，某乳品公司向疫区捐献牛奶，若由铁路运输每千克需运费0.58元；若由公路运输每千克需运费0.28元，并且还需其他费用600元．

(1)、若该公司运输第一批牛奶共计8000千克，分别由铁路和公路运输，费用共计4340元，请问铁路和公路各运输了多少千克牛奶？

(2)、设该公司运输第二批牛奶x（千克），选择铁路运输时，所需费用为 $y_{1}$ （元），选择公路运输时，所需费用 $y_{2}$ （元），请分别写出 $y_{1}$ （元）， $y_{2}$ （元）与x（千克）之间的关系式；

(3)、运输第二批牛奶时公司决定只选择一种运输方式，请问随着x（千克）的变化，怎样选择运输方式所需费用较少？

查看试题解析
22. 快车和慢车分别从A市和B市两地同时出发，匀速行驶，先相向而行，慢车到达A市后停止行驶，快车到达B市后，立即按原路原速度返回A市（调头时间忽略不计），结果与慢车同时到达A市．快、慢两车距B市的路程y₁、y₂（单位：km）与出发时间x（单位：h）之间的函数图象如图所示．

(1)、A市和B市之间的路程是km；

(2)、求a的值，并解释图中点M的横坐标、纵坐标的实际意义；

(3)、快车与慢车迎面相遇以后，再经过多长时间两车相距20km？

查看试题解析
23. Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点.令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α.

(1)、若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2=°；

(2)、若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为：；

(3)、若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由.

(4)、若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间的关系为：.

查看试题解析
24. 一次函数 $y = - \frac{\sqrt{3}}{3} x + 1$ 的图象与x轴、y轴分别交于点A、B，以 $A B$ 为边在第一象限内做等边 $△ A B C$

(1)、求 $△ A B C$ 的面积和点C的坐标；

(2)、如果在第二象限内有一点 $P (a ， \frac{1}{2})$ ，试用含a的代数式表示四边形 $A B P O$ 的面积．

(3)、在x轴上是否存在点M，使 $△ M A B$ 为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

查看试题解析