吉林省白城市大安市2022-2023学年八年级上学期期末数学试题
试卷更新日期:2023-01-06 类型:期末考试
一、单选题
-
1. “喜迎党的二十大召开”,这九个汉字中是轴对称图形的有( )个A、1 B、2 C、3 D、42. 下列每组数分别是三根木棒的长度,能用它们首尾相连摆成一个三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、5cm,5cm,11cm D、13cm,12cm,20cm3. 如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )

A、30° B、40° C、50° D、60°4. 如图,红红书上的三角形被墨迹污染了一部分,她根据所学的知识很快就画了一个与书上完全一样的三角形,那么红红画图的依据是( )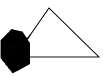 A、SSS B、SAS C、ASA D、AAS5. 计算: 的结果是( )A、 B、 C、 D、6. 下列各式从左到右的变形一定正确的是( )A、= B、=x-y C、= D、=
A、SSS B、SAS C、ASA D、AAS5. 计算: 的结果是( )A、 B、 C、 D、6. 下列各式从左到右的变形一定正确的是( )A、= B、=x-y C、= D、=二、填空题
-
7. 分解因式: .8. “KN95”口罩能过滤空气中95%的直径约为 的非油性颗粒,数据0.0000003用科学记数法表示为.9. 已知△ABC中,∠A=∠B=∠C,则△ABC是 三角形.10. 计算 的结果是.11. 一个多边形的内角和比它的外角和的3倍少180°,则这个多边形的边数是.12. 如图,在中, , , , 则 .
 13. 等腰三角形一边长为5,另一边长为7,则周长为.14. 如图,∠A=∠D , 要使△ABC≌△DBC , 还需要补充一个条件:(填一个即可).
13. 等腰三角形一边长为5,另一边长为7,则周长为.14. 如图,∠A=∠D , 要使△ABC≌△DBC , 还需要补充一个条件:(填一个即可).
三、解答题
-
15. 先化简,再求值 , 其中 .16. 解方程:17. 如图, , , 、 相交于点 .求证: .
 18. 计算: .19. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2).
18. 计算: .19. 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,1),C(-1,2).
( 1 )在图中作出△ABC关于x轴的对称图形△A1B1C1;
( 2 )请直接写出点C关于y轴的对称点C'的坐标: ▲ ;
( 3 )求出△ABC的面积;
( 4 )在y轴上找一点P,使得△PAC周长最小.(保留作图痕迹)
20. 如图,在中, , 平分 , , 垂足为D,其中 , , (1)、求的长度(2)、求的面积.21. 已知m-n=6,mn=4.(1)、求m2+n2的值.(2)、求(m+2)(n-2)的值.22. 新冠肺炎疫情防控期间,学校为做好预防性消毒工作,开学初购进A、B两种消毒液,其中A消毒液的单价比B消毒液的单价多40元,用3200元购买B消毒液的数量是用2400元购买A消毒液数量的2倍,求两种消毒液的单价.23. 在中, , , 过点C作直线 , 于点M,于点N.
(1)、求的长度(2)、求的面积.21. 已知m-n=6,mn=4.(1)、求m2+n2的值.(2)、求(m+2)(n-2)的值.22. 新冠肺炎疫情防控期间,学校为做好预防性消毒工作,开学初购进A、B两种消毒液,其中A消毒液的单价比B消毒液的单价多40元,用3200元购买B消毒液的数量是用2400元购买A消毒液数量的2倍,求两种消毒液的单价.23. 在中, , , 过点C作直线 , 于点M,于点N.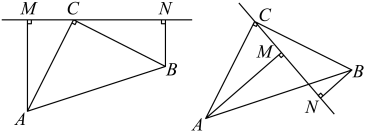 (1)、若在外(如图1),求证:;(2)、若与线段相交(如图2),且 , , 则 .24.(1)、计算并观察下列各式:
(1)、若在外(如图1),求证:;(2)、若与线段相交(如图2),且 , , 则 .24.(1)、计算并观察下列各式:第1个:;
第2个:;
第3个:;
……
这些等式反映出多项式乘法的某种运算规律.
(2)、猜想:若n为大于1的正整数,则;(3)、利用(2)的猜想计算: .(4)、拓广与应用: .25. 为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.(1)、甲、乙两种套房每套提升费用各多少万元?(2)、如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有哪几种方案?26. 如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.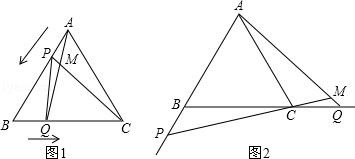 (1)、求证:△ABQ≌△CAP;(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
(1)、求证:△ABQ≌△CAP;(2)、当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.(3)、如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.