广东省阳江市2022-2023学年八年级上学期期末数学试题

试卷更新日期：2023-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个交通标志图中为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{1}{x - 3}$ 有意义，则x的取值范围是（）

A、 $x > 3$ B、 $x < 3$ C、 $x = 3$ D、 $x \neq 3$

查看试题解析
3. 下列由左到右的变形，属于因式分解的是（）

A、 $x^{2} - 4 = (x + 2) (x - 2)$ B、 $(x + 2) (x - 2) = x^{2} - 4$ C、 $x^{2} - 4 + 3 x = (x + 2) (x - 2) + 3 x$ D、 $x^{2} + 4 x - 2 = x (x + 4) - 2$

查看试题解析
4. 下列计算正确的是（）

A、 $x^{6} \div x^{2} = x^{4}$ B、 $2 x^{2} \cdot 3 x^{3} = 6 x^{6}$ C、 $x^{6} y^{2} \div x^{2} y = x^{4}$ D、 $(x + y)^{2} = x^{2} + y^{2}$

查看试题解析
5. 已知一个多边形的内角和等于900º，则这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
6. 计算 $(- 2)^{101} \times {(\frac{1}{2})}^{100}$ 的结果是（）

A、 $- 1$ B、 $1$ C、 $2$ D、 $- 2$

查看试题解析
7. 如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD=2，则点P到边OA的距离是（）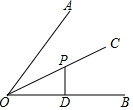

A、1 B、2 C、 $\sqrt{3}$ D、4

查看试题解析
8. 如图，在△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，则CD等于（　　）

A、3 B、4 C、5 D、6

查看试题解析
9. 如图，已知等腰三角形 $A B C$ ， $A B = A C$ ，若以点B为圆心， $B C$ 长为半径画弧，交腰 $A C$ 于点E，则下列结论一定正确的是（）

A、 $∠ E B C = ∠ B A C$ B、 $∠ E B C = ∠ A B E$ C、 $B E = E C$ D、 $B C = C E$

查看试题解析
10. 如图， $A D$ 是 $△ A B C$ 的中线，E，F分别是 $A D$ 和 $A D$ 延长线上的点，且 $D E = D F$ ，连接 $B F$ ， $C E$ ，下列说法：① $△ A B D$ 和 $△ A C D$ 面积相等；② $∠ B A D = ∠ C A D$ ；③ $△ B D F ≅ △ C D E$ ；④ $B F ∥ C E$ ；⑤ $C E = A E$ ．其中正确的是（　　）

A、①② B、③⑤ C、①③④ D、①④⑤

查看试题解析

二、填空题

11. 计算： ${(3 - π)}^{0} + 2^{- 1} =$ ．

查看试题解析
12. 若 $x^{2} + k x + 9$ 是完全平方式，则k的值为．

查看试题解析
13. 在 $△ A B C$ 中， $A B = A C$ ， $A B$ 的垂直平分线交 $A C$ 于D，交 $A B$ 于E，连接 $B D$ ，若 $∠ A D E = 40 °$ ，则 $∠ D B C =$ ．

查看试题解析
14. 若 ${(x + y)}^{2} = 12$ ， ${(x - y)}^{2} = 8$ ，则xy= ．

查看试题解析
15. 如图，在锐角三角形ABC中，AC＝6，△ABC的面积为15，∠BAC的平分线交BC于点D ， M ， N分别是AD和AB上的动点，则BM+MN的最小值是．

查看试题解析

三、解答题

16.

(1)、解分式方程： $\frac{2}{x - 3} = \frac{3}{x}$ ；

(2)、分解因式： $x^{2} - 4 x$ ．

查看试题解析
17. 先化简，再求值： $(x - 1 + \frac{1}{x + 1}) \cdot \frac{x^{2} + 2 x + 1}{x}$ ，其中 $x = 3$ ．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ．

(1)、用尺规作 $∠ A B C$ 的平分线BD，交AC于点D．（保留作图痕迹，不写作法）

(2)、若 $∠ A = 30 °$ ，求证： $A D = B D$ ．

查看试题解析
19. 我们知道几个非负数的和等于0，只有这几个数同时等于0才成立，如 $| x - 2 | + {(y + 3)}^{2} = 0$ ，因为 $| x - 2 |$ ， ${(y + 3)}^{2}$ 都是非负数，则 $x - 2 = 0$ ， $y + 3 = 0$ ，即可求 $x = 2$ ， $y = - 3$ ，应用知识解决下列各题：

(1)、若 ${(x + 4)}^{2} + {(y - 3)}^{2} = 0$ ，则x= ， y=；

(2)、若 $x^{2} + y^{2} - 2 x + 4 y = - 5$ ，则 $x^{y} =$ ；

(3)、若 $x^{2} + 3 y^{2} + 4 x - 6 y = - 7$ ，求 ${(x + y)}^{2022}$ 的值．

查看试题解析
20. 如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，两线相交于F点.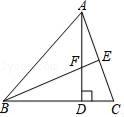

(1)、若∠BAC=60°，∠C=70°，求∠AFB的大小；

(2)、若D是BC的中点，∠ABE=30°，求证：△ABC是等边三角形.

查看试题解析
21. 惠阳区某中学2016年在商场购买甲、乙两种不同的足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元

(1)、求购买一个甲种足球，一个乙种足球各需多少元？

(2)、2017年为响应习总书记“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个，预算金额不超过3000元.去到商场时恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果该学校此次需购买20个乙种足球，请问该学校购买这批足球所用金额是否会超过预算？

查看试题解析
22. 如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．

(1)、若△A₁B₁C₁与△ABC关于y轴成轴对称，则△A₁B₁C₁三个顶点坐标分别为A₁ ， B₁ ， C₁；

(2)、在x轴上找一点P，使PA+PB的值最小，请直接写出点P的坐标是．

(3)、在y轴上是否存在点Q．使得S_△_ACQ＝ $\frac{1}{2}$ S_△_ABC ，如果存在，求出点Q的坐标，如果不存在，说明理由．

查看试题解析
23. 如图，已知 $A (3 ， 0)$ ， $B (0 ， - 1)$ ，连接 $A B$ ，过B点作 $A B$ 的垂线段 $B C$ ，使 $B A = B C$ ，连接 $A C$ ．

(1)、如图1，求C点坐标；

(2)、如图2，若P点从A点出发沿x轴向左平移，连接 $B P$ ，作等腰直角 $△ B P Q$ ，连接 $C Q$ ，当点P在线段 $O A$ 上，求证： $P A = C Q$ ．

查看试题解析