广东省茂名市电白区2022-2023学年八年级上学期数学期末试题
试卷更新日期:2023-01-06 类型:期末考试
一、单选题
-
1. 在实数 , , , , 0中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 如图,老师在黑板上建立平面直角坐标系,并把课本放在如图所示的位置,则一定没有被课本遮住的点是( )
 A、 B、 C、 D、3. 如图,一根长为的竹竿斜靠在竖直的墙壁上,竹竿底端B离墙壁距离 , 则该竹竿的顶端A离地竖直高度为( )
A、 B、 C、 D、3. 如图,一根长为的竹竿斜靠在竖直的墙壁上,竹竿底端B离墙壁距离 , 则该竹竿的顶端A离地竖直高度为( )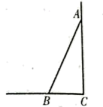 A、 B、 C、 D、4. 某次数学测验中,八(1)班55人平均分为80分,八(2)班45人平均分为70分,则这两个班总平均分为( )A、75分 B、75.5分 C、76分 D、76.5分5. 小颖的爸爸要在某条街道l上修建一个奶站P,向居民区A,B提供牛奶,要使点P到A,B的距离之和最短,则下列作法正确的是( )A、
A、 B、 C、 D、4. 某次数学测验中,八(1)班55人平均分为80分,八(2)班45人平均分为70分,则这两个班总平均分为( )A、75分 B、75.5分 C、76分 D、76.5分5. 小颖的爸爸要在某条街道l上修建一个奶站P,向居民区A,B提供牛奶,要使点P到A,B的距离之和最短,则下列作法正确的是( )A、 B、
B、 C、
C、 D、
D、 6. 已知方程组的解满足 , 则k的值是( )A、 B、 C、 D、7. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、
6. 已知方程组的解满足 , 则k的值是( )A、 B、 C、 D、7. 下列各图中,当a∥b时,符合∠1=∠2+∠3关系的是( )A、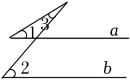 B、
B、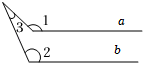 C、
C、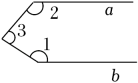 D、
D、 8. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( )
8. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( ) A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h9. 甲乙两辆小车同时从A地开出,甲车比乙车每小时快 , 结果甲车行驶了40分钟到达了B地,而乙车比甲车晚5分钟到达B地,设甲车和乙车的速度分别为 , , 则下列方程组正确的是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,长方形ABCD的顶点坐标分别为A(-1,2),B(-1,-1),C(1,-1),D(1,2),点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度.记P,Q在长方形边上第1次相遇时的点为M1 , 第二次相遇时的点为M2 , 第三次相遇时的点为M3 , …,则点M2022的坐标为( )
A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h9. 甲乙两辆小车同时从A地开出,甲车比乙车每小时快 , 结果甲车行驶了40分钟到达了B地,而乙车比甲车晚5分钟到达B地,设甲车和乙车的速度分别为 , , 则下列方程组正确的是( )A、 B、 C、 D、10. 如图,在平面直角坐标系中,长方形ABCD的顶点坐标分别为A(-1,2),B(-1,-1),C(1,-1),D(1,2),点P从点A出发,沿长方形的边顺时针运动,速度为每秒2个单位长度,点Q从点A出发,沿长方形的边逆时针运动,速度为每秒3个单位长度.记P,Q在长方形边上第1次相遇时的点为M1 , 第二次相遇时的点为M2 , 第三次相遇时的点为M3 , …,则点M2022的坐标为( ) A、(1,0) B、(-1,0) C、(1,2) D、(0,-1)
A、(1,0) B、(-1,0) C、(1,2) D、(0,-1)二、填空题
-
11. 求值: .12. 如图,直线OA的解析式是 .
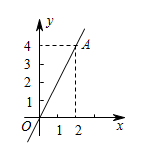 13. 已知点M(-2,5),点N(2b-a,a+b),若点N在第一象限,MN所在直线平行于x轴,且M、N两点之间的距离为6,则ab的值为 .14. 某图书出租店图书的租金y(元)与出租的天数x(天)之间的函数图象如图所示,结合图象计算可知:两天后每过一天租金增加元.
13. 已知点M(-2,5),点N(2b-a,a+b),若点N在第一象限,MN所在直线平行于x轴,且M、N两点之间的距离为6,则ab的值为 .14. 某图书出租店图书的租金y(元)与出租的天数x(天)之间的函数图象如图所示,结合图象计算可知:两天后每过一天租金增加元. 15. 下列命题:①若|a|=-a,则a<0;②内错角相等;③平行于同一条直线的两条直线平行;④直线a、b、c在同一平面内,若a⊥b,a⊥c,则bc;⑤实数包括有理数和无理数.其中正确的命题序号有 .
15. 下列命题:①若|a|=-a,则a<0;②内错角相等;③平行于同一条直线的两条直线平行;④直线a、b、c在同一平面内,若a⊥b,a⊥c,则bc;⑤实数包括有理数和无理数.其中正确的命题序号有 .三、解答题
-
16. 解二元一次方程组:17. 已知 , 求的平方根.18. A、B两地的路段有一段上坡路和一段下坡路组成,某人步行的速度是:上坡4km/h、下坡5km/h,此人从A地到B地花了5h,从B返回A地时花了4.9h,求A、B两地的距离.19. 如图,在中,D为上一点,E为中点,连接DE并延长至点F,使得 , 连接 .
 (1)、求证:;(2)、若 , 连接平分平分 , 求的度数.20. 新华学校团支部发起了以“完善自我,服务社会:关爱弱势,大写人生”为主题的志愿活动,鼓励和倡导大家在暑假期间积极参加志愿活动,开学后该校团支部抽取了部分学生进行调查,并对他们参加志愿活动的次数进行了统计,根据调查情况绘制成的统计图表如下:
(1)、求证:;(2)、若 , 连接平分平分 , 求的度数.20. 新华学校团支部发起了以“完善自我,服务社会:关爱弱势,大写人生”为主题的志愿活动,鼓励和倡导大家在暑假期间积极参加志愿活动,开学后该校团支部抽取了部分学生进行调查,并对他们参加志愿活动的次数进行了统计,根据调查情况绘制成的统计图表如下:被抽取学生参加志愿活动的次数统计表:
次数
1
2
3
4
5
6
人数
1
2
a
6
b
2
被抽取学生参加志愿服务活动的次数扇形统计图
 (1)、a= , b= ;(2)、这组数据的中位数和众数各是多少?(3)、若该校初二年级共有700名学生,请估计初二年级中参加志愿活动在4次及以上的学生人数.21. 如图,直线=kx+b与坐标轴交于A(0,2),B(m,0)两点,与直线=-4x+12交于点P(2,n),直线=-4x+12交x轴于点C,交y轴于点D.
(1)、a= , b= ;(2)、这组数据的中位数和众数各是多少?(3)、若该校初二年级共有700名学生,请估计初二年级中参加志愿活动在4次及以上的学生人数.21. 如图,直线=kx+b与坐标轴交于A(0,2),B(m,0)两点,与直线=-4x+12交于点P(2,n),直线=-4x+12交x轴于点C,交y轴于点D. (1)、求m,n值;(2)、直接写出方程组的解为;(3)、求△PBC的面积.
(1)、求m,n值;(2)、直接写出方程组的解为;(3)、求△PBC的面积.

