北京市丰台区2022~2023学年八年级上学期期末数学试卷

试卷更新日期：2023-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图形分别是四届国际数学家大会的会标，其中不属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 随着科技不断发展，芯片的集成度越来越高．我国企业中芯国际已经实现14纳米量产，14纳米等于0.000014毫米，将0.000014用科学记数法表示应为（）．

A、 $14 \times 1 0^{- 6}$ B、 $1.4 \times 1 0^{- 5}$ C、 $1.4 \times 1 0^{- 4}$ D、 $0.14 \times 1 0^{- 4}$

查看试题解析
3. 已知三角形的两边长分别为5cm和8cm，则第三边的长可以是（）

A、2cm B、3cm C、6cm D、13cm

查看试题解析
4. 下列计算正确的是（）

A、 $a + a = a^{2}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 $a^{3} \div a^{2} = a$ D、 $(2 a)^{3} = 6 a^{3}$

查看试题解析
5. 等腰三角形的一个角是 $80 °$ ，它的底角的大小为（）

A、 $80 °$ B、 $50 °$ C、 $80 °$ 或 $20 °$ D、 $80 °$ 或 $50 °$

查看试题解析
6. 若a≠b，则下列分式变形正确的是（）

A、 $\frac{a + 1}{b + 1} = \frac{a}{b}$ B、 $\frac{a - 1}{b - 1} = \frac{a}{b}$ C、 $\frac{a^{2}}{b^{2}} = \frac{a}{b}$ D、 $\frac{2 a}{2 b} = \frac{a}{b}$

查看试题解析
7. 如图，在△ABC中，∠C=90°，∠A=30°，以点B为圆心，适当长为半径的画弧，分别交BA，BC于点M、N；再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线BP交AC于点D，则下列说法中错误的是（）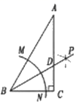

A、BP是∠ABC的平分线 B、AD=BD C、 $S_{△ C B D} ： S_{△ A B D} = 1 ： 3$ D、CD= $\frac{1}{2}$ BD

查看试题解析
8. 我们在观看台球比赛时，发现选手们常常会用反弹的技巧击打目标球．在此过程中，撞击路线与桌边的夹角等于反射路线与桌边的夹角，如图1， $∠ 1 = ∠ 2$ ．如图2，建立平面直角坐标系 $x O y$ ，已知A球位于点 $(1 ， 2)$ 处，B球位于点 $(6 ， 1)$ 处．现击打A球，使A球向桌边的整点位置（横纵坐标均为整数，球洞位置不可反弹）撞击，若A球最多在台球桌边反弹两次后击中B球，则满足条件的桌边整点有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 若 $\frac{\sqrt{x}}{x - 3}$ 有意义，则x的取值范围是．

查看试题解析
10. 在平面直角坐标系 $x O y$ 中，点 $A (- 2 ， 3)$ 与点B关于x轴对称，则点B的坐标是．

查看试题解析
11. 分解因式： $x - x^{3} =$ ，

查看试题解析
12. 如图，已知 $∠ B = ∠ D = 90 °$ ，请添加一个条件（不添加辅助线），使 $△ A B C ≌ △ A D C$ ，依据是．

查看试题解析
13. 若一个正多边形的每一个外角都是30°，则这个正多边形的边数为．

查看试题解析
14. 如图1，在边长为a的大正方形中，剪去一个边长为3的小正方形，将余下的部分按图中的虚线剪开后，拼成如图2所示的长方形．根据两个图形阴影部分面积相等的关系，可以列出的等式为．

查看试题解析
15. 如图， $A D$ 是等边三角形 $A B C$ 的中线， $A E = A D$ ，则 $∠ E D C$ 的度数为．

查看试题解析
16. 欧拉是18世纪瑞士著名的数学家，他的贡献不仅遍及高等数学的各个领域，在初等数学中也留下了他的足迹．下面是关于分式的欧拉公式：
$\frac{a^{r}}{(a - b) (a - c)} + \frac{b^{r}}{(b - c) (b - a)} + \frac{c^{r}}{(c - a) (c - b)} = {\begin{cases} p ， & r = 0 时 \\ 0 ， & r = 1 时 \\ 1 ， & r = 2 时 \\ a + b + c ， & r = 3 时 \end{cases}$

（其中a，b，c均不为零，且两两互不相等）．

(1)、当 $r = 0$ 时，常数p的值为．

(2)、利用欧拉公式计算： $\frac{202 2^{3}}{2} - 202 1^{3} + \frac{202 0^{3}}{2} =$ ．

查看试题解析

三、解答题

17. 计算： $| - 4 | + 3^{- 2} - （ π - 2022 ）^{0}$ ．

查看试题解析
18. 计算： $(a + 5) (a - 5) - 3 a (a - 1)$ ．

查看试题解析
19. 计算： $(1 - \frac{1}{m - 2}) \div \frac{m^{2} - 6 m + 9}{m - 2}$ ．

查看试题解析
20. 已知：如图，点 $A$ ， $D$ ， $C$ 在同一直线上， $A B // C E$ ， $A C = C E$ ， $∠ B = ∠ C D E$ ．求证： $B C = D E$ ．

查看试题解析
21. 先化简，再求值 $(x - 1) (x - 2) - {(x + 1)}^{2}$ ，其中x= $\frac{1}{2}$ ．

查看试题解析
22. 解方程： $\frac{x}{x + 1} + 1 = \frac{5}{2 x + 2}$ ．

查看试题解析
23. 下面是小明同学设计的“作一个角等于已知角的2倍”的尺规作图的过程．
已知：如图1， $∠ A O B$ ．
求作： $∠ A D C$ ，使 $∠ A D C = 2 ∠ A O B$ ，且点D在射线 $O A$ 上．
作法：
①如图2，在射线 $O B$ 上任取一点C；
②作线段 $O C$ 的垂直平分线 $M N$ ，交 $O A$ 于点D；
③连接 $D C$ ．
则 $∠ A D C$ 即为所求作的角．
根据上述作图过程，回答问题：

(1)、用直尺和圆规，补全图2中的图形（保留作图痕迹）；

(2)、完成下面的证明：
证明： $∵ M N$ 是线段 $O C$ 的垂直平分线，
$∴ O D =$ ▲ （）（填推理的依据）．
$∴ ∠ A O B = ∠ D C O$ （）（填推理的依据）．
$∵ ∠ A D C = ∠ A O B + ∠ D C O$ ，
$∴ ∠ A D C = 2 ∠ A O B$ ．

查看试题解析
24. 观察下列算式，完成问题：
算式①： $4^{2} - 2^{2} = 12 = 4 \times 3$
算式②： $6^{2} - 4^{2} = 20 = 4 \times 5$
算式③： $8^{2} - 6^{2} = 28 = 4 \times 7$
算式④： $1 0^{2} - 8^{2} = 36 = 4 \times 9$
……

(1)、按照以上四个算式的规律，请写出算式⑤：；

(2)、上述算式用文字表示为：“任意两个连续偶数的平方差都是4的奇数倍”．若设两个连续偶数分别为 $2 n$ 和 $2 n + 2$ （ $n$ 为整数），请证明上述命题成立；

(3)、命题“任意两个连续奇数的平方差都是4的奇数倍”是否成立？若成立，请证明；若不成立，请举出反例．

查看试题解析

25. 小刚家近期准备换车，看中了价格相同的两款车，他对这两款车的部分信息做了调查，如下表所示：

燃油车	新能源车
油箱容积：40升	电池电量：60千瓦时
油价：9元/升	电价：0.6元/千瓦时
续航里程：a千米	续航里程：a千米
每千米行驶费用： $\frac{40 \times 9}{a}$ 元	每千米行驶费用：____元

（续航里程指车辆在最大的能源储备下可连续行驶的总里程）

(1)、表中的新能源车每千米行驶费用为元（用含a的代数式表示）；

(2)、若燃油车的每千米行驶费用比新能源车多0.54元，分别求出两款车每千米行驶费用；

(3)、在（2）的条件下，若燃油车和新能源车每年的其它费用分别为4800元和7500元．每年行驶里程至少超过千米时，使用新能源车的年费用更低（年费用=年行驶费用+年其它费用）．

查看试题解析

26. 在 $△ A B C$ 中， $∠ B A C = 110 °$ ， $A C = A B$ ，射线 $A D$ ， $A E$ 的夹角为 $55 °$ ，过点 $B$ 作 $B F ⊥ A D$ 于点 $F$ ，直线 $B F$ 交 $A E$ 于点 $G$ ，连结 $C G$ ．

(1)、如图1，射线 $A D$ ， $A E$ 都在 $∠ B A C$ 的内部．
①设 $∠ B A D = α$ ，则 $∠ C A G =$ （用含有 $α$ 的式子表示）；
②作点 $B$ 关于直线 $A D$ 的对称点 $B^{'}$ ，则线段 $B^{'} G$ 与图1中已有线段的长度相等；

(2)、如图2，射线 $A E$ 在 $∠ B A C$ 的内部，射线 $A D$ 在 $∠ B A C$ 的外部，其他条件不变，用等式表示线段 $B F$ ， $B G$ ， $C G$ 之间的数量关系，并证明．

查看试题解析
27. 在平面中，对于点M，N，P，若 $∠ M P N = 90 °$ ，且 $P M = P N$ ，则称点P是点M和点N的“垂等点”．在平面直角坐标系 $x O y$ 中，

(1)、已知点 $M (- 3 ， 2)$ ，点 $N (1 ， 0)$ ，则点 $P_{1} (0 ， 3)$ ， $P_{2} (- 2 ， - 1)$ ， $P_{3} (- 5 ， - 2)$ 中是点M和点N的“垂等点”的是；

(2)、已知点 $A (- 4 ， 0)$ ， $B (0 ， b) (b > 0)$ ．
①若在第二象限内存在点C，使得点B是点A和点C的”垂等点”，写出点C的坐标（用含b的式子表示），并说明理由；
②当 $b = 4$ 时，点D，点E是线段 $A O$ ， $B O$ 上的动点（点D，点E不与点A，B，O重合）．若点F是点D和点E的”垂等点”，直接写出点F的纵坐标t的取值范围．

查看试题解析