山东省青岛市莱西市2022-2023学年七年级上学期期末数学试题

试卷更新日期：2023-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. 下面是科学防控新冠知识的图片，其中的图案是轴对称图形（）

A、 B、 C、 D、

查看试题解析
2. 下列图形中，不是运用三角形的稳定性的是(　　)

A、 B、 C、 D、

查看试题解析
3. 下列各组数中，能作为直角三角形三边长的是（）

A、 $2，3，5$ B、 $\sqrt{6} ， \sqrt{8} ， \sqrt{10}$ C、 $8，15，17$ D、 $1 ， \sqrt{2} ， 3$

查看试题解析
4. 用式子表示16的平方根，正确的是（）

A、 $\pm \sqrt{16} = \pm 4$ B、 $\sqrt{16} = 4$ C、 $\sqrt{16} = \pm 4$ D、 $\pm \sqrt{16} = 4$

查看试题解析
5. 如图，根据图中的标注和作图痕迹可知，在数轴上的点 $A$ 所表示的数为（）

A、 $- 1 - \sqrt{5}$ B、 $- 1 + \sqrt{5}$ C、 $- \sqrt{5}$ D、 $1 - \sqrt{5}$

查看试题解析
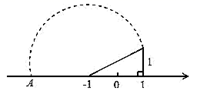6. 下列计算，错误的是（）

A、 ${(- \sqrt{2})}^{2} + {(\sqrt[3]{2})}^{3} = 0$ B、 $\sqrt[3]{- 0.064} = - 0.4$ C、 $\sqrt[3]{{(- 2)}^{3}} = - 2$ D、 $\sqrt{{(\pm 7)}^{2}} = 7$

查看试题解析
7. 如图所示，每个小方格的边长都为1，在直角坐标系中，如果图书馆的横坐标与实验楼的横坐标互为相反数，大门的纵坐标与实验楼的纵坐标互为相反数，则图书馆的坐标是（）

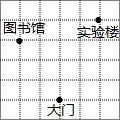A、（1，5） B、（﹣2，3） C、（﹣2，﹣1） D、（﹣2，1）

查看试题解析
8. 甲无人机从地面起飞，乙无人机从距离地面20m高的楼顶起飞，两架无人机同时匀速上升10s．甲、乙两架无人机所在的位置距离地面的高度y（单位：m）与无人机上升的时间x（单位：s）之间的关系如图所示．下列说法正确的是（）

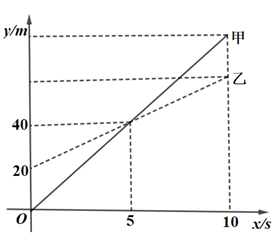A、5s时，两架无人机都上升了40m B、10s时，两架无人机的高度差为20m C、乙无人机上升的速度为8m/s D、10s时，甲无人机距离地面的高度是60m

查看试题解析

二、填空题

9. 下列实数中是无理数的是．
$\sqrt{3}$ ， $\sqrt{{(- 5)}^{2}}$ ， $\sqrt[3]{27}$ ， $\frac{22}{7}$ ， $0.8080080008 ⋯$ （每两个 $8$ 之间依次多一个 $0$ ）．

查看试题解析
10. 如图所示，在直角坐标系内，线段AB垂直于y轴，垂足为B，且AB＝2，如果将线段AB沿y轴翻折，点A落在点C处，那么点C的横坐标是.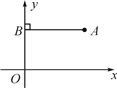

查看试题解析
11. 如图，图形的各个顶点都在3 $\times$ 3正方形网格的格点上.则 $∠ 1 + ∠ 2 =$ .

查看试题解析
12. 已知一次函数的图象过点 $(1 ， 2)$ ，且y随x的增大而减少．请写出一个符合条件的一次函数的解析式：．（写出一个符合条件的解析式即可）

查看试题解析
13. 勾股定理 $a^{2} + b^{2} = c^{2}$ 本身就是一个关于 $a$ ， $b$ ， $c$ 的方程，满足这个方程的正整数解 $(a ， b ， c)$ 通常叫做勾股数组.毕达哥拉斯学派提出了一个构造勾股数组的公式，根据该公式可以构造出如下勾股数组：（3，4，5），（5，12，13），（7，24，25），….分析上面勾股数组可以发现，4=1×（3+1），12=2×（5+1），24=3×（7+1），…分析上面规律，第5个勾股数组为.

查看试题解析
14. 如图，长为12 cm的弹性皮筋拉直放置在一轴上，固定两端A和B，然后把中点C向上拉升8 cm至点D，则弹性皮筋被拉长了cm．

查看试题解析
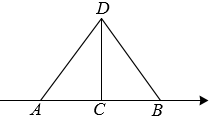15. 甲、乙两人都从光明学校出发，去距离光明学校1500m远的篮球馆打球，他们沿同一条道路匀速行走，乙比甲晚出发4min．设甲行走的时间为t（单位：min），甲、乙两人相距y（单位：m），表示y与t的函数关系的图象如图所示，根据图中提供的信息，下列说法正确的是（填写序号）：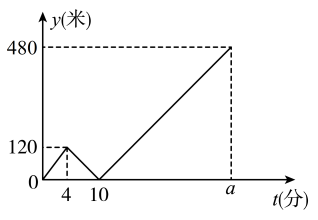
①甲行走的速度为30m/mim；②乙在距光明学校500m处追上了甲；
③甲、乙两人的最远距离是480m；④甲从光明学校到篮球馆走了30min．

查看试题解析
16. 如图，在甲、乙两个大小不同的 $6 \times 6$ 的正方形网格中，正方形 $A B C D$ ， $E F G H$ 分别在两个网格上，且各顶点均在网格线的交点上．若正方形 $A B C D$ ， $E F G H$ 的面积相等，甲、乙两个正方形网格的面积分别记为 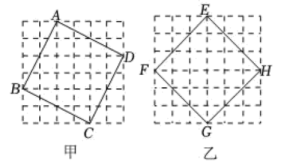$S_{甲}$ ， $S_{乙}$ ，则 $S_{甲} ： S_{乙} =$ ．

查看试题解析

三、解答题

17. 如图，已知 $△ A B C$ ，请根据“ASA”作出 $△ D E F$ ，使 $△ D E F ≌ △ A B C$ ．

查看试题解析
18. 计算

(1)、 $\sqrt{{(- 3)}^{2}} + \sqrt[3]{- 64} - \sqrt{12}$

(2)、 $\sqrt[3]{- 125} - \sqrt{2 \frac{7}{9}} + \sqrt{- {(- \frac{1}{4})}^{3}} + \sqrt[3]{\frac{8}{27}}$

查看试题解析
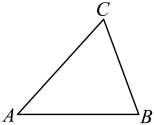19. 如图，已知点C是线段AB的中点，且 $A E = B D$ ， $∠ A = ∠ B$ ． $∠ E$ 与 $∠ D$ 相等吗？请说明理由．

查看试题解析
20. 已知 $x = 1 - 2 a ， y = 3 a - 4$ .

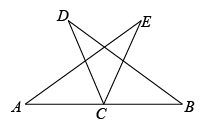(1)、已知x的算数平方根为3，求a的值；

(2)、如果x，y都是同一个数的平方根，求这个数．

查看试题解析
21. 如图，在五边形 $A B C D E$ 中， $A B = D E$ ， $A C = A D$ .

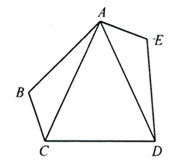(1)、请你添加一个与角有关的条件，使得 $△ A B C ≌ △ D E A$ ，并说明理由；

(2)、在（1）的条件下，若 $∠ C A D = 65 °$ ， $∠ B = 110 °$ ，求 $∠ B A E$ 的度数.

查看试题解析
22. 在某风景游船处，如图，在离水面高度为 $5 m$ 的岸上，有人用绳子拉船靠岸，开始时绳子 $B C$ 的长为 $13 m$ ，此人以 $0.5 m / s$ 的速度收绳． $10 s$ 后船移动到点D的位置，此时船距离岸边多少m?（结果保留根号）

查看试题解析
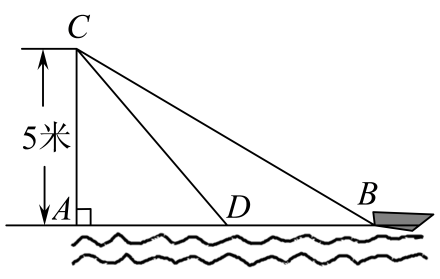23. 在如图所示的直角坐标系中，A，B，C，D都是网格中的格点．

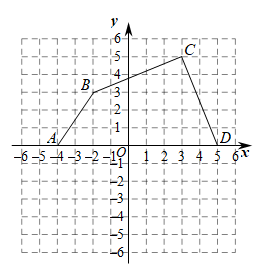(1)、写出点B与点C的坐标；

(2)、若将点B与点C的横坐标保持不变，纵坐标分别乘 $- 1$ ，对应点分别为F，E，连接 $D E ， E F ， F A$ ，则六边形 $A B C D E F$ 有什么特点？

(3)、求四边形 $A B C D$ 的面积．

查看试题解析
24. 如图，过点A的一次函数的图象与正比例函数y＝2x图象相交于点B．

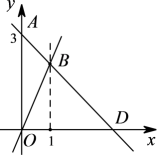(1)、求该一次函数的解析式；

(2)、如果点C（m，－2）在该一次函数的图象上，请求m的值；

(3)、若该一次函数的图象与x轴交于D点，求△BOD的面积．

查看试题解析
25. 如图是某型号新能源纯电动汽车充满电后，蓄电池剩余电量 $y$ （千瓦时）关于已行驶路程 $x$ （千米）的函数图象.

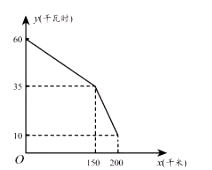(1)、根据图象，直接写出蓄电池剩余电量为35千瓦时时汽车已行驶的路程，当 $0 \leq x \leq 150$ 时，求1千瓦时的电量汽车能行驶的路程；

(2)、当 $150 \leq x \leq 200$ 时求 $y$ 关于 $x$ 的函数表达式，并计算当汽车已行驶180千米时，蓄电池的剩余电量.

查看试题解析
26. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 5$ cm， $B C = 4$ cm，若点P从点A出发，以每秒2cm的速度沿折线 $A - B - C - A$ 运动，设运动时间为 $t (t > 0)$ 秒．

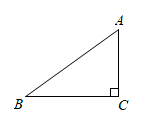(1)、 $A C =$ cm；

(2)、若点P恰好在 $∠ A B C$ 的角平分线上，求此时t的值；

(3)、在运动过程中，当 $t =$ ▲ 值时， $△ A C P$ 为等腰三角形（直接写出结果）

查看试题解析
27. 小华端午节从家里出发，沿笔直道路匀速步行去妈妈经营的商店帮忙，妈妈同时骑三轮车从商店出发，沿相同路线匀速回家装载货物，然后按原路原速返回商店，小华到达商店比妈妈返回商店早5分钟.在此过程中，设妈妈从商店出发开始所用时间为t（分钟），图1表示两人之间的距离s（米）与时间t（分钟）的函数关系的图象；图2中线段 $A B$ 表示小华和商店的距离 $y_{1}$ （米）与时间t（分钟）的函数关系的图象的一部分，请根据所给信息解答下列问题：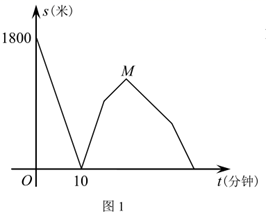

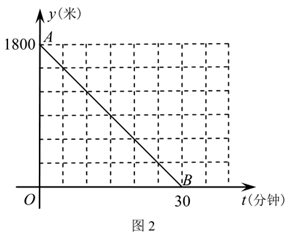(1)、填空：妈妈骑车的速度是米/分钟，妈妈在家装载货物所用时间是分钟，点M的坐标是；

(2)、直接写出妈妈和商店的距离 $y_{2}$ （米）与时间t（分钟）的函数关系式，并在图2中画出其函数图象；

(3)、求t为何值时，两人相距360米.

查看试题解析