吉林省长春市汽开区联盟校区2022-2023学年七年级上学期期末线上检测数学试题

试卷更新日期：2023-01-06 类型：期末考试

进入出卷网下载

一、单选题

1. -5的相反数是（）

A、5 B、-5 C、 $\frac{1}{5}$ D、- $\frac{1}{5}$

查看试题解析
2. 我国天问一号火星探测器于2021年5月15日成功着陆火星表面.经测算，地球跟火星最远距离400000000千米，其中400000000用科学记数法表示为（）

A、 $4 \times 10^{9}$ B、 $40 \times 10^{7}$ C、 $4 \times 10^{8}$ D、 $0.4 \times 10^{9}$

查看试题解析
3. 下列几何体的展开图中，能围成圆柱的是（）

A、 B、 C、 D、

查看试题解析
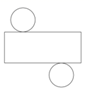4. 将多项式 $- 9 + x^{3} + 3 x y^{2} - x^{2} y$ 按x的降幂排列的结果为（）

A、 $x^{3} + x^{2} y - 3 x y^{2} - 9$ B、 $- 9 + 3 x y^{2} - x^{2} y + x^{3}$ C、 $- 9 - 3 x y^{2} + x^{2} y + x^{3}$ D、 $x^{3} - x^{2} y + 3 x y^{2} - 9$

查看试题解析
5. 如图，直线AB经过点O，射线OA是北偏东40°方向，则射线OB的方位角是（）

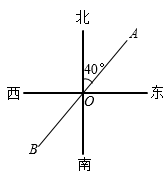A、南偏西50° B、南偏西40° C、北偏西50° D、北偏西40°

查看试题解析
6. 下列计算正确的是（）

A、2x+4x＝8x² B、9x²y﹣9yx²＝0 C、7x²﹣3x²＝4 D、3x+2y＝5xy

查看试题解析
7. 含30°角的直角三角板与直线a，b的位置关系如图所示，已知 $a // b$ ， $∠ 1 = 35 °$ ．则 $∠ A D C$ 的度数是（）

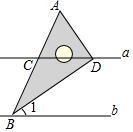A、35° B、45° C、55° D、65°

查看试题解析
8. 如图，点C、D为线段 $A B$ 上的两点， $A C ： C D ： B D = 3 ： 6 ： 4$ ，若 $A B = 13$ ，则 $C D$ 等于（）

A、4 B、5 C、6 D、7

查看试题解析
9. 如图， $A B ∥ C D$ ， $∠ F G B ＝ 155 °$ ， $F G$ 平分 $∠ E F D$ ，则 $∠ B E F$ 的大小为（）

A、 $100 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看试题解析
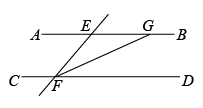10. 按下面图示的程序计算，若开始输入的值x为正数，最后输出的结果为11，则满足条件的正数x有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 若上升15米记作+15米，则下降12米记作

查看试题解析
12. 计算：2a²﹣（a²+2）＝．

查看试题解析
13. 比较大小： $- 2 \frac{1}{3}$ -2.3．（“＞”“＜”或“=”）

查看试题解析
14. 用四舍五入法，对 $0.2356$ 精确到百分位得到的近似数为．

查看试题解析
15. 已知 $∠ A = 23 ° 9^{'}$ ，则 $∠ A$ 的余角是．（用度、分、秒表示）

查看试题解析
16. 如图，点D是线段AB的中点，C是线段AD的中点，若AB＝8cm，则CD＝cm.

查看试题解析
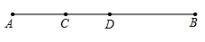17. 某商店经销一种品牌的洗衣机，其中某一型号的洗衣机每台进价为a元，商店将进价提高20%后作为零售价进行销售，一段时间后，商店又以9折优惠价促销，这时该型号洗衣机的零售价为元．

查看试题解析
18. 若 $9 a - 3 b + 1 = 0$ ，则 $3 a - b + 2$ 的值是．

查看试题解析
19. 如图是用棋子摆成的图形，按照这种摆法，第 $n$ 个图形中共有个棋子．

查看试题解析
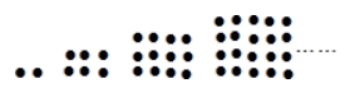20. 将一张长方形纸片按如图所示的方式折叠， $E N$ ， $E M$ 为折痕，折叠后点 $A'$ ， $B'$ ， $E$ 在同一直线上，已知 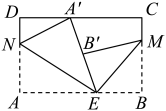$∠ A E N = 32 °$ ， $∠ M E B^{'}$ 的度数为．

查看试题解析

三、解答题

21. 计算：

(1)、 $(- 5) \times (- 7) \times 2$ ；

(2)、 $- 1^{4} + (- 2) \div (- \frac{1}{3}) - | - 9 |$ ．

(3)、 $(\frac{2}{3} - \frac{1}{4} + \frac{1}{6}) \times (- 24)$ ；

(4)、 $(3 x^{2} + 4 - 5 x^{3}) - (x^{3} - 3 + 3 x^{2})$ ．

查看试题解析
22. 先化简，再求值， $2 (3 a b^{2} - a^{3} b) - 3 (2 a b^{2} - a^{3} b)$ ，其中 $a = - \frac{1}{2}$ ， $b = 4$ ．

查看试题解析
23. 如图，在 $9 \times 6$ 的正方形网格中，每个小正方形的顶点都称为格点，点A、B、C都在格点上．

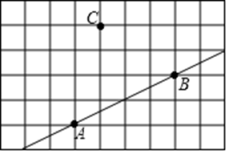(1)、画射线 $A C$ ；

(2)、找一格点D，使得直线 $C D ∥ A B$ ，画出直线 $C D$ ；

(3)、找一格点E，使得直线 $C E ⊥ A B$ 于点H，画出直线 $C E$ ，并注明垂足H．

查看试题解析
24. 如图，长方形的长为 $a$ ，宽为 $2 b$ ．

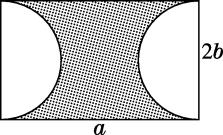(1)、用含 $a ， b$ 的式子表示图中阴影部分的面积 $S$ ；

(2)、当 $a = 5 ， b = 2$ 时，求阴影部分的面积 $S$ 的值（结果保留π）．

查看试题解析
25. 阅读理解，补全证明过程及推理依据.
已知：如图，点E在直线DF上，点B在直线AC上，∠1＝∠2，∠3＝∠4.

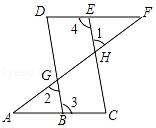
求证∠A＝∠F

证明：∵∠1＝∠2（已知）

∠2＝∠DGF（   ）

∴∠1＝∠DGF（等量代换）

∴ ▲ ∥▲ （   ）

∴∠3+∠▲ ＝180°（   ）

又∵∠3＝∠4（已知）

∴∠4+∠C＝180°（等量代换）

∴ ▲ ∥▲ （   ）

∴∠A＝∠F（   ）

查看试题解析
26. 【感知】如图①，一个点从数轴上原点开始，先向右移动3个单位长度，再向左移动5个单位长度．可以看出，终点表示数-2．

(1)、【应用】点A表示数-3，点M从点A开始，先向右移动10个单位长度，再向左移动15个单位长度，此时点M表示的数；A、M两点距离为．

(2)、【拓展】点B表示数b，点N从点B开始，先向右移动m（m＞0）个单位长度，再向左移动n（n＞0）个单位长度，此时点N表示的数为；B、N两点距离为．

(3)、【探究】如图②，点C表示数-5，D表示数4．点P从点C出发，以每秒2个单位长度的速度向右移动：与此同时，点Q从点D出发，以每秒1个单位长度的速度向左移动，设点P的运动时间为t（t＞0）秒．

①用含t的代数式表示点P和点Q表示的数；

②求点P、Q表示的数相同时t的值；

③求t＝1和t＝4时P、Q两点的距离；

④用含t的代数式表示P、Q两点的距离．

查看试题解析