吉林省吉林市丰满区2022-2023学年七年级上学期期末考试数学试题
试卷更新日期:2023-01-06 类型:期末考试
一、单选题
-
1. 下列各数中,比-3小的数是( )A、3 B、-4 C、0 D、-12. 太阳的半径约为696000千米,用科学记数法表示696000为( )A、69.6×104 B、6.96×105 C、6.96×106 D、0.696×1073. 某正方体的每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“有”字所在面相对的面上的汉字是( )
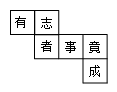 A、者 B、事 C、竟 D、成4. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方--九宫图.请同学们在数字1,2,3,4,5,6,7,8,9中选择合适的数字填入如图所示的幻方中,要求每一横行、同一竖行、两条斜对角线上的数字之和都是15,则n的值为( )
A、者 B、事 C、竟 D、成4. 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方--九宫图.请同学们在数字1,2,3,4,5,6,7,8,9中选择合适的数字填入如图所示的幻方中,要求每一横行、同一竖行、两条斜对角线上的数字之和都是15,则n的值为( )7
2
n
5
A、1 B、2 C、8 D、95. 如图所示,数轴上点 , 对应的有理数分别为 , , 下列说法中正确的是( )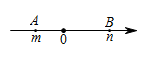 A、 B、 C、 D、6. 一艘船从甲码头到乙码头顺流而行,用了;从乙码头返回甲码头逆流而行,用了 . 已知水流的速度是 , 设船在静水中的平均速度为 , 则可列方程为( )A、 B、 C、 D、
A、 B、 C、 D、6. 一艘船从甲码头到乙码头顺流而行,用了;从乙码头返回甲码头逆流而行,用了 . 已知水流的速度是 , 设船在静水中的平均速度为 , 则可列方程为( )A、 B、 C、 D、二、填空题
-
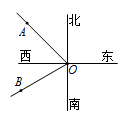
7. 设a是最小的正整数,b是最大的负整数,则 .8. 如果代数式与代数式的值互为相反数,则x= .9. 若一个角等于 , 则这个角的余角度数等于 .10. 如图,在灯塔O处观测到轮船A位于它的西北方向,同时发现轮船B位于它的南偏西的方向上,那么的大小为 .
 11. 任意写出一个含有字母m,n的三次四项式,其中最高次项的系数为6,常数项为-8的式子为 .12. 若一个角的补角是其余角的3倍,则这个角的度数为 .13. 某地区秋季中学生足球联赛,第一阶段分组循环,每队均赛15场,胜一场得3分,平一场得1分,负一场得0分,前进中学足球队的胜场数是负场数的2倍,结果得了21分,则该足球队平的场数为 .14. 如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第个图中小正方形的个数是 . (用含的式子表示)
11. 任意写出一个含有字母m,n的三次四项式,其中最高次项的系数为6,常数项为-8的式子为 .12. 若一个角的补角是其余角的3倍,则这个角的度数为 .13. 某地区秋季中学生足球联赛,第一阶段分组循环,每队均赛15场,胜一场得3分,平一场得1分,负一场得0分,前进中学足球队的胜场数是负场数的2倍,结果得了21分,则该足球队平的场数为 .14. 如图,用相同的小正方形按照某种规律进行摆放.根据图中小正方形的排列规律,猜想第个图中小正方形的个数是 . (用含的式子表示)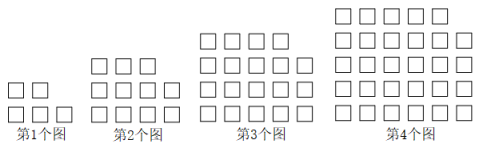
三、解答题
-
15. 计算: .16. 计算: .17. 解方程: .18. 先化简,再求值: , 其中m,n的取值如图所示.
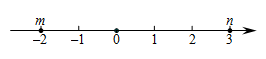 19. 一项工程,由甲工程队单独做需要12天完成,由乙工程队单独做需要24天完成,若由甲、乙两个工程队共同做4天后,剩余工程由甲工程队单独完成,求还需要多少天?20. 历史上的数学巨人欧拉最先把关于x的多项式用记号来表示,把x等于某数m时的多项式的值用来表示.例如,对于多项式 , 当时,多项式的值为 , 若 , 求的值.21. 如图,将边长为m的正方形纸板,沿虚线剪成两个正方形和两个长方形纸板,拿掉边长为的大正方形纸板后,将剩下的三个纸板拼成一个新的长方形纸板.
19. 一项工程,由甲工程队单独做需要12天完成,由乙工程队单独做需要24天完成,若由甲、乙两个工程队共同做4天后,剩余工程由甲工程队单独完成,求还需要多少天?20. 历史上的数学巨人欧拉最先把关于x的多项式用记号来表示,把x等于某数m时的多项式的值用来表示.例如,对于多项式 , 当时,多项式的值为 , 若 , 求的值.21. 如图,将边长为m的正方形纸板,沿虚线剪成两个正方形和两个长方形纸板,拿掉边长为的大正方形纸板后,将剩下的三个纸板拼成一个新的长方形纸板.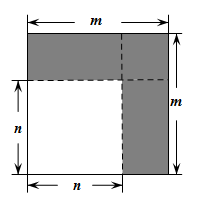 (1)、求拼成的新的长方形纸板的周长;(用含或的代数式表示)(2)、当 , 时,直接写出拼成的新的长方形纸板的面积为 .22. 对于任意四个有理数m,n,d,f,可以组成两个有理数对与 . 我们规定: , . 根据上述规定解决下列问题:(1)、有理数对;(2)、若有理数对 , 求x的值.23. 平面上有四个点 , 按照以下要求作图(保留作图痕迹):
(1)、求拼成的新的长方形纸板的周长;(用含或的代数式表示)(2)、当 , 时,直接写出拼成的新的长方形纸板的面积为 .22. 对于任意四个有理数m,n,d,f,可以组成两个有理数对与 . 我们规定: , . 根据上述规定解决下列问题:(1)、有理数对;(2)、若有理数对 , 求x的值.23. 平面上有四个点 , 按照以下要求作图(保留作图痕迹):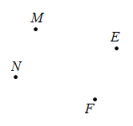 (1)、连接 , 并延长至G,使;(2)、作射线;(3)、作直线 , 并在直线MF上确定点H,使得最短.24. 如图,O为直线上一点, , 平分 , .
(1)、连接 , 并延长至G,使;(2)、作射线;(3)、作直线 , 并在直线MF上确定点H,使得最短.24. 如图,O为直线上一点, , 平分 , .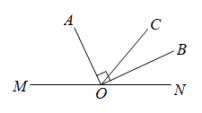 (1)、填空: =;(2)、求的度数;(3)、试判断是否平分 , 并说明理由.25. 甲、乙两家粮油超市以相同价格出售同样的粮油,为了吸引更多的顾客,各自推出不同的优惠方案:在甲超市一次累计购买粮油超出350元之后,超出部分按原价的8折优惠;在乙超市一次累计购买粮油超出260元之后,超出部分按原价的折优惠.设某顾客一次累计购买粮油x元.(1)、请帮助该顾客求出她在甲、乙两家粮油超市购买粮油预计所需支付的费用;(用含x的代数式表示)(2)、当该顾客一次累计购买粮油的原价为380元时,她在哪家粮油超市购买粮油比较合算?请说明理由.26. 如图,在数轴上有三个点 , , , 是原点,满足个单位长度.动点从点出发沿数轴向右以每秒2个单位长度的速度匀速运动;同时动点Q从点出发沿数轴向左匀速运动,速度为单位长度/秒.设点的运动时间为秒.
(1)、填空: =;(2)、求的度数;(3)、试判断是否平分 , 并说明理由.25. 甲、乙两家粮油超市以相同价格出售同样的粮油,为了吸引更多的顾客,各自推出不同的优惠方案:在甲超市一次累计购买粮油超出350元之后,超出部分按原价的8折优惠;在乙超市一次累计购买粮油超出260元之后,超出部分按原价的折优惠.设某顾客一次累计购买粮油x元.(1)、请帮助该顾客求出她在甲、乙两家粮油超市购买粮油预计所需支付的费用;(用含x的代数式表示)(2)、当该顾客一次累计购买粮油的原价为380元时,她在哪家粮油超市购买粮油比较合算?请说明理由.26. 如图,在数轴上有三个点 , , , 是原点,满足个单位长度.动点从点出发沿数轴向右以每秒2个单位长度的速度匀速运动;同时动点Q从点出发沿数轴向左匀速运动,速度为单位长度/秒.设点的运动时间为秒. (1)、当点运动到点时,;(2)、若 , 当点和点相遇时,;(3)、若 , 当 , 两点距离为16个单位长度时,求的值.
(1)、当点运动到点时,;(2)、若 , 当点和点相遇时,;(3)、若 , 当 , 两点距离为16个单位长度时,求的值.