华师大版备考2023中考数学二轮复习 专题23 多边形与平行四边形
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 八边形的外角和是( )A、360° B、720° C、1080° D、1440°2. 如图,点G为的重心,连接并延长分别交于点E,F.连接 , 若.则的长度为( )
 A、1.6 B、1.8 C、2.2 D、2.43. 如图,在中, , 平分交于点D,点F在上,且 , 连接 , E为的中点,连接 , 则的长为( )
A、1.6 B、1.8 C、2.2 D、2.43. 如图,在中, , 平分交于点D,点F在上,且 , 连接 , E为的中点,连接 , 则的长为( ) A、2 B、3 C、4 D、54. 如图,在中,点是边的中点,交对角线于点 , 如果 , 那么的面积为( )
A、2 B、3 C、4 D、54. 如图,在中,点是边的中点,交对角线于点 , 如果 , 那么的面积为( ) A、6 B、12 C、24 D、365. n 边形的每个外角都为 15°,则边数 n 为( )A、20 B、22 C、24 D、266. 如图,在中,点E是边上的点,线段与交于点F,如果 , 那么的长是( )
A、6 B、12 C、24 D、365. n 边形的每个外角都为 15°,则边数 n 为( )A、20 B、22 C、24 D、266. 如图,在中,点E是边上的点,线段与交于点F,如果 , 那么的长是( ) A、3 B、6 C、9 D、127. 如图,在▱ABCD中,Q是CD上的点,AQ交BD于点P,交BC的延长线于点R,若DQ:CQ=3:1,则AP:PR=( )
A、3 B、6 C、9 D、127. 如图,在▱ABCD中,Q是CD上的点,AQ交BD于点P,交BC的延长线于点R,若DQ:CQ=3:1,则AP:PR=( ) A、4:3 B、4:7 C、3:4 D、3:78. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )
A、4:3 B、4:7 C、3:4 D、3:78. 如图,在中,是的平分线,是外角的平分线,于点E,于点D,连接 . 若 , , , 则的长是( )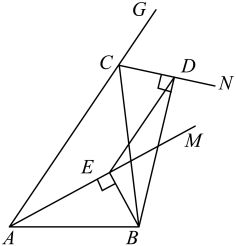 A、 B、 C、 D、9. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )
A、 B、 C、 D、9. 如图,在 中, , , 分别是 , 的中点, , 为 上的点,连接 , .若 cm, cm, cm,则图中阴影部分面积为( )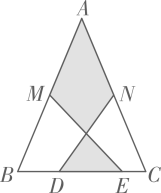 A、25cm2 B、35cm2 C、30cm2 D、42cm210. 如图, ▱ ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°, , 连接OE.下列结论:①∠ADO=30°;②S ▱ ABCD=AB·AC;③OB=AB;④S四边形OECD=S△AOD , 其中成立的个数为( )
A、25cm2 B、35cm2 C、30cm2 D、42cm210. 如图, ▱ ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°, , 连接OE.下列结论:①∠ADO=30°;②S ▱ ABCD=AB·AC;③OB=AB;④S四边形OECD=S△AOD , 其中成立的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,点、分别是、的中点,则 .
 12. 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=4,BC=7,则EF的长为
12. 如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°.若AB=4,BC=7,则EF的长为 13. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
13. 如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当 , 且时,四边形是正方形.
其中正确结论有(填上所有正确结论的序号).
 14. 如图,已知在平行四边形中,点E在边上,射线交的延长线于点F, , , 那么的长为 .
14. 如图,已知在平行四边形中,点E在边上,射线交的延长线于点F, , , 那么的长为 . 15. 如图,在平行四边形ABCD中, , , 的平分线交BC于点E,交DC的延长线于点F,于点G,若 , 则的周长为 .
15. 如图,在平行四边形ABCD中, , , 的平分线交BC于点E,交DC的延长线于点F,于点G,若 , 则的周长为 . 16. 如图,在中,对角线与相交于点 , 延长至点E,使得 , 连接交于点 , 连接 . 下列结论:①;②平分;③以点A,C,E,D为顶点构成的四边形是平行四边形;④ . 其中正确的是(填写所有正确结论的序号).
16. 如图,在中,对角线与相交于点 , 延长至点E,使得 , 连接交于点 , 连接 . 下列结论:①;②平分;③以点A,C,E,D为顶点构成的四边形是平行四边形;④ . 其中正确的是(填写所有正确结论的序号). 17. 如图,在ABC中, , , AD平分交BC于点D,P为直线AB上一动点.连接DP,以DP、DB为邻边构造平行四边形DPQB,连接CQ,若 . 则CQ的最小值为 .
17. 如图,在ABC中, , , AD平分交BC于点D,P为直线AB上一动点.连接DP,以DP、DB为邻边构造平行四边形DPQB,连接CQ,若 . 则CQ的最小值为 .
三、作图题
-
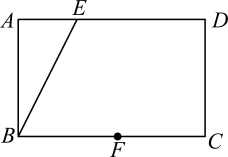
18. 如图,在矩形中,F是边上的一点,请在边上求作一点H,连接 , 使得四边形为平行四边形.(保留作图痕迹,不写作法)
四、解答题
-
19. 如图所示,在▱中,点 , 是对角线上的两点,且 , 连接 , , , 求证:四边形是平行四边形.
 20. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长.
20. 如图,在中,已知 , , 平分 , 于点 , 为中点.求的长. 21. 如图,在中, , 、分别是、的中点,试判断四边形的形状,并证明之.
21. 如图,在中, , 、分别是、的中点,试判断四边形的形状,并证明之.
五、综合题
-


