华师大版备考2023中考数学二轮复习 专题24 特殊的平行四边形
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 如图,所有阴影部分的四边形都是正方形,所有三角形都是直角三角形,若正方形A,B,C的面积依次为4,8,6,则正方形D的面积为( )
 A、10 B、12 C、16 D、182. 如图,点E是、的斜边的中点, , , 则的度数是( )
A、10 B、12 C、16 D、182. 如图,点E是、的斜边的中点, , , 则的度数是( ) A、 B、 C、 D、3. 如图所示,面积为5的正方形的顶点在数轴上,且点表示的数为1,若点在数轴上点在点左侧 , 且 , 则点所表示的数为( )
A、 B、 C、 D、3. 如图所示,面积为5的正方形的顶点在数轴上,且点表示的数为1,若点在数轴上点在点左侧 , 且 , 则点所表示的数为( )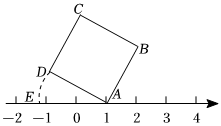 A、 B、 C、 D、4. 如图,大正方形与小正方形的面积之差是50,则阴影部分的面积是( )
A、 B、 C、 D、4. 如图,大正方形与小正方形的面积之差是50,则阴影部分的面积是( ) A、12.5 B、25 C、50 D、1005. 如图,四边形为矩形,AB = 3,BC = 4.点P是线段上一动点,点M为线段AP上一点. , 则的最小值为( )
A、12.5 B、25 C、50 D、1005. 如图,四边形为矩形,AB = 3,BC = 4.点P是线段上一动点,点M为线段AP上一点. , 则的最小值为( )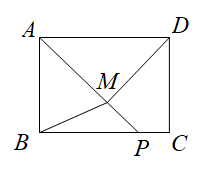 A、 B、 C、 D、6. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图以直角三角形的各边为边分别向同侧作正方形,若知道图中阻影部分的面积之和,则一定能求出( )
A、 B、 C、 D、6. 勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载,如图以直角三角形的各边为边分别向同侧作正方形,若知道图中阻影部分的面积之和,则一定能求出( ) A、正方形的面积 B、正方形的面积 C、正方形的面积 D、的面积7. 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD,若∠BAD=58°,则∠EBD的度数为( )度.
A、正方形的面积 B、正方形的面积 C、正方形的面积 D、的面积7. 如图,在四边形ABCD中,∠ABC=∠ADC=90°,E为对角线AC的中点,连接BE,ED,BD,若∠BAD=58°,则∠EBD的度数为( )度. A、29 B、32 C、45 D、648. 如图,正方形中,分别在边上,相交于点G, 若 , 则 的值是( )
A、29 B、32 C、45 D、648. 如图,正方形中,分别在边上,相交于点G, 若 , 则 的值是( ) A、 B、 C、 D、9. 三国时期的赵爽利用图1证明了勾股定理,后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中,E,B,F在同一条直线上,四边形ABCD,EFGA,HGDJ都是正方形,若正方形ABCD的面积等于100,△IJD面积等于 , 且已知AH=2,则△KCD的面积等于( )
A、 B、 C、 D、9. 三国时期的赵爽利用图1证明了勾股定理,后来日本的数学家关孝和在“赵爽弦图”的启发下利用图2也证明了勾股定理.在图2中,E,B,F在同一条直线上,四边形ABCD,EFGA,HGDJ都是正方形,若正方形ABCD的面积等于100,△IJD面积等于 , 且已知AH=2,则△KCD的面积等于( ) A、 B、39 C、 D、5210. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
A、 B、39 C、 D、5210. 如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )①BF=CF;②若BE⊥AC,则CF=DF;③若BE平分∠ABC,则FG=;④连结EF,若BE⊥AC,则∠DFE=2∠ABE.
 A、①②③ B、③④ C、①②④ D、①②③④
A、①②③ B、③④ C、①②④ D、①②③④二、填空题
-
11. 如图所示,A、B、C、D为矩形的四个顶点, , , 动点P、Q分别从点A、C同时出发,点P以的速度向B移动,一直到达B为止;点Q以的速度向D移动.当P、Q两点从出发开始秒时,点P和点Q的距离是 . (若一点到达终点,另一点也随之停止运动)
 12. 如图,矩形中,、分别是边、上的点,将矩形沿直线翻折后,点落在边上的点处,如果 , , , 那么的长为 .
12. 如图,矩形中,、分别是边、上的点,将矩形沿直线翻折后,点落在边上的点处,如果 , , , 那么的长为 .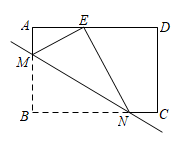 13. 如图,已知 , 且为的中点,连结 , , 当 , 则的度数为.
13. 如图,已知 , 且为的中点,连结 , , 当 , 则的度数为. 14. 如图,一根长的木杆斜靠在竖直的墙上,这时到墙底端的距离为 , 木杆的顶端沿墙面下滑 , 那么点将向外移动;木杆在下滑过程中,面积最大为 .
14. 如图,一根长的木杆斜靠在竖直的墙上,这时到墙底端的距离为 , 木杆的顶端沿墙面下滑 , 那么点将向外移动;木杆在下滑过程中,面积最大为 . 15. 如图.已知在长方形ABCD中,AB=6,BC=8,点E,F分别在边AD,BC上,连结BD,BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在BD上的G,H处,连结CG,则四边形CGHF的周长为.
15. 如图.已知在长方形ABCD中,AB=6,BC=8,点E,F分别在边AD,BC上,连结BD,BE,DF.将△ABE沿BE翻折,将△DCF沿DF翻折,若翻折后,点A,C分别落在BD上的G,H处,连结CG,则四边形CGHF的周长为.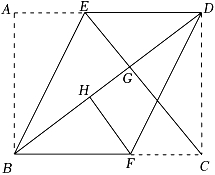 16. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , . 若 , 则度.
16. 如图是一张矩形纸片 , 点是对角线的中点,点在边上,把沿直线折叠,使点落在对角线上的点处,连接 , . 若 , 则度.
三、作图题
-
17. 在的网格中,设每一个小方格的边长为1个单位,画出4个不同的正方形用阴影部分表示 , 所画正方形的顶点都在方格的顶点上,且面积均小于9,并写出相应正方形的边长.
四、解答题
-
18. 如图,菱形的两条对角线相交于点O,若 , 求菱形的周长.
 19. 如图,在△ABC中,∠ABC=45°,AB= , AC=8,BC>6,点E,F分别在BC,AC边上,且AF=CE,求AE+BF的最小值.
19. 如图,在△ABC中,∠ABC=45°,AB= , AC=8,BC>6,点E,F分别在BC,AC边上,且AF=CE,求AE+BF的最小值. 20. 如图,在菱形中,点E是边上一点,延长至点F,使 , 连接 . 求证: .
20. 如图,在菱形中,点E是边上一点,延长至点F,使 , 连接 . 求证: . 21. 如图,四边形是菱形,于点E,于点F.求证: .
21. 如图,四边形是菱形,于点E,于点F.求证: .
五、综合题
-
22. 综合与探究
问题呈现:
“智慧”数学小组在课外数学活动中研究了一个问题,请帮他们解决,如图1,在正方形的边上任取一点E,以为边在与正方形的同侧作正方形 .
(1)、探究结论:
连接 , 则与的数量关系是 , 位置关系是.
(2)、探究发现:如图2,在图1的基础上连接 , , 作的中点M,连接 , 判断与的数量关系和位置关系,并证明你的结论;
(3)、探究拓展:“智慧”数学小组把“边上任取一点E”改成了“边的延长线上任取一点E”,其余条件不变,请在图3中补全图形,并直接写出(2)中的结论是否符合题意,若不符合题意,请直接写出正确的结论.
23. 在矩形中, , , P是射线上的一个动点,作 , 交射线于点E,射线交射线于点F,设 , . (1)、当时,求的长;(2)、如图,当点P在边上时(点P与点B、C不重合),求y关于x的函数关系式,并写出它的定义域;(3)、当时,求的长.24. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D.
(1)、当时,求的长;(2)、如图,当点P在边上时(点P与点B、C不重合),求y关于x的函数关系式,并写出它的定义域;(3)、当时,求的长.24. 将矩形纸片放在平面直角坐标系中,点 , 点 , 点 . 现绕点O顺时针旋转矩形纸片 , 得到新的矩形 , 其中A,B,C的对应点分别为 . 当直线与直线有交点时,设交点为D. (1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.
(1)、在旋转过程中,判断线段和的数量关系,并以图①为例说明理由;(2)、在旋转过程中,当点落在线段上时(如图②),直接写出点的坐标;(3)、在旋转过程中,若线段恰好过线段中点E时(如图③),求线段的长;(4)、在旋转过程中,当线段与线段的交点M恰好是线段中点时(如图④),请直接写出点M和点D的坐标.
-