华师大版备考2023中考数学二轮复习专题19 等腰三角形、等边三角形、直角三角形

试卷更新日期：2023-01-06 类型：二轮复习

进入出卷网下载

一、单选题

1. 有一直角三角形纸片，∠C＝90°BC＝6，AC＝8，现将△ABC按如图那样折叠，使点A与点B重合，折痕为DE，则CE的长为（）

A、 $2 \sqrt{7}$ B、 $\frac{7}{4}$ C、 $\frac{7}{2}$ D、4

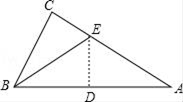查看试题解析
2. 如图：AB是⊙O的直径，弦CD⊥AB于E，若AB＝20，CD＝16，则线段BE的长为（）

A、4 B、6 C、8 D、10

查看试题解析
3. 下列四组数据中，不能作为直角三角形的三边长的是（）

A、7，24，25 B、8，15，17 C、5，11，12 D、3，4，5

查看试题解析
4. 等腰三角形的一个外角是70°，则它的顶角的度数为（）

A、70° B、70°或40° C、110° D、110°或40°

查看试题解析
5. 如图，△ABD和△CBD，∠ADB=90°，∠ABD=∠DBC，AD=DC=1，若AB=4，则BC的长为（）

A、 $\frac{5}{2}$ B、2 $\sqrt{2}$ C、3 D、 $\frac{7}{2}$

查看试题解析
6. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把最小的一个正方形按图2的方式放入较大的正方形内，然后把最大的正方形沿BC翻折，记△EHP和正方形ADNM的面积分别为S₁ ， S₂ ．若点N，M，G三点共线，且满足S₁+S₂ =7，则图2中阴影部分的面积为（）

A、 $\frac{49}{5}$ B、 $\frac{51}{5}$ C、 $\frac{54}{5}$ D、 $\frac{56}{5}$

查看试题解析
7. 如图， $⊙ O$ 为正方形 $A B C D$ 的外接圆，若 $B C = 2$ ，则 $⊙ O$ 的面积为（）

A、 $2 π$ B、 $3 π$ C、 $4 π$ D、 $8 π$

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ，以顶点 $A$ 为圆心， $A C$ 长为半径画弧，交 $A B$ 边于点 $D$ ，再分别以点 $C$ ， $D$ 为圆心，适当的长度为半径画弧，两弧交于点 $E$ ，作射线 $A E$ 交 $B C$ 边于点 $F$ ，点 $P$ 为边 $A B$ 上的动点，若 $B C = 3$ ，则 $P F$ 的取值范围是（）

A、 $\frac{1}{2} \leq P F \leq \frac{3}{2}$ B、 $1 \leq P F \leq 2$ C、 $\frac{3}{2} \leq P F \leq \frac{5}{2}$ D、 $2 \leq P F \leq 3$

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ C = 90 ° ， ∠ A B C = 60 ° ， B C = 6$ ，点O为 $A C$ 中点，点D为线段 $A B$ 上的动点，连接 $O D$ ，设 $B D ＝ x ， O D^{2} ＝ y$ ，则y与x之间的函数关系图象大致为（　　）

A、 B、 C、 D、

查看试题解析
10. 如图，等边 $△ ABC$ 中， $D$ 、 $E$ 分别为 $AC$ 、 $BC$ 边上的点， $AD = CE$ ，连接 $AE$ 、 $BD$ 交于点 $F$ ， $∠ CBD$ 、 $∠ AEC$ 的平分线交于 $AC$ 边上的点 $G$ ， $BG$ 与 $AE$ 交于点 $H$ ，连接 $FG .$ 下列说法： $① △ ABD$ ≌ $△ CAE$ ； $② ∠ BGE = 30 °$ ； $③ ∠ ABG = ∠ BGF$ ； $④ AB = AH + FG$ ；其中正确的说法有（）

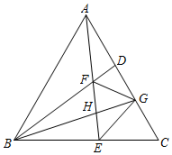A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 已知 $⊙ O$ 的半径为 $5$ ， $A B$ 与 $C D$ 是 $⊙ O$ 的两条弦， $A B = 6$ ， $C D = 8$ ，且 $A B ∥ C D$ ，则 $A C =$ ．

查看试题解析
12. 如图， $D E$ 是 $△ A B C$ 的边 $A C$ 的垂直平分线，垂足为点E，交 $A B$ 于点D，连接 $C D$ ， $∠ B = 30 °$ ， $C D ⊥ B C$ ， $C D = 3$ ，则 $A B$ 的长为.

查看试题解析
13. 如图，在 $△ A B C$ 中， $∠ A = 45 °$ ， $A C = 4$ ， $A B = 5$ ，点 $M$ 为 $A C$ 上动点， $N$ 为 $A B$ 上一点，且 $M N = 3$ ，当点 $M$ 从点 $A$ 运动到点 $C$ 时，则点 $N$ 运动的路程为.

查看试题解析
14. 如图，已知 $△ A B C$ 中， $A B = A C$ ， $A D$ 平分 $∠ B A C$ ，点 $E$ 是 $A B$ 的中点，若 $A C = 6$ ，则 $D E$ 的长为.

查看试题解析
15. 如图， $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 4$ ， $B C = 3$ ，点 $P$ 为 $A C$ 边上的动点，过点 $P$ 作 $P D ⊥ A B$ 于点 $D$ ，则 $P B + P D$ 的最小值为.

查看试题解析
16. 如图，正方形 $A B C D$ 的边长为4，点 $E ， F$ 分别在 $B C ， B D$ 上，且 $B E = 1$ ，过三点 $C ， E ， F$ 作 $⊙ O$ 交 $C D$ 于点G.在点F整个运动过程中，当 $E F ， F G ， C G$ 中满足某两条线段相等时， $B F$ 的长为.

查看试题解析
17. 如图， $△ A B C$ 与 $△ A D E$ 都是等边三角形， $B D$ 和 $C E$ 相交于点 $P$ ，连接 $A P ．$ 下面结论中， $① B D = C E$ ； $② ∠ E P D = 60 °$ ； $③ P A$ 不是 $∠ B P E$ 的平分线； $④ P E = P A + P D ．$ 所有正确结论的序号是．

查看试题解析

三、作图题

18. 如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形：

(1)、在图（1）中，画一个等腰三角形，使它的面积等于6；

(2)、在图（2）中，画一个直角三角形，使它的三边长都是有理数；

查看试题解析

四、解答题

19. 如图，在三角形ABC中，AB＝AC，∠C＝25°，点D在线段CA的延长线上，且DA＝AC，求∠ABD的度数.

查看试题解析
20. 为庆祝中华人民共和国成立73周年，喜迎党的二十大胜利召开，学校组织了“献礼二十大”小制作展示活动．小彬计划制作一架飞机模型，如图的四边形材料是飞机垂直尾翼的雏形．小彬测量发现 $A B = 25 c m$ ， $B C = 18 c m$ ， $A D = 7 c m$ ， $C D = 30 c m$ ．根据设计要求，还需保证 $A D ∥ B C$ ．由于手头工具有限，小彬只能测得 $B D = 24 c m$ ．根据以上数据，请你判断该材料是否符合设计要求，并说明理由．

查看试题解析
21. 如图，在四边形ABCD中，AB=AD=8cm，∠A=60°，∠ADC=150°，已知四边形ABCD的周长为32cm，求△BCD的面积．

查看试题解析
22. 如图，已知锐角三角形 $A B C$ 的两条高 $B E ， C D$ 相交于点O，且 $O B = O C$ ．请你判断 $△ A B C$ 的形状，并说明理由．

查看试题解析

五、综合题

23. 如图，△ABC是⊙O的内接三角形，AC＝BC，D为⊙O的弧AB上一点，延长DA至点E，使CE＝CD.

(1)、求证：AE＝BD；

(2)、若AC⊥BC，试说明AD、BD与CD之间是否存在某种确定的等量关系？请画图（非尺规作图），写出你的结论并证明.

(3)、若AD+BD＝ $\sqrt{3}$ CD，则∠ACB＝.

查看试题解析
24. 定义：若连结三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形，我们称这条线段为该三角形的智慧线，这个三角形叫做智慧三角形.

(1)、如图1，在智慧三角形ABC中，AD⊥BC，AD为该三角形的智慧线，CD＝1，AC＝2，则BD长为， ∠B的度数为.

(2)、如图2，△ABC为等腰直角三角形，∠BAC＝90°，F是斜边BC延长线上一点，连结AF，以AF为直角边作等腰直角三角形AFE（点A，F，E按顺时针排列），∠EAF＝90°，AE交BC于点D，连结EC，EB.当∠BDE＝2∠BCE时，求证：ED是△EBC的智慧线.

(3)、如图3，△ABC中，AB＝AC＝5，BC²＝80.若△BCD是智慧三角形，且AC为智慧线，求△BCD的面积.

查看试题解析
25. 如图1，直线 $y = - m x + 4 m (m > 1)$ 交x轴于点A，交y轴于点B，点C在 $O B$ 上，且 $∠ O A C = 45 °$ ．

(1)、直接写出点C的坐标为；

(2)、P为x轴负半轴上一点，且 $O P = 2 B C$ ，连接 $P B$ ，设 $△ P A B$ 的面积为S，直接写出S与m的函数关系式；

(3)、在（2）的条件下，过点B作 $B D ⊥ P B$ ，交x轴于点D，若 $B D + A D = P A$ ，求点D的坐标．

查看试题解析

华师大版备考2023中考数学二轮复习 专题19 等腰三角形、等边三角形、直角三角形

一、单选题

二、填空题

三、作图题

四、解答题

五、综合题

华师大版备考2023中考数学二轮复习专题19 等腰三角形、等边三角形、直角三角形