华师大版备考2023中考数学二轮复习 专题18 全等三角形
试卷更新日期:2023-01-06 类型:二轮复习
一、单选题
-
1. 已知三角形的两条边长分别为和 , 则第三条边长可以是( )A、 B、 C、 D、2. 如图, , 给出下列结论:①;②;③;④ . 其中正确的个数是( )
 A、1 B、2 C、3 D、43. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )
A、1 B、2 C、3 D、43. 如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( ) A、71° B、76° C、78° D、80°4. 如图,在中, , 是高,是角平分线,交于点 , 过点作 , 垂足为 , 下面说法中不一定正确的是( )
A、71° B、76° C、78° D、80°4. 如图,在中, , 是高,是角平分线,交于点 , 过点作 , 垂足为 , 下面说法中不一定正确的是( ) A、 B、 C、 D、的周长等于线段的长5. 如图, , 是的高线,与相交于点 . 若 , 则能判断的依据是( )
A、 B、 C、 D、的周长等于线段的长5. 如图, , 是的高线,与相交于点 . 若 , 则能判断的依据是( ) A、 B、 C、 D、6. 根据下列已知条件,能确定的形状和大小的是( )A、 , , B、 , , C、 , , D、 , ,7. 如图,在中, , , 是边上的中线,则的长度可能为( )
A、 B、 C、 D、6. 根据下列已知条件,能确定的形状和大小的是( )A、 , , B、 , , C、 , , D、 , ,7. 如图,在中, , , 是边上的中线,则的长度可能为( )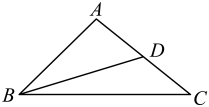 A、1 B、2 C、5 D、88. 如图,点 , , , 在一条直线上, , , 添加下列条件仍不能判断的是( )
A、1 B、2 C、5 D、88. 如图,点 , , , 在一条直线上, , , 添加下列条件仍不能判断的是( ) A、 B、 C、 D、9. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )
A、 B、 C、 D、9. 如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形 , 且四边形的面积是四边形的3倍. 下列选项正确的是( )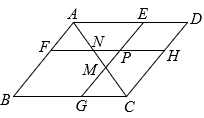 A、 B、 C、 D、10. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )
A、 B、 C、 D、10. 如图,等腰中, , , 于点 , 的平分线分别交、于、两点,为的中点,的延长线交于点 , 连接 , 下列结论:;为等腰三角形;;; , 其中正确结论有( )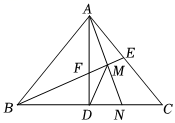 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. △ABC中,AB=AC,∠A=70°,则∠B的度数是度.12. 如图,ΔABC中,点E在AD上,且点E是ΔABC的重心,若=18,则等于。
 13. 如图,在△ABC中,AB=AC=7,AB的垂直平分线DE分别交BC,AB于点D,E,连接AD,若BC=10,则△ACD的周长为 .
13. 如图,在△ABC中,AB=AC=7,AB的垂直平分线DE分别交BC,AB于点D,E,连接AD,若BC=10,则△ACD的周长为 . 14. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=10,点D为斜边AB的中点,点P是直角边BC上一动点,连结AP,DP,则AP+DP的最小值为。
14. 如图,在△ABC中,∠ACB=90°,∠B=30°,AB=10,点D为斜边AB的中点,点P是直角边BC上一动点,连结AP,DP,则AP+DP的最小值为。 15. 如图, , 且∠EAB=120°,∠B=30°,∠CAD=10°,∠CFD=°.
15. 如图, , 且∠EAB=120°,∠B=30°,∠CAD=10°,∠CFD=°. 16. 如图,在中, , , , 点P在的内部(不包括边上),且的面积等于的面积的一半,设点D为的重心,点P、D两点之间的距离为d,那么d的最小值为 .
16. 如图,在中, , , , 点P在的内部(不包括边上),且的面积等于的面积的一半,设点D为的重心,点P、D两点之间的距离为d,那么d的最小值为 . 17. 如图,是等边三角形, , D是的中点,F是直线上一动点,线段绕点D逆时针旋转 , 得到线段 , 当点F运动时,的最小值是 .
17. 如图,是等边三角形, , D是的中点,F是直线上一动点,线段绕点D逆时针旋转 , 得到线段 , 当点F运动时,的最小值是 .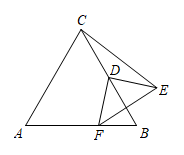
三、作图题
-
18. 如图,中, , .
 (1)、用尺规作的平分线交于点D.(保留作图痕迹,不要求写作法);(2)、求的度数.19. 如图
(1)、用尺规作的平分线交于点D.(保留作图痕迹,不要求写作法);(2)、求的度数.19. 如图 (1)、在图1中,用尺规作AB边的中垂线,交BC于点P.(保留作图痕迹)(2)、如图2,是由边长为1的小正方形拼成的网格,画一个以格点为顶点,斜边长为 的直角三角形(各边均为无理数).
(1)、在图1中,用尺规作AB边的中垂线,交BC于点P.(保留作图痕迹)(2)、如图2,是由边长为1的小正方形拼成的网格,画一个以格点为顶点,斜边长为 的直角三角形(各边均为无理数).四、解答题
-
20. 如图,已知 , , 求证: .
 21. 如图,在中,点D是的中点,过点D作交于点E,连接 . 若的周长为13, , 求的周长.
21. 如图,在中,点D是的中点,过点D作交于点E,连接 . 若的周长为13, , 求的周长.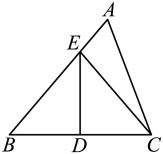 22. 已知:如图,AC=BD,AE=BF,∠A=∠B,求证:△AFC≌△BED.
22. 已知:如图,AC=BD,AE=BF,∠A=∠B,求证:△AFC≌△BED. 23. 如图, , , 求证:.
23. 如图, , , 求证:.
五、综合题
-
24. 如图,△ABC中,AB=BC=AC=6cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边顺时针运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
 (1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间;(3)、点M、N运动几秒后,可得到直角三角形△AMN?25. 如图, , 射线 , 且 , 点是线段不与点、重合上的动点,过点作交射线于点 , 连接.
(1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间;(3)、点M、N运动几秒后,可得到直角三角形△AMN?25. 如图, , 射线 , 且 , 点是线段不与点、重合上的动点,过点作交射线于点 , 连接. (1)、如图1,若 , , 求的长.(2)、如图2,若平分 ,
(1)、如图1,若 , , 求的长.(2)、如图2,若平分 ,试猜测和的数量关系,并说明理由;
若的面积为5,求四边形的面积.
(3)、如图3,①已知点是网格中的格点,若三角形是以为底边的等腰三角形,那么这样的点共有 ▲ 个;
②在网格中找出一个点 , 使得点到点 , 和点 , 的距离分别相等,请在网格中标注点保留作图痕迹
26. 已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,F为BE的中点,连结DF,CF. (1)、如图①,当点D在AB上,点E在AC上,请写出此时线段DF,CF的数量关系和位置关系,并说明理由.(2)、如图②,在(1)的条件下将△ADE绕点A顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.
(1)、如图①,当点D在AB上,点E在AC上,请写出此时线段DF,CF的数量关系和位置关系,并说明理由.(2)、如图②,在(1)的条件下将△ADE绕点A顺时针旋转45°,请你判断此时(1)中的结论是否仍然成立,并证明你的判断.