华师大版备考2023中考数学二轮复习 专题17 线段、角、相交线与平行线
试卷更新日期：2023-01-06 类型：二轮复习
一、单选题
-
1. 如图， ， 点 ， ， 在同一直线上，若 ， ， 则的度数是（ ）
A、 B、 C、 D、2. 如图，平分 ， 于点 ， 若 ， 点是边上一动点，关于线段叙述正确的是（ ）
A、 B、 C、 D、3. 如图，直线 ， 等边的顶点C在直线b上，若 ， 则的度数为（ ）
A、100° B、110° C、120° D、130°4. 如图，将绕点逆时针旋转至 ， 使 ， 若 ， 则旋转角的度数是（ ）
A、 B、 C、 D、5. 如图，在△ABC中，AB＝AC，AD是高线，E是AB的中点，已知△ABC的面积为8，则△ADE的面积为（ ）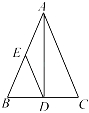
A、1 B、2 C、3 D、46. 如图，于点B，于点E， ， ， ， ， 则的度数为（ ）
A、 B、 C、 D、7. 如图，将△ABC绕点C顺时针旋转得到△EDC，若点A恰好在ED的延长线上，∠BAC＝40°，则∠BAE的度数为（ ）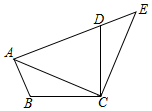
A、80° B、60° C、65° D、70°8. 如图，为线段上一动点不与 ， 重合 ， 在同侧分别作等边和等边 ， 与交于点 ， 与交于点 ， 与交于点 ， 连接 ， 则有以下五个结论：；；；； ．
其中正确的有（ ）
A、①③⑤ B、①③④⑤ C、①②③⑤ D、①②③④⑤二、填空题
-
9. 如图，在中， ， ， 三角形的外角和的平分线交于点E，则 ．
10. 如图，已知 ， E为的中点，若 ， ， 则 ．
11. 如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，如果∠A=40°，则∠1=度.
12. 如图，在△ABC中，AB＝AC，点D、E在BC的延长线上，G是AC上一点，且CG＝CD，F是GD上一点，且DF＝DE．若∠A＝100°，则∠E的大小为度．
13. 一个正n棱柱有18条棱，一条侧棱为 ， 一条底边为 ， 则它的侧面积是 ．14. 如图，把长方形纸条依次沿着线段、折叠，且 ， 得到“Z”字形图案．已知 ， 要使点 ， 点分别在和的延长线上（不与重合），则 ．
15. 如图，已知三内角的角平分线交于点D，三边的垂直平分线交于点E，若 ， 则度．
三、解答题
-
16. 如图，已知点在同一条直线上，且 ， .求证：.
17. 如图，在△ABC中，AB=AC ， BD= CD ， DE⊥AB ， DF⊥AC ， 垂足分别为点E、F ， 求证：DE=DF.
18. 如图，在△ABC中，AC＝BC，CD平分△ABC的外角∠ACE，试说明CD∥AB的理由.
解：∵AC＝BC（已知），
∴∠A＝∠▲ （ ）
∵CD平分∠ACE（已知）
∴∠ACD＝∠ECD（ ）
∵∠ACE＝∠A+∠B（ ）
∴∠ACE＝2∠A，∠ACE＝2∠ACD.
∴∠A＝∠▲ （等量的传递性）.
∴AB∥FE（ ）
四、综合题
-
19. 如图，中， ， 于点 ， ， .
(1)、求 ， 的长；(2)、若点是射线上的一个动点，作于点 ， 连结当点在线段上时，若是以为腰的等腰三角形，请求出所有符合条件的的长.